2-Problema de Satisfacción (2-SAT)

Problema booleano de satisfacción

La Satisfacción Booleana o simplemente SAT es el problema de determinar si una fórmula booleana es satisfactoria o insatisfactoria.

Satisfiable: si a las variables booleanas se les pueden asignar valores tales que la fórmula resulte ser VERDADERA, entonces decimos que la fórmula es satisfacible.
Insatisfactorio: Si no es posible asignar tales valores, entonces decimos que la fórmula es insatisfactoria.

Ejemplos:

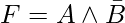$F = A \wedge \bar{B}$ , es satisfactoria, porque A = VERDADERO y B = FALSO hace que F = VERDADERO.
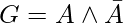$G = A \wedge \bar{A}$ , es insatisfactorio, porque:

$A$	$\bar{A}$	$G$
CIERTO	FALSO	FALSO
FALSO	CIERTO	FALSO

Nota: el problema de satisfacibilidad booleano es NP-completo (para la prueba, consulte el teorema de Cook ).

Boolean Satisfiability Problem

¿Qué es el problema 2-SAT?

2-SAT es un caso especial de Problema de Satisfacción Booleano y se puede resolver
en tiempo polinomial .

Para entender esto mejor, primero veamos qué es la Forma Normal Conjuntiva (CNF) o también conocida como Producto de Sumas (POS).

CNF: CNF es una conjunción (AND) de cláusulas, donde cada cláusula es una disyunción (OR).
Ahora, 2-SAT limita el problema de SAT solo a aquellas fórmulas booleanas que se expresan como un CNF con cada cláusula que tiene solo 2 términos (también llamado 2-CNF ).

Ejemplo: $F = (A_1 \vee B_1) \wedge (A_2 \vee B_2) \wedge (A_3 \vee B_3) \wedge ....... \wedge (A_m \vee B_m)$

Así, el Problema de Satisfacción 2 puede enunciarse como:

Dado CNF con cada cláusula que tiene solo 2 términos, ¿es posible asignar tales valores a las variables para que CNF sea VERDADERO?

Ejemplos:

Entrada: $F = (x1 \vee x2) \wedge (x2 \vee \bar{x1}) \wedge (\bar{x1} \vee \bar{x2})$ Salida: La expresión dada es satisfactoria. (para x1 = FALSO, x2 = VERDADERO) Entrada: $F = (x1 \vee x2) \wedge (x2 \vee \bar{x1}) \wedge (x1 \vee \bar{x2}) \wedge (\bar{x1} \vee \bar{x2})$ Salida: La expresión dada es insatisfactoria. (para todas las combinaciones posibles de x1 y x2)

Enfoque para el problema 2-SAT

Para que el valor CNF sea VERDADERO, el valor de cada cláusula debe ser VERDADERO. Sea una de las cláusulas $(A \vee B)$ . $\text{[math]}$ = VERDADERO

Si A = 0, B debe ser 1, es decir $(\bar{A} \Rightarrow B)$
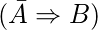
Si B = 0, A debe ser 1, es decir $(\bar{B} \Rightarrow A)$

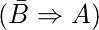
De este modo,

 = TRUE is equivalent to

Ahora, podemos expresar el CNF como una implicación. Entonces, creamos un gráfico de implicación que tiene 2 aristas para cada cláusula del CNF.
$(A \vee B)$ se expresa en el gráfico de implicación como $edge(\bar{A} \rightarrow B) \ & edge(\bar{B} \rightarrow A)$

Por lo tanto, para una fórmula booleana con cláusulas ‘m’, hacemos un gráfico de implicación con:

2 bordes para cada cláusula, es decir, bordes de ‘2m’.
1 Node por cada variable booleana involucrada en la fórmula booleana.

Veamos un ejemplo de gráfico de implicación.
$\text{[math]}$

Approach for 2-SAT Problem

Nota: La implicación (si A entonces B) es equivalente a su contrapositiva (si $\bar{B}$ entonces $\bar{A}$ ).
Ahora, considere los siguientes casos:

CASO 1: Si $edge(X \rightarrow \bar{X})$ [Tex] existe en el gráfico [/Tex] Esto significa que $(X \Rightarrow \bar{X})$ si X = VERDADERO, $\bar{X}$ = VERDADERO, lo cual es una contradicción. Pero si X = FALSO, no hay restricciones de implicación. Por lo tanto, X = FALSO

CASO 2: Si $edge(\bar{X} \rightarrow X)$ [Tex] existe en el gráfico [/Tex] Esto significa que $(\bar{X} \Rightarrow X)$ si $\bar{X}$ = VERDADERO, X = VERDADERO, lo cual es una contradicción. Pero si $\bar{X}$ = FALSO, no hay restricciones de implicación. Por lo tanto, $\bar{X}$ = FALSO, es decir, X = VERDADERO

CASO 3: Si $edge(X \rightarrow \bar{X}) \& edge(\bar{X} \rightarrow X)$ [Tex]ambos existen en el gráfico[/Tex]Un borde requiere que X sea VERDADERO y el otro requiere que X sea FALSO. Por lo tanto, no hay asignación posible en tal caso.

CONCLUSIÓN:

Si dos variables cualesquiera $X$ y $\bar{X}$ están en un ciclo, es decir $path(\bar{A} \rightarrow B) \& path({B} \rightarrow A)$ , ambas existen, entonces el CNF es insatisfactorio. En caso contrario, existe una posible cesión y el CNF es satisfecho.
Tenga en cuenta aquí que usamos ruta debido a la siguiente propiedad de implicación:
si tenemos $(A \Rightarrow B) \& (B \Rightarrow C), then A \Rightarrow C$
Por lo tanto, si tenemos una ruta en el gráfico de implicación, eso es prácticamente lo mismo que tener un borde directo.

CONCLUSIÓN DESDE EL PUNTO DE VISTA DE LA IMPLEMENTACIÓN:

Si tanto X como $\bar{X}$ se encuentran en el mismo SCC (Componente fuertemente conectado), el CNF es insatisfactorio.
Un componente fuertemente conectado de un grafo dirigido tiene Nodes tales que se puede llegar a cada Node desde cualquier otro Node en ese SCC.
Ahora, si X y $\bar{X}$ se encuentran en el mismo SCC, definitivamente tendremos $path(\bar{A} \rightarrow B) \& path({B} \rightarrow A)$ presente y, por lo tanto, la conclusión.
La comprobación del SCC se puede realizar en O(E+V) utilizando el Algoritmo de Kosaraju

Implementación:

C++

// C++ implementation to find if the given
// expression is satisfiable using the
// Kosaraju's Algorithm
#include <bits/stdc++.h>
using namespace std;
  
const int MAX = 100000;
  
// data structures used to implement Kosaraju's
// Algorithm. Please refer
// https://www.geeksforgeeks.org/strongly-connected-components/
vector<int> adj[MAX];
vector<int> adjInv[MAX];
bool visited[MAX];
bool visitedInv[MAX];
stack<int> s;
  
// this array will store the SCC that the
// particular node belongs to
int scc[MAX];
  
// counter maintains the number of the SCC
int counter = 1;
  
// adds edges to form the original graph
void addEdges(int a, int b)
{
    adj[a].push_back(b);
}
  
// add edges to form the inverse graph
void addEdgesInverse(int a, int b)
{
    adjInv[b].push_back(a);
}
  
// for STEP 1 of Kosaraju's Algorithm
void dfsFirst(int u)
{
    if(visited[u])
        return;
  
    visited[u] = 1;
  
    for (int i=0;i<adj[u].size();i++)
        dfsFirst(adj[u][i]);
  
    s.push(u);
}
  
// for STEP 2 of Kosaraju's Algorithm
void dfsSecond(int u)
{
    if(visitedInv[u])
        return;
  
    visitedInv[u] = 1;
  
    for (int i=0;i<adjInv[u].size();i++)
        dfsSecond(adjInv[u][i]);
  
    scc[u] = counter;
}
  
// function to check 2-Satisfiability
void is2Satisfiable(int n, int m, int a[], int b[])
{
    // adding edges to the graph
    for(int i=0;i<m;i++)
    {
        // variable x is mapped to x
        // variable -x is mapped to n+x = n-(-x)
  
        // for a[i] or b[i], addEdges -a[i] -> b[i]
        // AND -b[i] -> a[i]
        if (a[i]>0 && b[i]>0)
        {
            addEdges(a[i]+n, b[i]);
            addEdgesInverse(a[i]+n, b[i]);
            addEdges(b[i]+n, a[i]);
            addEdgesInverse(b[i]+n, a[i]);
        }
  
        else if (a[i]>0 && b[i]<0)
        {
            addEdges(a[i]+n, n-b[i]);
            addEdgesInverse(a[i]+n, n-b[i]);
            addEdges(-b[i], a[i]);
            addEdgesInverse(-b[i], a[i]);
        }
  
        else if (a[i]<0 && b[i]>0)
        {
            addEdges(-a[i], b[i]);
            addEdgesInverse(-a[i], b[i]);
            addEdges(b[i]+n, n-a[i]);
            addEdgesInverse(b[i]+n, n-a[i]);
        }
  
        else
        {
            addEdges(-a[i], n-b[i]);
            addEdgesInverse(-a[i], n-b[i]);
            addEdges(-b[i], n-a[i]);
            addEdgesInverse(-b[i], n-a[i]);
        }
    }
  
    // STEP 1 of Kosaraju's Algorithm which
    // traverses the original graph
    for (int i=1;i<=2*n;i++)
        if (!visited[i])
            dfsFirst(i);
  
    // STEP 2 of Kosaraju's Algorithm which
    // traverses the inverse graph. After this,
    // array scc[] stores the corresponding value
    while (!s.empty())
    {
        int n = s.top();
        s.pop();
  
        if (!visitedInv[n])
        {
            dfsSecond(n);
            counter++;
        }
    }
  
    for (int i=1;i<=n;i++)
    {
        // for any 2 variable x and -x lie in
        // same SCC
        if(scc[i]==scc[i+n])
        {
            cout << "The given expression "
                 "is unsatisfiable." << endl;
            return;
        }
    }
  
    // no such variables x and -x exist which lie
    // in same SCC
    cout << "The given expression is satisfiable."
         << endl;
    return;
}
  
//  Driver function to test above functions
int main()
{
    // n is the number of variables
    // 2n is the total number of nodes
    // m is the number of clauses
    int n = 5, m = 7;
  
    // each clause is of the form a or b
    // for m clauses, we have a[m], b[m]
    // representing a[i] or b[i]
  
    // Note:
    // 1 <= x <= N for an uncomplemented variable x
    // -N <= x <= -1 for a complemented variable x
    // -x is the complement of a variable x
  
    // The CNF being handled is:
    // '+' implies 'OR' and '*' implies 'AND'
    // (x1+x2)*(x2’+x3)*(x1’+x2’)*(x3+x4)*(x3’+x5)*
    // (x4’+x5’)*(x3’+x4)
    int a[] = {1, -2, -1, 3, -3, -4, -3};
    int b[] = {2, 3, -2, 4, 5, -5, 4};
  
    // We have considered the same example for which
    // Implication Graph was made
    is2Satisfiable(n, m, a, b);
  
    return 0;
}

Java

// Java implementation to find if the given 
// expression is satisfiable using the 
// Kosaraju's Algorithm 
import java.io.*;
import java.util.*;
  
class GFG{
  
static final int MAX = 100000;
  
// Data structures used to implement Kosaraju's
// Algorithm. Please refer
// https://www.geeksforgeeks.org/strongly-connected-components/
@SuppressWarnings("unchecked")
static List<List<Integer> > adj = new ArrayList();
  
@SuppressWarnings("unchecked")
static List<List<Integer> > adjInv = new ArrayList();
static boolean[] visited = new boolean[MAX];
static boolean[] visitedInv = new boolean[MAX];
static Stack<Integer> s = new Stack<Integer>();
  
// This array will store the SCC that the
// particular node belongs to
static int[] scc = new int[MAX];
  
// counter maintains the number of the SCC
static int counter = 1;
  
// Adds edges to form the original graph void
static void addEdges(int a, int b)
{
    adj.get(a).add(b);
}
  
// Add edges to form the inverse graph
static void addEdgesInverse(int a, int b)
{
    adjInv.get(b).add(a);
}
  
// For STEP 1 of Kosaraju's Algorithm
static void dfsFirst(int u)
{
    if (visited[u])
        return;
  
    visited[u] = true;
  
    for(int i = 0; i < adj.get(u).size(); i++)
        dfsFirst(adj.get(u).get(i));
  
    s.push(u);
}
  
// For STEP 2 of Kosaraju's Algorithm
static void dfsSecond(int u)
{
    if (visitedInv[u])
        return;
  
    visitedInv[u] = true;
  
    for(int i = 0; i < adjInv.get(u).size(); i++)
        dfsSecond(adjInv.get(u).get(i));
  
    scc[u] = counter;
}
  
// Function to check 2-Satisfiability
static void is2Satisfiable(int n, int m, 
                           int a[], int b[])
{
      
    // Adding edges to the graph
    for(int i = 0; i < m; i++) 
    {
          
        // variable x is mapped to x
        // variable -x is mapped to n+x = n-(-x)
  
        // for a[i] or b[i], addEdges -a[i] -> b[i]
        // AND -b[i] -> a[i]
        if (a[i] > 0 && b[i] > 0) 
        {
            addEdges(a[i] + n, b[i]);
            addEdgesInverse(a[i] + n, b[i]);
            addEdges(b[i] + n, a[i]);
            addEdgesInverse(b[i] + n, a[i]);
        }
  
        else if (a[i] > 0 && b[i] < 0) 
        {
            addEdges(a[i] + n, n - b[i]);
            addEdgesInverse(a[i] + n, n - b[i]);
            addEdges(-b[i], a[i]);
            addEdgesInverse(-b[i], a[i]);
        }
  
        else if (a[i] < 0 && b[i] > 0) 
        {
            addEdges(-a[i], b[i]);
            addEdgesInverse(-a[i], b[i]);
            addEdges(b[i] + n, n - a[i]);
            addEdgesInverse(b[i] + n, n - a[i]);
        }
  
        else
        {
            addEdges(-a[i], n - b[i]);
            addEdgesInverse(-a[i], n - b[i]);
            addEdges(-b[i], n - a[i]);
            addEdgesInverse(-b[i], n - a[i]);
        }
    }
  
    // STEP 1 of Kosaraju's Algorithm which
    // traverses the original graph
    for(int i = 1; i <= 2 * n; i++)
        if (!visited[i])
            dfsFirst(i);
  
    // STEP 2 of Kosaraju's Algorithm which
    // traverses the inverse graph. After this,
    // array scc[] stores the corresponding value
    while (!s.isEmpty()) 
    {
        int top = s.peek();
        s.pop();
  
        if (!visitedInv[top]) 
        {
            dfsSecond(top);
            counter++;
        }
    }
  
    for(int i = 1; i <= n; i++) 
    {
          
        // For any 2 variable x and -x lie in
        // same SCC
        if (scc[i] == scc[i + n])
        {
            System.out.println("The given expression" +
                               "is unsatisfiable.");
            return;
        }
    }
  
    // No such variables x and -x exist which lie
    // in same SCC
    System.out.println("The given expression " + 
                       "is satisfiable.");
}
  
// Driver code
public static void main(String[] args)
{
      
    // n is the number of variables
    // 2n is the total number of nodes
    // m is the number of clauses
    int n = 5, m = 7;
  
    for(int i = 0; i < MAX; i++) 
    {
        adj.add(new ArrayList<Integer>());
        adjInv.add(new ArrayList<Integer>());
    }
  
    // Each clause is of the form a or b
    // for m clauses, we have a[m], b[m]
    // representing a[i] or b[i]
  
    // Note:
    // 1 <= x <= N for an uncomplemented variable x
    // -N <= x <= -1 for a complemented variable x
    // -x is the complement of a variable x
  
    // The CNF being handled is:
    // '+' implies 'OR' and '*' implies 'AND'
    // (x1+x2)*(x2â+x3)*(x1â+x2â)*(x3+x4)*(x3â+x5)*
    // (x4â+x5â)*(x3â+x4)
    int a[] = { 1, -2, -1, 3, -3, -4, -3 };
    int b[] = { 2, 3, -2, 4, 5, -5, 4 };
  
    // We have considered the same example 
    // for which Implication Graph was made
    is2Satisfiable(n, m, a, b);
}
}
  
// This code is contributed by jithin

Producción

The given expression is satisfiable.

Más casos de prueba:

Input : n = 2, m = 3
        a[] = {1, 2, -1}
        b[] = {2, -1, -2}
Output : The given expression is satisfiable.

Input : n = 2, m = 4
        a[] = {1, -1, 1, -1}
        b[] = {2, 2, -2, -2}
Output : The given expression is unsatisfiable.

Este artículo es una contribución de Aanya Jindal . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Problema booleano de satisfacción

¿Qué es el problema 2-SAT?

Enfoque para el problema 2-SAT

C++

Java

Deja una respuesta Cancelar la respuesta