Para dos vectores reales n-dimensionales P y Q, la operación s(P,Q) se define como sigue:
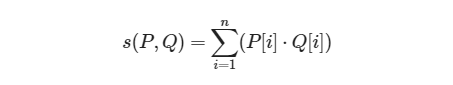
Sea L un conjunto de vectores reales distintos de cero de 10 dimensiones tales que para cada par de vectores distintos P,Q∈L, s(P,Q)=0. ¿Cuál es la cardinalidad máxima posible para el conjunto L?
(A) 9
(B) 10
(C) 11
(D) 100
Respuesta: (B)
Explicación: s(P,Q) es la suma de los productos punto de los vectores P y Q en cada dimensión.
El producto punto 0 indica que los vectores deben ser ortogonales entre sí.
En un espacio de n dimensiones, tenemos n ejes ortogonales entre sí.
Se da que para cada par el producto escalar debe ser 0, entonces como máximo se pueden considerar n vectores cada uno mencionando cada dimensión.
Por lo tanto, para el conjunto de vectores ℒ del espacio de 10 dimensiones, pueden estar presentes 10 vectores ortogonales entre sí.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA