Para ilustrar el proceso de reducción de estado y asignación de estado primero tenemos que conocer los conceptos de diagrama de estado, tabla de estado y ecuación de estado. En este artículo, vamos a aprender todos los temas relacionados con la reducción y asignación de estado.
Diagrama de estado: el gráfico de estado o diagrama de estado es una representación pictórica de las relaciones entre el estado actual, el estado de entrada, el estado siguiente y el estado de salida de un circuito secuencial, es decir, un diagrama de estado es una representación gráfica del comportamiento de un circuito secuencial. .
Ejemplo: considere una tabla de excitación de flip-flop JK
| Q norte | Qn +1 | j | k |
|---|---|---|---|
| 0 | 0 | 0 | X |
| 0 | 1 | 1 | X |
| 1 | 0 | X | 1 |
| 1 | 1 | X | 0 |
El diagrama de estado de la tabla anterior es
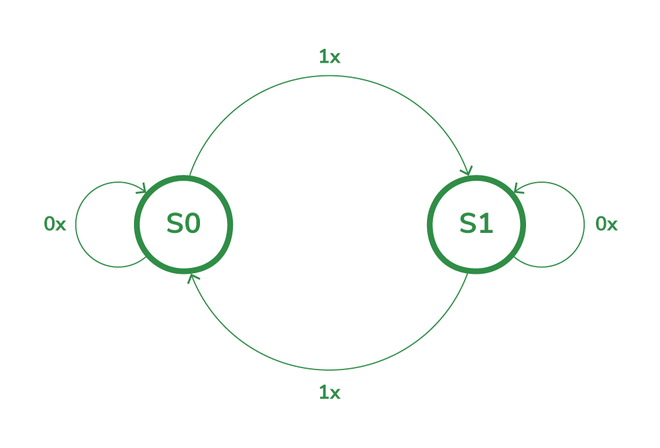
Diagrama de estado del flip-flop JK
Tabla de estados: Si bien el comportamiento de un circuito secuencial se puede describir convenientemente mediante un diagrama de estados, para su implementación se debe traducir la información contenida en el diagrama de estados a una tabla de estados. La forma tabular del diagrama de estado es la tabla de estado. El estado actual, el siguiente estado y la salida son las tres secciones del diagrama.
La tabla de estados del flip-flop JK es:
| Entradas | Estado actual | Producción | |
|---|---|---|---|
| j | k | q |
Q+ (Producción) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Ecuación de estado: Q n+1 = Q n bar J + Q n K bar
Reducción estatal:
La técnica de reducción de estado generalmente evita la adición de estados duplicados. La reducción de estados redundantes reduce el número de flip-flops y puertas lógicas, lo que reduce el costo del circuito final. Se dice que dos estados son equivalentes si cada posible conjunto de entradas genera exactamente la misma salida y el mismo estado siguiente. Cuando dos estados son iguales, uno de ellos puede eliminarse sin cambiar la relación entrada-salida. El algoritmo de reducción de estado se aplica en la tabla de estado para reducir estados equivalentes.
Asignación estatal:
La asignación de estados se refiere al proceso de asignar valores binarios a los estados de una máquina secuencial. Los valores binarios se deben dar a los estados de tal manera que las funciones de entrada de flip-flop se puedan implementar con un número mínimo de puertas lógicas.
Las reglas de asignación de estado son las siguientes:
Regla 1: los estados que tienen el mismo estado siguiente para una condición de entrada determinada deben tener asignaciones que se puedan agrupar en celdas lógicamente adyacentes en un K-map.
Regla 2: los estados que son los próximos estados de un solo estado deben tener asignaciones que se puedan agrupar en celdas lógicamente adyacentes en un K-map.
Ejemplo 1: Para explicar el concepto de reducción de estado, consideremos la tabla de estado como
| Estado actual | siguiente estado | Producción | ||
|---|---|---|---|---|
| X=0 | X=1 | X=0 | X=1 | |
| a | a | b | 0 | 0 |
| b | C | d | 0 | 0 |
| C | a | d | 0 | 0 |
| d | mi | F | 0 | 1 |
| mi | a | F | 0 | 1 |
| F | gramo | F | 0 | 1 |
| gramo | a | F | 0 | 1 |
El diagrama de estado para la tabla de estado anterior es
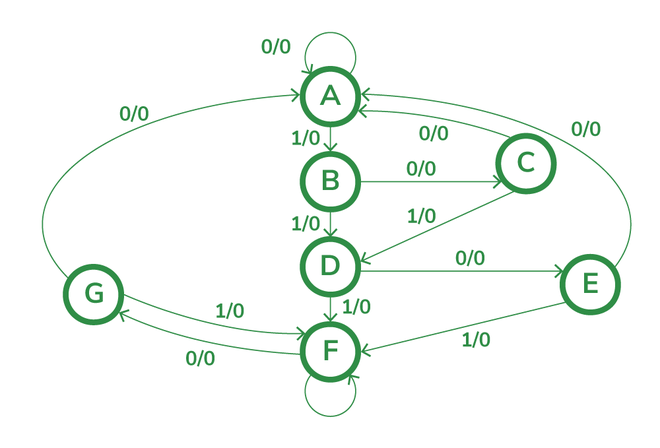
Diagrama de estado antes de la reducción
Paso 1: Primero aquí se supone que debemos identificar dos o más estados similares en el siguiente estado y estado de salida. En la tabla anterior, si observamos que los estados de e y g tienen el mismo estado siguiente y valores de salida para todas las combinaciones de entrada, es decir, X=0 y X=1.
Así que elimine el estado g en la tabla de estados y donde sea que esté presente reemplácelo con e. Porque e y g son lo mismo, es decir, e=g.
| Estado actual | siguiente estado | Producción | ||
|---|---|---|---|---|
| X=0 | X=1 | X=0 | X=1 | |
| a | a | b | 0 | 0 |
| b | C | d | 0 | 0 |
| C | a | d | 0 | 0 |
| d | mi | F | 0 | 1 |
| mi | a | F | 0 | 1 |
| F | e(g=e) | F | 0 | 1 |
Paso 2: Verifique nuevamente si dos estados tienen valores similares o no. Si dos estados tienen el mismo siguiente estado y salida, elimine un estado.
Aquí d y f tienen el mismo valor y salida del siguiente estado. Así que elimine f y donde sea que f esté presente, reemplácela con d. Porque los dos son iguales d=f
| Estado actual | siguiente estado | Producción | ||
|---|---|---|---|---|
| X=0 | X=1 | X=0 | X=1 | |
| a | a | b | 0 | 0 |
| b | C | d | 0 | 0 |
| C | a | d | 0 | 0 |
| d | mi | d(d=f) | 0 | 1 |
| mi | a | d(d=f) | 0 | 1 |
Paso 3: Observe más a fondo si hay estados similares presentes o no. Los estados c y e tienen los mismos estados siguientes pero tienen salidas diferentes. Por lo que no podemos considerarlo un estado de reducción.
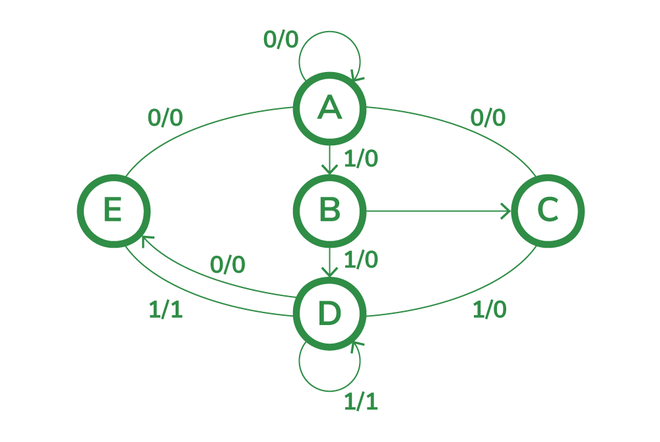
Diagrama de estado Después de la reducción
Paso 4: Si observaste la tabla de estados, los estados se representan usando el alfabeto. No podemos continuar si tenemos alfabetos, por lo que asignar números binarios a los alfabetos se denomina asignación de estado.
Para asignar números binarios al estado tenemos que considerar el número mínimo de bits.
Los códigos deben contener n bits para un circuito con m estados, donde 2 n >= m. En este caso, cada estado requiere 2 3 >=5=>3 bits para ser representado. Con tres bits, hay ocho combinaciones posibles, de las cuales cinco pueden usarse para representar los estados.
| Estado | Tarea 1 |
|---|---|
| Binario | |
| a | 000 |
| b | 001 |
| C | 010 |
| d | 011 |
| mi | 100 |
Paso 5: Reemplazar los alfabetos con números binarios.
| Estado actual | siguiente estado | Producción | ||
|---|---|---|---|---|
| X=0 | X=1 | X=0 | X=1 | |
| 000 | 000 | 001 | 0 | 0 |
| 001 | 010 | 011 | 0 | 0 |
| 010 | 000 | 011 | 0 | 0 |
| 011 | 100 | 011 | 0 | 1 |
| 100 | 000 | 011 | 0 | 1 |
Publicación traducida automáticamente
Artículo escrito por laxmigangarajula03 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA