Encuentre todos los elementos adyacentes de un elemento dado en una array o array 2D

Dada una array de enteros bidimensional arr[ ][ ] , devuelve todos los elementos adyacentes de un entero particular cuya posición se da como (x, y) .

Los elementos adyacentes son todos los elementos que comparten un lado o punto común, es decir, tienen una distancia vertical, horizontal o diagonal de 1.

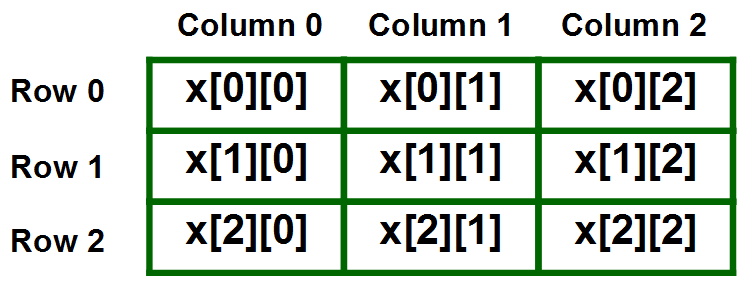
Un ejemplo de una array 2D

Ejemplos:

Entrada: arr[][] = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} }, x = 1, y = 1
Salida: {1, 2, 3, 4, 6, 7, 8, 9}
Explicación: Los elementos adyacentes a arr[1][1] (es decir, 5) son: 
arr[0][0], arr[0][1], arr[0][ 2], arr[1][0], arr[1][2], arr[2][0], arr[2][1] y arr[2][2].

Entrada: arr[][] = { {1, 2, 3}, {4, 5, 6}, {7, 8, 9} }, x = 0, y = 2
Salida: {2, 5, 6}

Método 1: en este enfoque, debemos verificar todas las posiciones adyacentes posibles e imprimirlas como los elementos adyacentes de los elementos dados.
El único problema de este enfoque es que una posible posición adyacente puede no ser una posición válida de la array, es decir, el índice puede estar fuera de los límites de la array bidimensional. Así que tenemos que seguir comprobando cada posición adyacente si esa es una posición válida o no.

A continuación se muestra la implementación del enfoque anterior.

// C++ code to implement the approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to check whether
// position is valid or not
bool isValidPos(int i, int j, int n, int m)
{
    if (i < 0 || j < 0 || i > n - 1 || j > m - 1)
        return 0;
    return 1;
}
 
// Function that returns all ajdacent elements
vector<int> getAdjacent(vector<vector<int> >& arr, int i,
                        int j)
{
    // Size of given 2d array
    int n = arr.size();
    int m = arr[0].size();
 
    // Initialising a vector array
    // where ajdacent element will be stored
    vector<int> v;
 
    // Checking for all the possible adjacent positions
    if (isValidPos(i - 1, j - 1, n, m))
        v.push_back(arr[i - 1][j - 1]);
    if (isValidPos(i - 1, j, n, m))
        v.push_back(arr[i - 1][j]);
    if (isValidPos(i - 1, j + 1, n, m))
        v.push_back(arr[i - 1][j + 1]);
    if (isValidPos(i, j - 1, n, m))
        v.push_back(arr[i][j - 1]);
    if (isValidPos(i, j + 1, n, m))
        v.push_back(arr[i][j + 1]);
    if (isValidPos(i + 1, j - 1, n, m))
        v.push_back(arr[i + 1][j - 1]);
    if (isValidPos(i + 1, j, n, m))
        v.push_back(arr[i + 1][j]);
    if (isValidPos(i + 1, j + 1, n, m))
        v.push_back(arr[i + 1][j + 1]);
 
    // Returning the vector
    return v;
}
 
// Driver Code
int main()
{
    // Given vector array
    vector<vector<int> > arr{ { 1, 2, 3 },
                              { 4, 5, 6 },
                              { 7, 8, 9 } };
    int x = 1, y = 1;
 
    // Function call
    vector<int> ans = getAdjacent(arr, x, y);
 
    // Print all the adjacent elements
    for (int i = 0; i < ans.size(); i++) {
        cout << ans[i] << " ";
    }
    return 0;
}

// Java code to implement the approach
 
import java.io.*;
import java.util.*;
 
class GFG {
 
    // Function to check whether position is valid or not
    static boolean isValidPos(int i, int j, int n, int m)
    {
        if (i < 0 || j < 0 || i > n - 1 || j > m - 1) {
            return false;
        }
        return true;
    }
 
    // Function that returns all ajdacent elements
    static List<Integer>
    getAdjacent(List<List<Integer> > arr, int i, int j)
    {
        // Size of given 2d array
        int n = arr.size();
        int m = arr.get(0).size();
 
        // Initialising a array list where ajdacent element
        // will be stored
        List<Integer> v = new ArrayList<>();
 
        // Checking for all the possible adjacent positions
        if (isValidPos(i - 1, j - 1, n, m)) {
            v.add(arr.get(i - 1).get(j - 1));
        }
        if (isValidPos(i - 1, j, n, m)) {
            v.add(arr.get(i - 1).get(j));
        }
        if (isValidPos(i - 1, j + 1, n, m)) {
            v.add(arr.get(i - 1).get(j + 1));
        }
        if (isValidPos(i, j - 1, n, m)) {
            v.add(arr.get(i).get(j - 1));
        }
        if (isValidPos(i, j + 1, n, m)) {
            v.add(arr.get(i).get(j + 1));
        }
        if (isValidPos(i + 1, j - 1, n, m)) {
            v.add(arr.get(i + 1).get(j - 1));
        }
        if (isValidPos(i + 1, j, n, m)) {
            v.add(arr.get(i + 1).get(j));
        }
        if (isValidPos(i + 1, j + 1, n, m)) {
            v.add(arr.get(i + 1).get(j + 1));
        }
 
        // Returning the arraylist
        return v;
    }
 
    public static void main(String[] args)
    {
 
        List<List<Integer> > arr = new ArrayList<>();
 
        arr.add(
            new ArrayList<Integer>(Arrays.asList(1, 2, 3)));
        arr.add(
            new ArrayList<Integer>(Arrays.asList(4, 5, 6)));
        arr.add(
            new ArrayList<Integer>(Arrays.asList(7, 8, 9)));
 
        int x = 1, y = 1;
 
        // Function call
        List<Integer> ans = getAdjacent(arr, x, y);
 
        // Print all the adjacent elements
        for (int i = 0; i < ans.size(); i++) {
            System.out.print(ans.get(i) + " ");
        }
    }
}
 
// This code is contributed by lokeshmvs21.

# python code to implement the approach
 
# Function to check whether
# position is valid or not
 
 
def isValidPos(i, j, n, m):
 
    if (i < 0 or j < 0 or i > n - 1 or j > m - 1):
        return 0
    return 1
 
 
# Function that returns all ajdacent elements
def getAdjacent(arr, i, j):
 
    # Size of given 2d array
    n = len(arr)
    m = len(arr[0])
 
    # Initialising a vector array
    # where ajdacent element will be stored
    v = []
 
    # Checking for all the possible adjacent positions
    if (isValidPos(i - 1, j - 1, n, m)):
        v.append(arr[i - 1][j - 1])
    if (isValidPos(i - 1, j, n, m)):
        v.append(arr[i - 1][j])
    if (isValidPos(i - 1, j + 1, n, m)):
        v.append(arr[i - 1][j + 1])
    if (isValidPos(i, j - 1, n, m)):
        v.append(arr[i][j - 1])
    if (isValidPos(i, j + 1, n, m)):
        v.append(arr[i][j + 1])
    if (isValidPos(i + 1, j - 1, n, m)):
        v.append(arr[i + 1][j - 1])
    if (isValidPos(i + 1, j, n, m)):
        v.append(arr[i + 1][j])
    if (isValidPos(i + 1, j + 1, n, m)):
        v.append(arr[i + 1][j + 1])
 
    # Returning the vector
    return v
 
 
# Driver Code
if __name__ == "__main__":
 
    # Given vector array
    arr = [[1, 2, 3],
           [4, 5, 6],
           [7, 8, 9]]
    x, y = 1, 1
 
    # Function call
    ans = getAdjacent(arr, x, y)
 
    # Print all the adjacent elements
    for i in range(0, len(ans)):
        print(ans[i], end=" ")
 
    # This code is contributed by rakeshsahni

using System;
using System.Collections.Generic;
 
public class GFG{
 
  // Function to check whether
  // position is valid or not
  public static bool isValidPos(int i, int j, int n, int m)
  {
    if (i < 0 || j < 0 || i > n - 1 || j > m - 1)
      return false;
    return true;
  }
 
  // Function that returns all ajdacent elements
  public static List<int> getAdjacent(int[][] arr, int i,
                                      int j)
  {
    // Size of given 2d array
    int n = arr.Length;
    int m = arr[0].Length;
 
    // Initialising a list
    // where ajdacent element will be stored
 
    List<int> v = new List<int>();
 
    // Checking for all the possible adjacent positions
    if (isValidPos(i - 1, j - 1, n, m))
    { v.Add(arr[i - 1][j - 1]);}
    if (isValidPos(i - 1, j, n, m))
    {  v.Add(arr[i - 1][j]);}
    if (isValidPos(i - 1, j + 1, n, m))
    { v.Add(arr[i - 1][j + 1]);}
    if (isValidPos(i, j - 1, n, m))
    {  v.Add(arr[i][j - 1]);}
    if (isValidPos(i, j + 1, n, m))
    { v.Add(arr[i][j + 1]);}
    if (isValidPos(i + 1, j - 1, n, m))
    { v.Add(arr[i + 1][j - 1]);}
    if (isValidPos(i + 1, j, n, m))
    { v.Add(arr[i + 1][j]);}
    if (isValidPos(i + 1, j + 1, n, m))
    {  v.Add(arr[i + 1][j + 1]);}
 
    // Returning the list
    return v;
  }
 
  static public void Main (){
 
    // Given array
    int[][] arr = new int[3][]{ new int[]{ 1, 2, 3 },
                               new int[] { 4, 5, 6 },
                               new int[] { 7, 8, 9 } };
 
 
    int x = 1, y = 1;
 
    // Function call
    List<int> ans = getAdjacent(arr, x, y);
 
    // Print all the adjacent elements
    for (int i = 0; i < ans.Count; i++) {
      System.Console.Write(ans[i]);
      System.Console.Write(" ");
    }
 
  }
}
 
// This code is contributed by akashish__

<script>
       // JavaScript code for the above approach
 
       // Function to check whether
       // position is valid or not
       function isValidPos(i, j, n, m) {
           if (i < 0 || j < 0 || i > n - 1 || j > m - 1)
               return 0;
           return 1;
       }
 
       // Function that returns all ajdacent elements
       function getAdjacent(arr, i, j) {
           // Size of given 2d array
           let n = arr.length;
           let m = arr[0].length;
 
           // Initialising a vector array
           // where ajdacent element will be stored
           let v = [];
 
           // Checking for all the possible adjacent positions
           if (isValidPos(i - 1, j - 1, n, m))
               v.push(arr[i - 1][j - 1]);
           if (isValidPos(i - 1, j, n, m))
               v.push(arr[i - 1][j]);
           if (isValidPos(i - 1, j + 1, n, m))
               v.push(arr[i - 1][j + 1]);
           if (isValidPos(i, j - 1, n, m))
               v.push(arr[i][j - 1]);
           if (isValidPos(i, j + 1, n, m))
               v.push(arr[i][j + 1]);
           if (isValidPos(i + 1, j - 1, n, m))
               v.push(arr[i + 1][j - 1]);
           if (isValidPos(i + 1, j, n, m))
               v.push(arr[i + 1][j]);
           if (isValidPos(i + 1, j + 1, n, m))
               v.push(arr[i + 1][j + 1]);
 
           // Returning the vector
           return v;
       }
 
       // Driver Code
 
       // Given vector array
       let arr = [[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]];
       let x = 1, y = 1;
 
       // Function call
       let ans = getAdjacent(arr, x, y);
 
       // Print all the adjacent elements
       for (let i = 0; i < ans.length; i++) {
           document.write(ans[i] + " ");
       }
        
   // This code is contributed by Potta Lokesh
   </script>

1 2 3 4 6 7 8 9 

Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)

Método 2: en este enfoque, no verificaremos para cada elemento adyacente si es una posición válida o no, codificaremos directamente de manera que solo imprima los elementos válidos.

• Vamos a iterar usando dos bucles, donde el bucle exterior indica la desviación en el número de fila y el bucle interior indica la desviación en el número de columna. La desviación está en el rango de -1 a 1 y se ajusta según la posición proporcionada.
• Aquí hay solo un caso especial: si ambas desviaciones son 0, entonces denota el mismo elemento.

A continuación se muestra la implementación del enfoque anterior.

// C++ code to implement the approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function that returns all the ajdacent elements
vector<int> getAdjacent(vector<vector<int> >& arr, int i,
                        int j)
{
    // Size of given 2d array
    int n = arr.size();
    int m = arr[0].size();
 
    // Initialising a vector array where
    // ajdacent elements will be stored
    vector<int> v;
 
    // Checking for adjacent elements
    // and adding them to array
 
    // Deviation of row that gets adjusted
    // according to the provided position
    for (int dx = (i > 0 ? -1 : 0); dx <= (i < n ? 1 : 0);
         ++dx) {
 
        // Deviation of the column that
        // gets adjusted according to
        // the provided position
        for (int dy = (j > 0 ? -1 : 0);
             dy <= (j < m ? 1 : 0); ++dy) {
            if (dx != 0 || dy != 0) {
                v.push_back(arr[i + dx][j + dy]);
            }
        }
    }
 
    // Returning the vector array
    return v;
}
 
// Driver Code
int main()
{
    // Given vector array
    vector<vector<int> > arr{ { 1, 2, 3 },
                              { 4, 5, 6 },
                              { 7, 8, 9 } };
    int x = 1, y = 1;
 
    // Function call
    vector<int> ans = getAdjacent(arr, x, y);
 
    // Print all the adjacent elements
    for (int i = 0; i < ans.size(); i++) {
        cout << ans[i] << " ";
    }
    return 0;
}

using System;
using System.Collections.Generic;
 
public class GFG{
 
  // Function that returns all the ajdacent elements
  public static List<int> getAdjacent(int[][] arr, int i,
                                      int j)
  {
    // Size of given 2d array
    int n = arr.Length;
    int m = arr[0].Length;
 
    // Initialising a vector array where
    // ajdacent elements will be stored
    List<int> v = new List<int>();
 
    // Checking for adjacent elements
    // and adding them to array
 
    // Deviation of row that gets adjusted
    // according to the provided position
    for (int dx = (i > 0 ? -1 : 0); dx <= (i < n ? 1 : 0);
         ++dx) {
 
      // Deviation of the column that
      // gets adjusted according to
      // the provided position
      for (int dy = (j > 0 ? -1 : 0);
           dy <= (j < m ? 1 : 0); ++dy) {
        if (dx != 0 || dy != 0) {
          v.Add(arr[i + dx][j + dy]);
        }
      }
    }
 
    // Returning the vector array
    return v;
  }
 
 
  static public void Main (){
 
    // Given vector array
    int[][] arr = new int[3][]{new int[] { 1, 2, 3 },
                               new int[] { 4, 5, 6 },
                               new int[] { 7, 8, 9 } };
    int x = 1, y = 1;
 
    // Function call
    List<int> ans = getAdjacent(arr, x, y);
 
    // Print all the adjacent elements
    for (int i = 0; i < ans.Count; i++) {
      System.Console.Write(ans[i]);
      System.Console.Write(" ");
 
    }
  }
}
 
// This code is contributed by akashish__

// JavaScript code to implement the approach
 
// Function that returns all the ajdacent elements
function getAdjacent(arr, i, j)
{
 
    // Size of given 2d array
    let n = arr.length;
    let m = arr[0].length;
 
    // Initialising a vector array where
    // ajdacent elements will be stored
    let v = [];
 
    // Checking for adjacent elements
    // and adding them to array
 
    // Deviation of row that gets adjusted
    // according to the provided position
    for (var dx = (i > 0 ? -1 : 0); dx <= (i < n ? 1 : 0);
         ++dx) {
 
        // Deviation of the column that
        // gets adjusted according to
        // the provided position
        for (var dy = (j > 0 ? -1 : 0);
             dy <= (j < m ? 1 : 0); ++dy) {
            if (dx != 0 || dy != 0) {
                v.push(arr[i + dx][j + dy]);
            }
        }
    }
 
    // Returning the vector array
    return v;
}
 
// Driver Code
 
// Given vector array
let arr = [ [1, 2, 3 ], [ 4, 5, 6 ], [7, 8, 9 ]];
let x = 1, y = 1;
 
// Function call
let ans = getAdjacent(arr, x, y);
 
// Print all the adjacent elements
for (var i = 0; i < ans.length; i++)
    process.stdout.write(ans[i] + " ");
 
// This code is contributed by phasing17

1 2 3 4 6 7 8 9 

Complejidad temporal: O(1) 
Espacio auxiliar: O(1)