Prueba de dos colas de proporción poblacional en R

Una prueba de hipótesis estadística consiste en poner a prueba su suposición sobre los parámetros de la población y verificar si su suposición sigue siendo válida calculando y comparando los parámetros de la población con las estadísticas de prueba.

Los pasos convencionales que se siguen al formular la prueba de hipótesis, se enumeran a continuación

• Enunciar hipótesis nula (Ho) e hipótesis alternativa (Ha)
• Recopile una muestra relevante de datos para probar la hipótesis.
• Elija un nivel de significación para la prueba de hipótesis.
• Realice una prueba estadística adecuada.
• Con base en las estadísticas de prueba y el valor p, decida si rechazar o no rechazar su hipótesis nula.

En general, la prueba de hipótesis se realiza para estimar la media de la población y la proporción de la población. En este artículo, analicemos cómo realizar una prueba de proporción de la población de dos colas. Una prueba de dos colas en general es un método en el que el área crítica de una distribución es de dos lados (ambos extremos) y prueba si una muestra es mayor o menor que un rango específico de valores.

Prueba de dos colas con alfa = 0.05, (0.025 en cualquier lado) 

La prueba de hipótesis para proporciones implica medir dos resultados, como el éxito o el fracaso, verdadero o falso, bueno o malo, y así sucesivamente en un conjunto definido de ensayos. La probabilidad de éxito o fracaso debe ser la misma durante todo el ensayo.  

Tomemos un ejemplo más realista, hoy en día el cibercrimen es una gran amenaza en línea, así que consideremos un caso de transacción fraudulenta con tarjeta de crédito. Supongamos que una firma bancaria popular realizó un estudio durante varios años y obtuvo valores de referencia estándar de la probabilidad de que cualquier transacción sea fraudulenta es del 5%, lo que a la inversa significa que la probabilidad de que cualquier transacción no sea fraudulenta es del 9%. Así que aquí la probabilidad de éxito es 0,95 y la de fracaso es 0,05 y supongamos que estos números van a ser constantes para cualquier transacción con tarjeta de crédito. 

Un buen día, una empresa bancaria competitiva desea desafiar estos números y desea realizar una prueba de hipótesis para demostrar que la probabilidad de una transacción fraudulenta no es igual al 2%. La firma bancaria competitiva toma muestras de 25 transacciones aleatorias y encontró que 2 de 25 transacciones fueron fraudulentas. . Formulemos la hipótesis de la proporción de la población basada en el problema anterior.

Hipótesis Nula: La probabilidad de que cualquier transacción sea fraudulenta es del 5% p = po (Aquí, po = 0.05) 

Hipótesis Alterna: La probabilidad de que cualquier transacción sea fraudulenta no es igual al 5%   p != po

alfa: 0.05

Definamos el estadístico de prueba de la siguiente manera

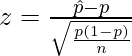
dónde,

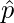•  : proporción de la muestra
• p = proporción de la población
• n = tamaño de la muestra

Ejemplo:

Calculemos la función estadística de prueba usando R como se muestra a continuación

pbar = 2/25 # sample proportion 
p0 = 0.05 # hypothesized value 
n = 25 # sample size 
z = (pbar-p0)/sqrt(p0*(1-p0)/n) # test statistic
z

Producción:

z = 0.688247201611683

Ahora calculemos los valores críticos a un nivel de significancia de 0.05.

alpha = .05 
z.half.alpha = qnorm(1-alpha/2) 
c(-z.half.alpha, z.half.alpha) 

Producción:

-1.95996398454005,  1.95996398454005

La estadística de prueba calculada 0,68824720 se encuentra entre los valores críticos -1,9600 y 1,9600. Por lo tanto, en el nivel de significancia de .05, no podemos rechazar la hipótesis nula . En otras palabras, no tenemos suficiente evidencia para concluir que la probabilidad de una transacción fraudulenta no es igual al 5%.