En física, la frecuencia y la longitud de onda son características importantes relacionadas con un ciclo de onda. Ahora, ¿qué es una onda? La transferencia de energía de un punto a otro por una perturbación o variación se conoce como onda. Ahora bien, la longitud de onda se define como la distancia entre dos puntos sucesivos en fase entre sí, mientras que la frecuencia se define como el número de ondas producidas por segundo.
Frecuencia
El número total de ciclos de onda u oscilaciones producidas por unidad de tiempo se denomina frecuencia (f) de una onda. Se mide en términos de Hertz (Hz) o s -1 . Para los humanos, el rango audible de frecuencias de sonido es de 20 Hz a 20 kHz. Los oídos humanos no pueden oír los sonidos ultrasónicos, es decir, las frecuencias por encima del rango audible, ni tampoco los infrasonidos, es decir, las frecuencias por debajo del rango audible.
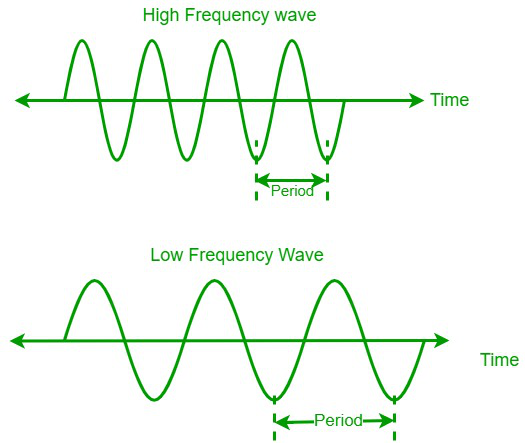
La fórmula para la frecuencia de una onda es,
Frecuencia (f) = 1/T
Donde T es el periodo de una onda.
- El período de una onda se define como el tiempo que tarda una onda en completar un ciclo completo o completar una oscilación.
- De la fórmula de la frecuencia, podemos observar que la frecuencia de una onda es inversamente proporcional a su período.
1 Hercio = 1 oscilación/segundo
Longitud de onda
La longitud de la distancia entre las dos crestas o valles sucesivos de una onda se denomina longitud de onda. La cresta es el punto más alto de la ola, mientras que el punto más bajo de la ola es el valle. Como la longitud de onda es una distancia o longitud entre dos puntos, se mide en metros, centímetros, milímetros, micrómetros, Angstroms, etc. Se denota con el símbolo griego Lambda ‘λ’.

La fórmula para la longitud de onda es,
Longitud de onda (λ) = velocidad (v)/frecuencia (f)
⇒ λ = v/f
- La distancia recorrida por la onda en una unidad de tiempo se llama velocidad de una onda o velocidad de onda. La unidad SI de velocidad de onda es ms -1 .
- La velocidad de una onda es igual al producto de su longitud de onda y su frecuencia.
v = λ × f
La distancia recorrida por una onda en una unidad de tiempo es igual a una longitud de onda.
⇒ Velocidad de onda (v) = Longitud de onda (λ)/Período (T)
Lo sabemos,
frecuencia (f) = 1/Periodo(T)
⇒ Velocidad de onda (v) = Longitud de onda (λ) × Frecuencia (f)
⇒ v = λ × f
⇒ λ = v/f
¿Cómo cambia la longitud de onda de una onda cuando la frecuencia disminuye cuando la frecuencia aumenta?
Responder:
Consideremos un hilo que está atado a un extremo. Ahora sostenga el otro extremo de la cuerda y oscílelo más rápido, lo que resultará en ondas de mayor frecuencia. También podemos observar que las ondas se producen con una longitud de onda más corta. Por lo tanto, podemos sacar la conclusión de que existe una relación entre la longitud de onda y la frecuencia.
A partir de la ecuación de la longitud de onda, podemos decir que la longitud de onda de una onda es inversamente proporcional a su frecuencia, es decir, a medida que aumenta la frecuencia de una onda, su longitud de onda disminuye. De manera similar, a medida que la frecuencia de una onda disminuye, su longitud de onda aumenta.
λ ∝ 1/f
Por ejemplo, consideremos una onda cuya nueva frecuencia es el doble de su frecuencia anterior. Ahora bien, ¿cuál será la nueva longitud de onda de la onda?
Dados los datos,
Sean λ y λ’ las longitudes de onda vieja y nueva de la onda de luz.
Sea f la frecuencia antigua de la onda.
Ahora, la nueva frecuencia de la onda = 2f
Longitud de onda (λ) = Velocidad/Frecuencia
La velocidad de la onda permanece constante.
⇒ λ ∝ 1/f
⇒ λ 1 / λ 2 = f 2 / f 1
⇒ λ/λ’ = (2f)/f = 2
⇒ λ’ = λ/2
Por lo tanto, la nueva longitud de onda de la onda es la mitad de la longitud de onda anterior.
Por lo tanto, a medida que aumenta la frecuencia de una onda, disminuye su longitud de onda.
Por lo tanto, a medida que disminuye la frecuencia de una onda, aumenta su longitud de onda.
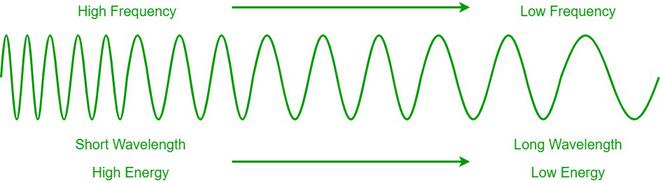
- Una onda con una frecuencia alta tiene una longitud de onda corta y una energía alta.
- Una onda con una frecuencia baja tiene una longitud de onda larga y una energía baja.
Problemas de muestra
Problema 1: Dos ondas sonoras viajan por el aire a la misma velocidad. Si una onda cuya frecuencia es de 45 kHz tiene una longitud de onda de 7,5 mm, encuentre la frecuencia de la onda cuya longitud de onda es de 100 nm.
Solución:
Dados los datos,
La velocidad de ambas ondas es igual ⇒ v 1 = v 2 = v, donde v es la velocidad de una onda de sonido
La longitud de onda de la primera onda ( λ 1 ) =7,5 mm = 7,5 × 10 -3 m
Frecuencia de la primera onda (f 1 ) = 45 kHz = 45 × 10 3 Hz
Longitud de onda de la segunda onda (λ 2 ) = 100 nm = 100 × 10 -9 m
Frecuencia de la segunda onda (f 2 ) =?
Longitud de onda (λ) = Velocidad/Frecuencia
⇒ λ ∝ 1/f
⇒ λ 1 / λ 2 = f 2 / f 1
⇒ (7,5 × 10 -3 )/(100 × 10 -9 ) = f 2 /(45 × 10 3 )
⇒ f 2 = [(7.5 × 10 -3 ) × (45 × 10 3 )]/(100 × 10 -9 )
⇒ f2 = 33,75 GHz
Por lo tanto, la frecuencia de la longitud de onda de 100 nm es 33,75 GHz.
Por lo tanto, a medida que disminuye la longitud de onda de una onda, aumenta su frecuencia.
Problema 2: Una onda de luz viaja en el vacío. ¿Cuál será la nueva longitud de onda de la onda si la nueva frecuencia de la onda es una quinta parte de su frecuencia anterior?
Solución:
Dados los datos,
Sean λ y λ’ las longitudes de onda vieja y nueva de la onda de luz.
Sea f la frecuencia antigua de la onda.
Ahora, la nueva frecuencia de la onda = f/5
Longitud de onda (λ) = Velocidad/Frecuencia
La velocidad de la onda permanece constante.
⇒ λ ∝ 1/f
⇒ λ 1 / λ 2 = f 2 / f 1
⇒ λ/λ’ = (f/5)/f = 1/5
⇒ λ’ = 5λ
Por lo tanto, la nueva longitud de onda de la onda es cinco veces la longitud de onda anterior.
Por lo tanto, a medida que disminuye la frecuencia de una onda, aumenta su longitud de onda.
Problema 3: Dos ondas de sonido que viajan a través del agua a la misma velocidad. Si una onda cuya frecuencia es de 3 MHz tiene una longitud de onda de 100 m, encuentre la longitud de onda de la onda cuya frecuencia es de 4,5 kHz.
Solución:
Dados los datos,
La longitud de onda de la primera onda ( λ 1 ) = 100 m
Frecuencia de la primera onda (f 1 ) = 3 MHz = 3 × 10 6 Hz
Frecuencia de la segunda onda (f 2 ) = 4,5 kHz = 4,5 × 10 3 Hz
La longitud de onda de la segunda onda ( λ 2 ) = ?
La velocidad de ambas ondas es igual ⇒ v 1 = v 2 = v
Longitud de onda (λ) = Velocidad/Frecuencia
⇒ λ ∝ 1/f
⇒ λ 1 / λ 2 = f 2 / f 1
⇒ 100/ λ 2 = (4,5 × 10 3 )/(3 × 10 6 )
⇒ λ 2 = (3 × 10 6 × 100 )/(4,5 × 10 3 ) = 66,67 km
Por lo tanto, la onda de frecuencia de 4,5 kHz de longitud de onda es de 66,67 km.
Por lo tanto, a medida que disminuye la frecuencia de una onda, aumenta su longitud de onda.
Problema 4: Una onda de luz viaja en el vacío. ¿Cuál será la nueva longitud de onda de la onda si la nueva frecuencia de la onda es tres veces su frecuencia anterior?
Solución:
Dados los datos,
Sean λ y λ’ las longitudes de onda vieja y nueva de la onda de luz.
Sea f la frecuencia antigua de la onda.
Ahora, la nueva frecuencia de la onda = 3f
Longitud de onda (λ) = Velocidad/Frecuencia
La velocidad de la onda permanece constante.
⇒ λ ∝ 1/f
⇒ λ 1 / λ 2 = f 2 / f 1
⇒ λ/λ’ = 3f/f = 3
⇒ λ’ = λ/3
Por lo tanto, la nueva longitud de onda de la onda es un tercio de la longitud de onda anterior.
Por lo tanto, a medida que aumenta la frecuencia de una onda, disminuye su longitud de onda.
Problema 5: Una onda de luz viaja en el vacío. ¿Cuál será la nueva frecuencia de la onda si la nueva longitud de onda de la onda es cuatro veces su longitud de onda anterior?
Solución:
Dados los datos,
Sean f y F las frecuencias antigua y nueva de la onda de luz.
Sea λ la antigua longitud de onda de la onda.
Ahora, la nueva longitud de onda de la onda = 4λ
Longitud de onda (λ) = Velocidad/Frecuencia
La velocidad de la onda permanece constante.
⇒ λ ∝ 1/f
⇒ λ 1 / λ 2 = f 2 / f 1
⇒ λ /4λ = F/f
⇒ F/f = 1/4 ⇒ F = f/4
Por lo tanto, la nueva frecuencia de la onda es un cuarto de la frecuencia anterior.
Por lo tanto, a medida que aumenta la longitud de onda de una onda, disminuye su frecuencia.
Problema 6: dos notas sonoras producidas por un diapasón viajan a la misma velocidad. Si una onda cuya frecuencia es de 6 kHz tiene una longitud de onda de 100 mm, encuentre la longitud de onda de la onda cuya frecuencia es de 5,4 kHz.
Dados los datos,
La longitud de onda de la primera onda ( λ 1 ) = 100 × 10 -3 m = 0,1 m
Frecuencia de la primera onda (f 1 ) = 6 kHz = 6 × 10 3 Hz
Frecuencia de la segunda onda (f 2 ) = 5,4 kHz = 5,4 × 10 3 Hz
La longitud de onda de la segunda onda ( λ 2 ) =?
La velocidad de ambas ondas es igual ⇒ v 1 = v 2 = v
Longitud de onda (λ) = Velocidad/Frecuencia
⇒ λ ∝ 1/f
⇒ λ 1 / λ 2 = f 2 / f 1
⇒ (0.1)/ λ 2 = (5.4 × 10 3 )/(6 × 10 3 )
⇒ λ 2 = (6 × 10 3 × 0,1 )/(5,4 × 10 3 ) = 0,111 m = 111 mm
Por lo tanto, la onda de frecuencia de 4,5 kHz de longitud de onda es de 111 mm.
Por lo tanto, a medida que disminuye la frecuencia de una onda, aumenta su longitud de onda.
Problema 7: Si la nueva frecuencia de una onda electromagnética es dos tercios de su frecuencia anterior, ¿cuál será la nueva longitud de onda de la onda?
Solución:
Dados los datos,
Sean λ y λ’ las longitudes de onda vieja y nueva de la onda de luz.
Sea f la frecuencia antigua de la onda.
Ahora, la nueva frecuencia de la onda = (2/3)f
Longitud de onda (λ) = Velocidad/Frecuencia
La velocidad de la onda permanece constante.
⇒ λ ∝ 1/f
⇒ λ 1 / λ 2 = f 2 / f 1
⇒ λ/λ’ = (2/3)f/f = 2/3
⇒ λ’ = 3λ/2 = 1,5λ
Por tanto, la nueva longitud de onda de la onda es tres veces y media su antigua longitud de onda.
Publicación traducida automáticamente
Artículo escrito por kiran086472 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA