Implementación de la pila utilizando la lista doblemente enlazada

Las listas apiladas y doblemente enlazadas son dos estructuras de datos importantes con sus propios beneficios. Stack es una estructura de datos que sigue la técnica LIFO y se puede implementar utilizando arrays o estructuras de datos de lista enlazada. La lista doblemente enlazada tiene la ventaja de que también puede atravesar el Node anterior con la ayuda del puntero «anterior».

Lista doblemente enlazada:

• La lista doblemente enlazada (DLL) es una lista enlazada que contiene Nodes que se dividen en tres partes, es decir, datos, puntero siguiente y punteros anteriores.
• El puntero anterior apunta al Node anterior y el puntero siguiente apunta al Node próximo al Node actual.
• El puntero de inicio apunta al primer Node de la lista enlazada.

La estructura de una DLL se muestra a continuación.

// Declaration of Doubly Linked List
struct Node {
    int data;
    struct Node* next;
    struct Node* prev;
};

Pila: 

• Una pila es una estructura de datos lineal en la que se accede a los elementos a través de un puntero llamado «parte superior» de la pila.
• Sigue la técnica LIFO (Last In First Out).
• Se puede implementar por array o lista enlazada.

Funciones a implementar:

Algunas de las funcionalidades básicas en una pila cubiertas aquí son:

1. empujar()
2. estallido() 
3. esta vacio()
4. pila de impresión()
5. tamaño de la pila()
6. elemento superior()

1. empujar():

Si la pila está vacía, tome un nuevo Node, agréguele datos y asígnele «nulo» a su puntero anterior y siguiente, ya que es el primer Node de la DLL. Asigne arriba y comience como el nuevo Node. De lo contrario, tome un nuevo Node, agréguele datos y asigne el puntero «anterior» del nuevo Node al Node «superior» anterior y siguiente como «nulo». Además, actualice el puntero «superior» para contener el valor del nuevo Node, ya que ahora será el elemento superior de la pila.

Sintaxis:

empujar(d);

A continuación se muestra la implementación del método.

void push(int d)
{
    struct Node* n;
    n = new Node();
    n->data = d;
    if (isEmpty()) {
        n->prev = NULL;
        n->next = NULL;
 
        // As it is first node
        // if stack is empty
        start = n;
        top = n;
    }
    else {
        top->next = n;
        n->next = NULL;
        n->prev = top;
        top = n;
    }
}

Complejidad de tiempo: O(1)

2. pop(): 

Si la pila está vacía, imprima que la pila está vacía. De lo contrario, asigne superior -> anterior -> siguiente como «nulo» y asigne superior como superior-> anterior.

Sintaxis:

estallido();

A continuación se muestra la implementación del método.

void pop()
{
    struct Node* n;
    n = top;
    if (isEmpty())
        printf("Stack is empty");
    else if (top == start) {
        top = NULL;
        start = NULL;
        free(n);
    }
    else {
        top->prev->next = NULL;
        top = n->prev;
        free(n);
    }
}

Complejidad de tiempo: O(1)

3. estáVacío(): 

Compruebe el puntero superior. Si es «nulo» , devuelve verdadero . De lo contrario, devuelve falso .

Sintaxis:

esta vacio();

A continuación se muestra la implementación del método.

bool isEmpty()
{
    if (start == NULL)
        return true;
    return false;
}

Complejidad de tiempo: O(1)

4. pila de impresión(): 

Si la pila está vacía, imprima que la pila está vacía. De lo contrario, recorra la lista doblemente enlazada de principio a fin e imprima los datos de cada Node.

Sintaxis:

pila de impresión();

A continuación se muestra la implementación del método.

void printstack()
{
    if (isEmpty())
        printf("Stack is empty");
    else {
        struct Node* ptr = start;
        printf("Stack is :  ");
        while (ptr != NULL) {
            printf("%d   ", ptr->data);
            ptr = ptr->next;
        }
        printf("\n");
    }
}

Complejidad de tiempo: O(N) donde N es el tamaño de la pila

5. tamaño de pila(): 

Si la pila está vacía, devuelva cero; de lo contrario, itere de principio a fin y cuente el número de Nodes de la lista doblemente vinculada.

Sintaxis:

tamaño de la pila();

A continuación se muestra la implementación del método.

void stacksize()
{
    int c = 0;
    if (isEmpty())
        printf("Stack is empty");
    else {
        struct Node* ptr = start;
        while (ptr != NULL) {
            c++;
            ptr = ptr->next;
        }
    }
    printf(" Size of the stack is : %d \n ", c);
}

Complejidad de tiempo: O(N) donde N es el tamaño de la pila

6. elemento superior(): 

Si la pila está vacía, entonces no hay ningún elemento superior. De lo contrario, imprima el elemento en el Node superior de la pila.

Sintaxis:

elemento superior();

A continuación se muestra la implementación del método.

void topelement()
{
    if (isEmpty())
        printf("Stack is empty");
    else
        printf(
            "The element at top of the stack is : %d   \n",
            top->data);
}

Complejidad de tiempo: O(1)

Implementación de Stack usando listas doblemente enlazadas:

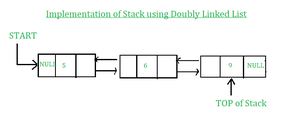
Implementación de Stack usando listas doblemente enlazadas:

A continuación se muestra la implementación de la pila utilizando una lista doblemente enlazada.

// A complete working program to
// demonstrate all stack operations using
// a doubly linked list
 
#include <iostream>
struct Node {
    int data;
    struct Node* prev;
    struct Node* next;
};
Node* start = NULL;
Node* top = NULL;
 
// Check if stack is empty
bool isEmpty()
{
    if (start == NULL)
        return true;
    return false;
}
 
// pushes element onto stack
void push(int d)
{
    struct Node* n;
    n = new Node();
    n->data = d;
    if (isEmpty()) {
        n->prev = NULL;
        n->next = NULL;
 
        // As it is first node if stack
        // is empty
        start = n;
        top = n;
    }
    else {
        top->next = n;
        n->next = NULL;
        n->prev = top;
        top = n;
    }
}
 
// Pops top element from stack
void pop()
{
    struct Node* n;
    n = top;
    if (isEmpty())
        printf("Stack is empty");
    else if (top == start) {
        top = NULL;
        start = NULL;
        free(n);
    }
    else {
        top->prev->next = NULL;
        top = n->prev;
        free(n);
    }
}
 
// Prints top element of the stack
void topelement()
{
    if (isEmpty())
        printf("Stack is empty");
    else
        printf(
            "The element at top of the stack is : %d   \n",
            top->data);
}
 
// Determines the size of the stack
void stacksize()
{
    int c = 0;
    if (isEmpty())
        printf("Stack is empty");
    else {
        struct Node* ptr = start;
        while (ptr != NULL) {
            c++;
            ptr = ptr->next;
        }
    }
    printf("Size of the stack is : %d \n ", c);
}
 
// Determines the size of the stack
void printstack()
{
    if (isEmpty())
        printf("Stack is empty");
    else {
        struct Node* ptr = start;
        printf("Stack is :  ");
        while (ptr != NULL) {
            printf("%d   ", ptr->data);
            ptr = ptr->next;
        }
        printf("\n");
    }
}
 
// Driver code
int main()
{
    push(2);
    push(5);
    push(10);
    printstack();
    topelement();
    stacksize();
    pop();
    printf("\nElement popped from the stack \n");
    topelement();
    pop();
    printf("\nElement popped from the stack \n");
    stacksize();
    return 0;
}

// A complete working java program to
// demonstrate all stack operations using
// a doubly linked list
 
class GFG {
 
  static class Node {
    int data;
    Node prev;
    Node next;
  };
 
  static Node start = null;
  static Node top = null;
 
  // Check if stack is empty
  public static boolean isEmpty() {
    if (start == null)
      return true;
    return false;
  }
 
  // pushes element onto stack
  public static void push(int d) {
    Node n;
    n = new Node();
    n.data = d;
    if (isEmpty()) {
      n.prev = null;
      n.next = null;
 
      // As it is first node if stack
      // is empty
      start = n;
      top = n;
    } else {
      top.next = n;
      n.next = null;
      n.prev = top;
      top = n;
    }
  }
 
  // Pops top element from stack
  public static void pop() {
    Node n;
    n = top;
    if (isEmpty())
      System.out.println("Stack is empty");
    else if (top == start) {
      top = null;
      start = null;
      n = null;
    } else {
      top.prev.next = null;
      top = n.prev;
      n = null;
    }
  }
 
  // Prints top element of the stack
  public static void topelement() {
    if (isEmpty())
      System.out.println("Stack is empty");
    else
      System.out.println("The element at top of the stack is : " + top.data);
  }
 
  // Determines the size of the stack
  public static void stacksize() {
    int c = 0;
    if (isEmpty())
      System.out.println("Stack is empty");
    else {
      Node ptr = start;
      while (ptr != null) {
        c++;
        ptr = ptr.next;
      }
    }
    System.out.println("Size of the stack is : " + c);
  }
 
  // Determines the size of the stack
  public static void printstack() {
    if (isEmpty())
      System.out.println("Stack is empty");
    else {
      Node ptr = start;
      System.out.print("Stack is :  ");
      while (ptr != null) {
        System.out.print(ptr.data + " ");
        ptr = ptr.next;
      }
      System.out.println("");
    }
  }
 
  // Driver code
  public static void main(String args[]) {
    push(2);
    push(5);
    push(10);
    printstack();
    topelement();
    stacksize();
    pop();
    System.out.println("\nElement popped from the stack ");
    topelement();
    pop();
    System.out.print("\nElement popped from the stack \n");
    stacksize();
  }
}
 
// This code is contributed by Saurabh Jaiswal

Stack is :  2   5   10   
The element at top of the stack is : 10   
Size of the stack is : 3 
 
Element popped from the stack 
The element at top of the stack is : 5   

Element popped from the stack 
Size of the stack is : 1