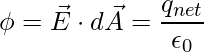El estudio de las cargas eléctricas en reposo es el tema de la electrostática . Al formar un campo eléctrico, la carga eléctrica afecta las propiedades del entorno circundante. El campo eléctrico es una propiedad de un sistema de carga. Karl Friedrich Gauss (1777-1855), uno de los más grandes matemáticos de todos los tiempos, desarrolló la ley de Gauss, que expresa la conexión entre carga eléctrica y campo eléctrico. En eso, representa el vínculo entre el campo eléctrico y la carga eléctrica, la ley de Gauss es equivalente a la ley de Coulomb. La ley de Gauss brinda un enfoque comparable para determinar expresiones de intensidad eléctrica.
¿Qué es la ley de Gauss?
La ley de Gauss, a menudo conocida como el teorema del flujo de Gauss o el teorema de Gauss, es la ley que describe la relación entre la distribución de carga eléctrica y el campo eléctrico consiguiente.
De acuerdo con la ley de Gauss, la cantidad total de flujo eléctrico que viaja a través de cualquier superficie cerrada es proporcional a la carga eléctrica contenida. El campo eléctrico de una superficie se determina mediante la ecuación de Coulomb, pero la ley de Gauss es necesaria para calcular la distribución del campo eléctrico en una superficie cerrada. Describe la carga eléctrica contenida dentro de la superficie cerrada o la carga eléctrica existente dentro de la superficie cerrada cerrada.
El flujo total contenido dentro de una superficie cerrada es igual a 1/ε 0 veces la carga eléctrica total encerrada por la superficie cerrada, de acuerdo con la Ley de Gauss.
La carga total encerrada en una superficie cerrada es proporcional al flujo total encerrado por la superficie, según el teorema de Gauss. Por lo tanto, si φ es el flujo total y ε 0 es la constante eléctrica, la carga eléctrica total Q encerrada por la superficie es,
Q = φ ε 0
Por lo tanto, la fórmula de la ley de Gauss se expresa en términos de carga como,
φ = Q / ε 0
dónde,
- Q es la carga total dentro de la superficie dada, y
- ε 0 es la constante eléctrica.
El flujo neto a través de una superficie cerrada es proporcional a la carga neta en el volumen rodeado por la superficie cerrada.
Campo eléctrico debido a una hoja plana infinita uniformemente cargada

El campo eléctrico generado por la hoja de carga infinita será perpendicular al plano de la hoja. Considere una superficie Gaussiana cilíndrica cuyo eje es perpendicular al plano de la hoja. La ley de Gauss se puede utilizar para calcular el campo eléctrico
.
Según la Ley de Gauss:
φ = Q / ε 0 …..(1)
La carga q será σA como resultado de la distribución continua de carga . Solo consideraremos el flujo eléctrico desde los dos extremos de la superficie gaussiana hipotética cuando discutamos el flujo eléctrico neto. Esto se debe al hecho de que el área de la superficie curva y el campo eléctrico son perpendiculares entre sí, lo que da como resultado un flujo eléctrico cero. Como resultado, el flujo eléctrico neto será:
φ = EA – (-EA) = 2EA
Por lo tanto, de la ecuación (1):
2EA = Q / ε 0
Al reorganizar para E as,
E = Q / 2ε 0
Campo eléctrico debido a una hoja plana infinita uniformemente cargada

Considere el radio «R» y la capa esférica delgada de la densidad de la carga superficial. La concha presenta simetría esférica, como se puede apreciar al observarla. El campo eléctrico producido por la capa esférica se puede medir de dos maneras:
- Campo eléctrico fuera de la capa esférica
- Campo eléctrico dentro de la capa esférica
Campo eléctrico fuera de la capa esférica:
Considere un punto P fuera de la capa esférica a una distancia r del centro de la capa esférica para determinar un campo eléctrico fuera de la capa. Usamos una superficie esférica gaussiana con radio r y centro O para la simetría. Debido a que todos los puntos están igualmente espaciados “r” desde el centro de la esfera, la superficie gaussiana pasará por P y experimentará un campo eléctrico constante alrededor. Entonces, según la ley de Gauss:
φ = q / ε 0
Dado que una carga está encerrada dentro de la superficie esférica gaussiana q, que es igual a σ × 4 πR 2 . Por lo tanto,
φ = σ × 4 πR 2 / ε 0 …..(1)
El flujo eléctrico total a través de la superficie gaussiana será:
φ = mi × 4 πr 2
Así que de la ecuación (1):
σ × 4 πR 2 / ε 0 = mi × 4 πr 2
o
mi = σ R 2 / ε 0 r 2
Dado que, la densidad de carga superficial, σ es q / 4 πR 2 .
mi = kq / r 2
Campo eléctrico dentro de la capa esférica:
Para encontrar el campo eléctrico dentro de la capa esférica, considere un punto P dentro de la capa. Seleccionamos la superficie gaussiana esférica que viaja a través de P, con centro en O y radio r por simetría. Ahora, de acuerdo con la ley de Gauss,
φ = q / ε 0
Dado que el flujo eléctrico total dentro de la superficie gaussiana será:
φ = mi × 4 πr 2 = 0
Por eso,
mi = 0
Problemas de muestra
Problema 1: Un cilindro largo y delgado de 1 cm de radio que lleva una carga de 5 μC/m se mantiene en agua. Encuentre la intensidad del campo eléctrico en un punto situado a una distancia de 10 cm del eje del cilindro si está sumergido en agua. (k agua = 81)
Solución:
Dado que,
q = 5 μC/m = 5 × 10 -6 C/m
R = 1 cm = 10 -2 m
r = 10 m = 10 -1 m
k agua = 81
La intensidad del campo eléctrico en un punto fuera del cilindro conductor cargado es,
mi = q / 2πkε 0 r
= 2q / 4πε 0 r
= (1 / 4πε 0 ) × q / kr
= 9 × 10 9 × (2 × 5 × 10 -6 / 81 × 10 -1 )
= 1.111 × 10 4 N/C
Problema 2: Un cilindro largo de 2 cm de radio lleva una carga de 5 µC/m mantenida en un medio de constante dieléctrica 10. Hallar la intensidad del campo eléctrico en un punto situado a 1 m de distancia del eje del cilindro.
Solución:
Dado que,
R = 2 cm
σ = 5 μC/m
k = 10
r = 1 metro
Ya que,
mi = (1 / 4πε 0 ) × q / kr
= 9 × 10 9 × (2 × 5 × 10 -6 / 10 × 1)
= 9 × 10 3 V/m
Problema 3: Una gran lámina plana de carga con una densidad de carga superficial de 5 × 10 -6 C / m 2 ) se encuentra en el aire. Encuentre la intensidad del campo eléctrico cerca de la lámina.
Solución:
Dado que,
σ = 5 × 10 -6 C/m 2
ε 0 = 8,85 × 10 -2 C 2 /Nm 2
k = 1
La intensidad del campo eléctrico cerca de la hoja es,
mi = σ / 2kε 0
= 5 × 10 -6 / (2 × 1 × 8,85 × 10 -12 )
= 2.824 × 10 5 N/C
Problema 4: Un cilindro uniformemente cargado de 10 cm de largo tiene una carga de un microculombio. Si está en un medio de constante dieléctrica 5, encuentre la intensidad en un punto fuera del cilindro. La distancia del punto al eje del cilindro es igual a su longitud.
Solución:
Dado que,
ε 0 = 8,85 × 10 -12 C 2 / Nm 2
largo = 10 cm = 0,1 m
Q = 1 μC = 10 -6 C
k = 5
r = l = 0,1 m
La densidad de carga lineal es,
q = q / l
= 10 -6 / 0,1
= 10 -5 C/m
La intensidad del campo eléctrico es,
mi = (1 / 4πε 0 ) × q / kr
= 9 × 10 9 × (2 × 10 -5 / 5 × 10 -1 )
= 3,6 × 10 5 V/m
Problema 5: Encuentre la carga superficial de una hoja plana grande de carga que tiene una intensidad de campo eléctrico cerca de la hoja de 2.8 × 10 5 N/C, mantenida en el aire. (k aire = 1)
Solución:
Dado que,
k aire = 1
E = 2,8 × 10 5 N/C
ε 0 = 8,85 × 10 -2 C 2 /Nm 2
mi = σ / 2kε 0
2,8 × 10 5 N/C = σ × (2 × 8,85 × 10 -2 )
= 4,95 × 10 -6 C /m 2
Publicación traducida automáticamente
Artículo escrito por lunaticgemini2510 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA