Diferencia entre Diffie-Hellman y RSA

La Seguridad Cibernética es la rama de las computadoras que se ocupa de las redes y la tecnología para proteger el sistema informático de usuarios de terceros no autorizados que tienen como objetivo acceder y robar información del usuario y contribuir a causar daños al sistema. La ciberseguridad tiene como objetivo adoptar las mejores prácticas para salvar computadoras/portátiles/móviles de cualquier tipo de ciberataque.

Diffie-Hellman y RSA son algoritmos de seguridad que son esenciales para proteger la información de usuarios no autorizados. son los encargados de cifrar la información y de impedir que usuarios no autorizados accedan o abran los contenidos/información. Aseguran que los contenidos cibernéticos sean seguros y que tanto el remitente como el receptor tengan derecho a acceder a la información. No, terceros o usuarios no autorizados pueden acceder a la información a la que no están destinados.

Diffie-Hellman es un algoritmo de seguridad con una sola clave privada que utilizan tanto el cliente como el servidor, es decir, la clave la comparten el cliente y el usuario. Diffie-Hellman utiliza métodos exponenciales para la generación de claves. Aquí, la clave exponencial se genera elevando números a una potencia específica. Las técnicas de cifrado y descifrado adoptadas por Diffie-Hellman son diferentes. Diffie-Hellman usa la misma clave para cifrar y descifrar.

Diffie-Hellman solo permite el acceso a las claves a personas autorizadas. Las llaves se mantienen seguras y no se transmiten a través del cable de comunicación. Diffie-Hellman es vulnerable a los logaritmos discretos, que pueden dañar la seguridad del algoritmo Diffie-Hellman.

Para obtener más detalles, consulte Aplicaciones y limitaciones del algoritmo Diffie-Hellman .

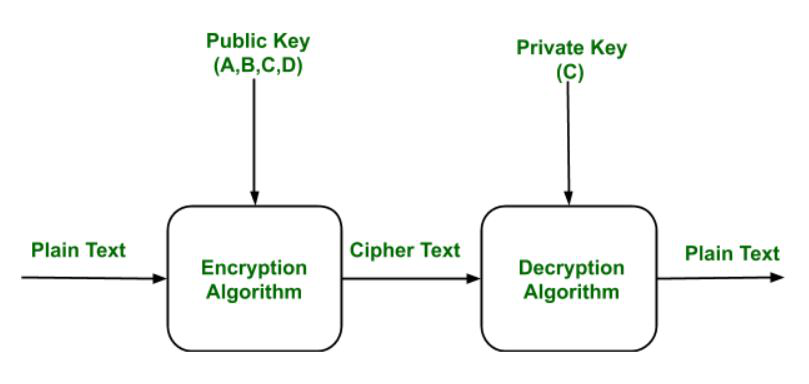
RSA es un algoritmo de seguridad con dos claves diferentes: una clave pública y otra privada que están presentes con el cliente y el servidor. Las claves aquí están separadas como claves públicas y privadas y no se comparten entre el cliente y el servidor. RSA utiliza métodos criptográficos para la generación de claves, lo que los hace extremadamente seguros y difíciles de descifrar por parte de los piratas informáticos. Una característica importante aquí es que hay claves separadas para el cifrado y descifrado de RSA. Dado que RSA tiene claves diferentes para el cifrado y el descifrado, se denomina cifrado asimétrico.

RSA sigue la regla de cifrado que debe realizar cualquier persona, pero solo los usuarios autorizados para realizar la actividad de descifrado. RSA garantiza una comunicación segura al autenticar a los usuarios y toda la comunicación y el intercambio de claves se realiza a través de un canal seguro, lo que convierte a RSA en un algoritmo seguro/confiable. RSA es vulnerable a la factorización de enteros que puede dañar la seguridad del algoritmo RSA.

Para obtener más detalles, consulte Algoritmo RSA en criptografía y Formulario completo RSA .

Diferencia entre Diffie-Hellman Key Exchange y RSA:

S. No.	Característica	Diffie-Hellman	RSA
1.	Claves Tipo de Algoritmo	Utiliza una clave privada.	Utiliza una clave pública y una privada.
2.	Generación de clave de algoritmo	Utiliza métodos exponenciales.	Utiliza métodos criptográficos.
3.	Técnicas de cifrado y descifrado	Cifrado de clave simétrica adoptado.	Cifrado de clave asimétrica adoptado.
4.	Propietarios de técnicas de cifrado y descifrado	Solo permite que las personas autorizadas accedan a las claves, realicen Cifrado y Descifrado.	Cualquiera puede realizar el cifrado, pero solo los usuarios autorizados para realizar la actividad de descifrado.
5.	Autenticación y seguridad del usuario	No autentica a los usuarios que participan en el intercambio de claves.	RSA garantiza una comunicación segura al autenticar a los usuarios y toda la comunicación.
6.	Temas de seguridad	Diffie-Hellman es vulnerable a los logaritmos discretos.	RSA es vulnerable a la factorización de enteros.