El perímetro de cualquier figura se define como la suma de todos sus lados. De forma sencilla, solo necesitamos sumar todos los lados para obtener el perímetro. En este artículo trataremos qué es el perímetro, cómo encontrar el perímetro de diferentes tipos de triángulos cuando se conoce un lado, a través de algunos ejemplos simples aprenderemos más sobre cómo podemos calcular el perímetro.
Perímetro del triángulo = a + b + c (suma de todos los lados)
Donde, a, b y c son las longitudes de cada lado. La unidad del perímetro es metro(m), centímetros(cm), o dependiendo de la unidad de longitud que nos sea dada.
Perímetro del triángulo
Como se muestra arriba, el perímetro de un triángulo es la suma de los lados. Debido a los diferentes tipos de triángulos, hay ciertas modificaciones en la fórmula para hacerlos más fáciles según el tipo de triángulo. Echemos un vistazo a los diferentes tipos de fórmulas basadas en los diferentes triángulos (equilátero, isósceles, escaleno).
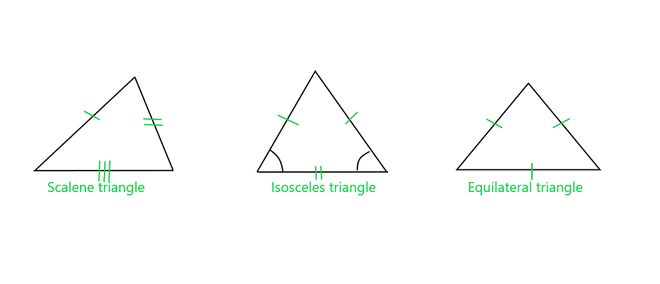
todo tipo de triangulo
- Perímetro del Triángulo Escaleno
Triángulo escaleno se define cuando todos los lados de un triángulo son diferentes, es un triángulo escaleno. Sean las unidades a, b y c los lados de un triángulo dado que ahora sabemos que en un triángulo escaleno todos son desiguales, por lo que la fórmula para el perímetro de un triángulo escaleno es,
perímetro = a + b + c
- Perímetro del Triángulo Isósceles
Triángulo isósceles se define cuando dos lados de un triángulo son iguales, es un triángulo isósceles. Sean las unidades a, b y c los lados de un triángulo dado, ahora sabemos que en el triángulo isósceles dos lados son iguales (a = b), entonces, la fórmula para el perímetro de un triángulo isósceles es,
Perímetro = a + b + c = 2a + c
- Perímetro del Triángulo Equilátero
Un Triángulo equilátero se define como cuando los lados de todos los triángulos son iguales, es un triángulo equilátero. si las unidades a, b y c son los lados de un triángulo dado, ahora sabemos que en un triángulo equilátero todos los lados son iguales, entonces, la fórmula para el perímetro de un triángulo escaleno es,
Perímetro = a + b + c = 3 × a
Pasos para Calcular el Perímetro de un Triángulo
El perímetro de cualquier triángulo se puede calcular con los siguientes pasos:
- Paso 1: Las medidas de todos los lados de un triángulo deben estar en las mismas unidades.
- Paso 2: Calcula la suma de todos los lados.
- Paso 3: luego termina respondiendo junto con su unidad.
Tomemos un ejemplo de cómo calcular el perímetro,
Ejemplo: Encuentra el perímetro de △ABC que tiene las siguientes dimensiones: AB = 3 cm, BC = 5 cm y AC = 7 cm.
Solución:
Simplemente, Perímetro del triángulo ABC = AB + BC+ AC
= 3 + 5 + 7
= 15 cm.
Hallar el perímetro de un triángulo de un solo lado
Echemos un vistazo a los diferentes conceptos para encontrar el perímetro del triángulo cuando solo se proporciona un lado del triángulo y los ángulos. La ley es conocida como la Ley de los senos,
Fórmula de la ley de los senos
Dado: △ABC
AB = c, BC = a y AC = b.
Construye una línea perpendicular a CD desde AB, CD ⊥ AB. Entonces CD = h (altura del triángulo), h separa el △ ABC en dos triángulos rectángulos, △CDA y △CDB.
Para probar: a / b = Sin A / Sin B
Prueba: En el △CDA,
Sen A = h/b (Sen ∅ = perpendicular/ hipotenusa)
Ahora en, △CDB,
Sin B = h/a
Por lo tanto,
Sin A / Sin B = (h/b)/(h/a)
= un / segundo
Por lo tanto Probado.
Del mismo modo,
y similar para cualquier par de ángulos y sus lados opuestos.
Problemas de muestra
Pregunta 1: Encuentra el perímetro del triángulo cuyos lados son 12 cm, 20 cm y 9 cm.
Solución:
Dado,
Los lados del triángulo son como: 12 cm, 20 cm, 9 cm.
Perímetro del triángulo = suma de todos los lados
= 12 + 20 + 9
= 41 centímetros
Pregunta 2: Comprueba si el triángulo es válido o no si los lados son: 12 cm, 6 cm y 3 cm.
Solución:
Un triángulo válido se define como si la suma de sus dos lados es mayor que el tercero para cada lado que debe obedecer esta regla.
- a + b > c
- a + c > b
- b + c > un
En la pregunta dada tenemos: 12 cm, 6 cm y 3 cm como lados del triángulo
6 + 3 < 12 que no obedece condición, por lo tanto no pueden ser dimensiones válidas del triángulo.
Pregunta 3: Un triángulo isósceles tiene un perímetro de 37 m y su base tiene una longitud de 9 m calcular otros lados.
Solución:
Perímetro del triángulo = 37 m
Perímetro del triángulo isósceles = 37 m
2a + c = 37
2 × 9 + c = 37
c = 37 – 18
c = 19 metros
Los otros dos lados miden 19 y 19 m respectivamente
Pregunta 4: si la altura del triángulo es de 8 cm y la base es de 4 cm, calcula su área.
Solución:
Dado:
Altura del triangulo = 8cm
Base del triangulo = 4cm
Área del triángulo = 1/2 × base × altura
= 1/2 × 8 × 4
= 16cm2
Pregunta 5: Si dos ángulos de un triángulo miden 45°, entonces calcula el tercer ángulo y también el tipo de triángulo.
Solución:
Los primeros dos ángulos son = 45°
Sabemos que la suma de los ángulos interiores del triángulo = 180°
∠1 + ∠2 + ∠3 = 180°
45° + 45° + ∠3 = 180° = > ∠3 = 180° – 90°
∠3 = 90°
Tenemos un ángulo igual al ángulo recto, esto muestra que el tipo de triángulo es el triángulo de ángulos rectos .
Pregunta 6: el perímetro de un triángulo equilátero es de 18 cm, calcule su área.
Solución:
Dado,
Perímetro del triángulo equilátero = 18 cm
3 × lado = 18
Lado = 18/3 = 6
Área del triángulo equilátero = √3/4 lado 2 = √3/4 × 6 × 6
= 9√3cm2
Pregunta 7: Calcula el perímetro de un triángulo con solo un lado dado y los ángulos son 105°, 45° y 30° y el lado dado es de 8 unidades, que es opuesto a 30°.
Solución:
Sea a la longitud del lado opuesto a los ángulos de 45 ∘ , b la longitud del lado opuesto al ángulo de 105°.
La ley de los senos es como,
8 / sen(30°) = a / sen(45°) = b / sen(105°)
sen(30°) = 0.5
pecado(45°) = 0.707107
pecado(105°) = 0.965926
8 / pecado (30°) = 16
a = 16 × sin(45°) = 11.3137
b = 16 × sin(105°) = 15,4542
Perímetro = 8 + a + b
= 34.76852
Publicación traducida automáticamente
Artículo escrito por chauhanishan82 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
