El torque es la fuerza que puede hacer que un objeto gire alrededor de un eje. La fuerza es lo que hace que un objeto se acelere en cinemática lineal. La aceleración angular también es causada por el par. Como resultado, el par se puede definir como el equivalente giratorio de una fuerza lineal. El punto en el que gira el elemento se conoce como eje de rotación. En física, el torque es la tendencia de una fuerza a girar o girar. El par se puede expresar de varias formas, incluido el momento y el momento de fuerza. En esta publicación, veremos cómo calcular el par en un bucle de alambre rectangular que transporta corriente en un campo magnético uniforme.
Par en un bucle de corriente rectangular
Considere un bucle rectangular que transporta una corriente de magnitud I. Cuando se coloca en un campo magnético, este bucle experimenta un par pero no una fuerza neta, similar a lo que experimenta un dipolo eléctrico en un campo eléctrico homogéneo. Considere el caso donde la espira rectangular está en el mismo plano que el campo magnético B. Los brazos de la espira que son paralelos a los imanes no reciben fuerza del campo, pero los brazos que son perpendiculares a los imanes reciben una fuerza igual a F 1 .
F1 = IbB
Esta fuerza está dirigida en la dirección del plano. De la misma manera, podemos escribir la fórmula de una fuerza F 2 aplicada al brazo CD.
F 2 = IbB = F 1
El momento de torsión del bucle está dado por y la fuerza neta del bucle es cero.
τ = F 1 (a/2) + F 2 (a/2)
= IbB(a/2) + IbB(a/2)
= I(ab)B
τ = BIA
El área del rectángulo es ab. El bucle gira en sentido contrario a las agujas del reloj debido al par.
Considere la situación en la que el plano de la espira no es paralelo al campo magnético. Sea el ángulo generado por el campo, y sea la normal de la bobina dada por θ. Las fuerzas que actúan sobre los brazos BC y DA siempre serán del mismo tamaño y siempre actuarán en direcciones opuestas, como puede verse. Los resultados de estas fuerzas se anulan porque son opuestos iguales y colineales en todos los puntos, lo que da como resultado fuerza o par cero. Las fuerzas sobre los brazos AB y CD están determinadas por F 1 y F 2 . Estas fuerzas son similares en tamaño y dirección y pueden ser producidas por,
F1 = F2 = IbB
Debido a que estas fuerzas no son colineales, el par en la bobina provoca un par. La magnitud del par se puede calcular usando,
τ = F 1 (a/2) sen θ + F 2 (a/2) sen θ
= I(ab)B sen θ
τ = IAB sen θ
Explicación del par en el lazo de corriente
Cuando aplica presión a un objeto, se mueve o ejerce una cierta cantidad de fuerza. Por ejemplo, girar la tapa de una botella, quitar la tapa de un paquete, abrir el pomo de la puerta, atarse los cordones de los zapatos, etc. Este es un movimiento giratorio, que es un movimiento de torsión con algo de movimiento. Si no se capta el concepto de torque, no habrá movimiento. Torque es una frase que se refiere al movimiento giratorio que tienen todos los elementos y sin el cual no podríamos operar correctamente.
La fórmula del par es τ = F × r porque el par es igual a la fuerza de torsión que tiende a inducir el movimiento o la rotación. Esta fórmula se utiliza cuando se aplica una fuerza (f) a un elemento en función de la distancia (r) entre el centro de rotación y el lugar donde se aplica la fuerza. Para detectar la dirección del par, los alumnos deben curvar los dedos de la mano derecha en la dirección de la corriente y el pulgar debe sobresalir y señalar el vector de área, de acuerdo con la regla de la mano derecha.
Torque en una ecuación de bucle de corriente rectangular en forma vectorial
Considere una bobina rectangular PQRS que cuelga de un campo de inducción B con un campo magnético uniforme. Sean PQ = RS = l y QR = SP = b las dos variables. Sea I la corriente que fluye a través de la bobina en la dirección PQRS y sea θ el ángulo que forma el plano de la bobina con la dirección del campo magnético. Las fuerzas actuarán sobre los cuatro brazos de la Espiral.
Los vectores de fuerzas F 1 y F 3 que actúan sobre los lados PQ y RS son iguales y opuestos, pero sus caminos de acción son distintos, según la regla de la mano izquierda de Fleming; por lo tanto, la fuerza resultante del vector F 1 y el vector F 3 es cero, pero forman un par conocido como par deflector . La distancia perpendicular entre el vector F 1 y el vector F 3 es bsinθ cuando el plano normal de la espira forma un ángulo con la dirección del campo magnético B.
Dado que, Torque, τ = IAB senθ
Entonces, cuando el ciclo contiene N vueltas, entonces
τ = NI ABsenθ
En forma vectorial,
La dirección del par es perpendicular a la dirección del área de la espira, así como a la dirección del campo magnético, es decir, a lo largo de
Conclusión
La bobina gira sobre su propio eje debido a este par. Su valor varía según el ángulo formado por el plano de la bobina y la dirección del campo magnético.
- Si un dipolo eléctrico está en el campo eléctrico, el par se convierte en
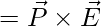 , donde, P es el momento dipolar eléctrico y E es el campo eléctrico.
, donde, P es el momento dipolar eléctrico y E es el campo eléctrico. - Si un dipolo magnético está en un campo magnético, el par se convierte en
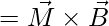 , donde M es el momento dipolar magnético y B es el campo magnético.
, donde M es el momento dipolar magnético y B es el campo magnético.
Casos especiales
Caso 1: Si la bobina es paralela a la dirección B del campo magnético,
Entonces, θ = 0 o y cos θ = 1. Tenemos,
τ = nIBA cos θ
= nIBA cos 0
= NIBA
∴ τ = nIBA (Máximo)
Caso 2: Si la bobina es perpendicular a la dirección del campo magnético B,
Entonces, θ = 90 o y cos θ = 0.
τ = nIBA cos θ
= nIBA cos 90
= NIBA (0)
∴ τ = 0 (Mínimo)
Problemas de muestra
Problema 1: ¿Cuál es el par máximo que puede crear un mango de 40 cm de ancho cuando se libera con una fuerza de 2N en su borde?
Solución:
Dado que: F = 2 N,
profundidad = 40 cm = 0,40 m
τ = F × re
= 20 × 0,40
= 8 Nm
Problema 2: Un imán de barra corta con su eje a 30 o y un campo magnético externo uniforme de 0,25 T experimenta un par de magnitud de 4,5 × 10 -2 J. ¿Qué tan grande es el momento magnético del imán?
Solución:
Dado que:
τ = 4,5 × 10 -2 J,
θ = 30 o ,
B = 0,25 T
Tenemos,
τ = MB sen θ
4,5 × 10 -2 = M × 0,25 sen 30 o
∴ M = 0,36 J/T
Problema 3: Un dipolo eléctrico con una intensidad de 2 × 10 5 N/C se coloca en un ángulo de 30 o . Experimenta un par de 4 Nm. El dipolo tiene una carga de 2 cm.
Solución:
Dado que:
E = 2 × 10 5 N/C,
τ = 4 Nm,
l = 2 cm = 0,02 m
Tenemos,
τ = pE sen θ
4 = p × 2 × 10 5 × sen θ
p = 4 × 10-5 Cm
q = p/l
q = (4 × 10 -5 )/0,02
q = 2 mC
Problema 4: En un campo magnético homogéneo de fuerza 0,8 Weber/m 2 , se suspende verticalmente una bobina rectangular de 0,56 m de largo y 0,2 m de ancho con 40 vueltas de alambre. Una corriente de 6 A fluye a través de la bobina. El par necesario para mantener la bobina en equilibrio estable será si el plano de la bobina está inclinado en un ángulo de 90 ° con la dirección del campo.
Solución:
M = NIπr2
= 40 × 6 × 0,56 × 0,2
= 26,88
B = 0,8 T
Tenemos,
τ = MB sen θ
= 26,88 × 0,8 sen 90 o
= 21,504 Nm
Problema 5: Si una puerta tiene un ancho de 80 cm y es liberada por una fuerza de 2 N en su borde, calcule el torque producido por la puerta.
Solución:
Dado que:
F = 2 N,
profundidad = 80 cm = 0,80 m
τ = F × re
= 20 × 0,80
= 16 nm
Problema 6: un imán de barra corto con su eje en 90 o y un campo magnético externo uniforme de 0,27 T experimenta un par de magnitud 2,51 × 10 2 J. ¿Cuál es el momento magnético del imán?
Solución:
Dado que:
τ = 2,51 × 10 2 J,
θ = 90 o ,
B = 0,27 T
Tenemos,
τ = MB sen θ
2,51 × 10 2 = M × 0,27 sen 90 o
M = 929 J/T
Problema 7: Obtenga una expresión de torque para una corriente rectangular que transporta una mirada en un campo magnético uniforme B. Indique de qué manera se está torqueando el bucle.
Solución:
Considere una bobina rectangular PQRS que cuelga de un campo de inducción B con un campo magnético uniforme. Sean PQ = RS = l y QR = SP = b las dos variables. Sea I la corriente que fluye a través de la bobina en la dirección PQRS y sea θ el ángulo que forma el plano de la bobina con la dirección del campo magnético. Las fuerzas actuarán sobre los cuatro brazos de la Espiral.
Los vectores de fuerzas F 1 y F 3 que actúan sobre los lados PQ y RS son iguales y opuestos, pero sus caminos de acción son distintos, según la regla de la mano izquierda de Fleming; por lo tanto, la fuerza resultante del vector F 1 y el vector F 3 es cero, pero forman un par conocido como par deflector . La distancia perpendicular entre el vector F 1 y el vector F 3 es bsinθ cuando el plano normal de la espira forma un ángulo con la dirección del campo magnético B.
Dado que, Torque, τ = IAB senθ
Entonces, cuando el ciclo contiene N vueltas, entonces
τ = NI ABsenθ
En forma vectorial,
La dirección del par es perpendicular a la dirección del área de la espira, así como a la dirección del campo magnético, es decir, a lo largo de
Publicación traducida automáticamente
Artículo escrito por bhagyashrijadhav25630 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
