Un autómata celular es un modelo discreto similar a cualquier otro autómata que tiene sus propios estados de inicio y un conjunto de reglas.
Un autómata celular es un modelo de un sistema de objetos “célula” con las siguientes características:
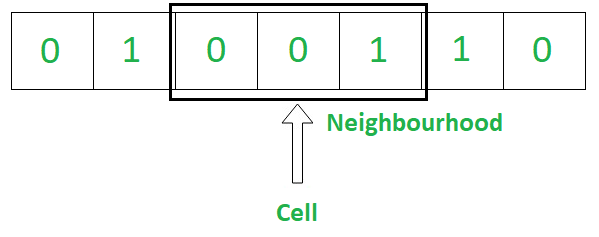
- Las células viven en una cuadrícula que puede ser unidimensional o incluso multidimensional.
- Cada celda tiene un estado. El número de posibilidades de estado es típicamente finito. El ejemplo más simple tiene las dos posibilidades de 1 y 0
- Cada celda tiene un vecindario y normalmente es una lista de celdas adyacentes
¿Principio de funcionamiento de los autómatas celulares?
El principio de funcionamiento de los autómatas celulares se muestra a continuación:
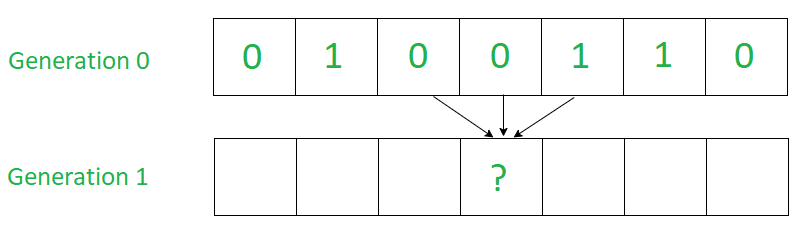
- Se selecciona un estado inicial asignando un estado para cada celda.
- Se crea una nueva generación, de acuerdo con alguna regla fija que determina el nuevo estado de cada celda en términos de:
- El estado actual de la celda.
- Los estados de las células en su vecindad.
- Por lo tanto, un nuevo estado se calcula observando todos los estados vecinos anteriores.
Ejemplos de autómatas celulares:
1. El juego de la vida de Conway
2. Regla 90:
La regla 90 es un autómata celular elemental que consta de una array unidimensional de celdas, cada una de las cuales puede contener un valor 0 o 1. Cada celda es el exclusivo o (XOR) de sus dos vecinos.
| Estado actual | 111 | 011 | 101 | 100 | 011 | 010 | 001 | 000 |
| Estado siguiente | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 |
Si concatenamos el siguiente estado en un solo número binario y lo convertimos a decimal (01011010) 2, se convierte en 90, por lo que obtenemos el nombre de Regla 90.
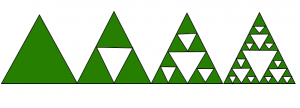
3. Cuando el estado inicial tiene una sola celda distinta de cero, este diagrama tiene la apariencia del triángulo de Sierpiński .
Implementación del triángulo de Sierpiński:
C++
// C++ code to implement Sierpinski Triangle
#include <bits/stdc++.h>
using namespace std;
// Length of the string used as a "Seed"
#define LENGTH 34
// How many lines the program will generate
int n = 15;
// All the patterns possible
vector<vector<int> > rules = { { 0, 0, 0 }, { 0, 0, 1 },
{ 0, 1, 0 }, { 0, 1, 1 },
{ 1, 0, 0 }, { 1, 0, 1 },
{ 1, 1, 0 }, { 1, 1, 1 } };
// Utility Function to Print Rules
void printRules()
{
int i, j;
cout << "The rules of Rule 90 Cellular Automaton"
" are as follows: \n";
for (i = 0; i < 8; i++) {
cout << "\t\tRule " << i + 1 << ": ";
for (j = 0; j < 3; j++)
cout << rules[i][j] << " ";
cout << "-> sets cell to: "
<< (rules[i][0]
^ rules[i][2]) << "\n";
}
}
// Print the Current State
void outState(vector<int> s)
{
cout << "\t\t";
for (int i = 0; i < LENGTH; i++) {
if (s[i] == 1)
cout << "\u25A0";
else if (s[i] == 0)
cout << " ";
}
cout << "\n";
}
// Function to print the triangle
void utilize()
{
// Initialize starting state
// to sierpinski triangle
vector<int> sierpinski(LENGTH);
vector<int> updateState(LENGTH);
sierpinski[(LENGTH) / 2 - 1] = 1;
// Print Sierpinski Triangle
// initial String
outState(sierpinski);
// Loop to generate/update the state
// and update state arrays
for (int i = 0; i < n; i++)
{
// Erase the old state
updateState.assign(LENGTH, 0);
// Create the new state
for (int j = 1; j < LENGTH - 1; j++)
{
int f1 = sierpinski[j - 1];
int f2 = sierpinski[j];
int f3 = sierpinski[j + 1];
// Create an array with the
// current pattern
vector<int> current;
current.push_back(f1);
current.push_back(f2);
current.push_back(f3);
// XOR the current state's neighbours
// to set the cell's value
// in Update State
updateState[j] = current[0] ^ current[2];
}
// Update the current state
sierpinski.assign(updateState.begin(),
updateState.end());
// Print the new current state
outState(sierpinski);
}
}
// Driver code
int main()
{
// Print out the rules for
// rule 90 cellular Automaton
printRules();
cout << "\n\t\t\tSIERPINSKI TRIANGLE\n\n";
utilize();
return 0;
}
The rules of Rule 90 Cellular Automata are as follows:
Rule 1: 0 0 0 -> sets cell to: 0
Rule 2: 0 0 1 -> sets cell to: 1
Rule 3: 0 1 0 -> sets cell to: 0
Rule 4: 0 1 1 -> sets cell to: 1
Rule 5: 1 0 0 -> sets cell to: 1
Rule 6: 1 0 1 -> sets cell to: 0
Rule 7: 1 1 0 -> sets cell to: 1
Rule 8: 1 1 1 -> sets cell to: 0
SIERPINSKI TRIANGLE
■
■ ■
■ ■
■ ■ ■ ■
■ ■
■ ■ ■ ■
■ ■ ■ ■
■ ■ ■ ■ ■ ■ ■ ■
■ ■
■ ■ ■ ■
■ ■ ■ ■
■ ■ ■ ■ ■ ■ ■ ■
■ ■ ■ ■
■ ■ ■ ■ ■ ■ ■ ■
■ ■ ■ ■ ■ ■ ■ ■
■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■ ■