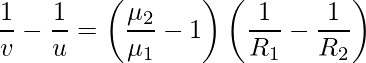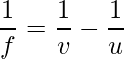La luz es un tipo de energía que se puede ver a simple vista. Observamos objetos y entendemos el mundo que nos rodea principalmente a través del uso de la luz. La luz viaja en un camino recto a una velocidad extremadamente rápida de alrededor de 3 × 10 8 ms. Una pequeña fuente de luz produce una fuerte sombra sobre un objeto opaco. Esto significa que la luz viaja en línea recta y la ruta se denomina rayo de luz, y una agrupación de rayos se denomina haz de luz.
Un rayo de luz indica la dirección de propagación de la luz. Cuando la luz golpea una superficie entre dos medios transparentes, se refleja y se refracta, lo que hace que los rayos de luz se desvíen. Los rayos de luz también se curvan alrededor del borde de la obstrucción, aunque la curvatura es relativamente mínima debido a la longitud de onda muy corta de la radiación de luz. Esto se conoce como difracción de la luz.
Ecuación del fabricante de lentes
La distancia de la imagen se puede calcular utilizando la fórmula de la lente y el conocimiento de la distancia del objeto y la distancia focal. La fórmula de la lente describe la relación entre la distancia de una imagen I la distancia de un objeto (o) y la distancia focal (f) de la lente en óptica. La fórmula de la lente funciona tanto para lentes convexas como cóncavas.
La ecuación de la lente es utilizada por los fabricantes de lentes para crear lentes con las distancias focales deseadas. Lentes con distancias focales variables se emplean en una variedad de dispositivos ópticos. La distancia focal de una lente está determinada por los radios de curvatura de dos superficies y el índice de refracción del material de la lente.
Considere una lente de vidrio delgada con un índice de refracción de μ 2 y centros de curvatura C 1 y C 2 con radios de curvatura R 1 y R 2 . Sea μ 1 el índice de refracción del medio circundante. Cuando un objeto puntual ‘O’ se mantiene en el eje a una distancia u de la lente, el rayo OP pasa a través del centro óptico sin desviación. Si el otro rayo OA no hubiera sido refractado junto con AB por la primera superficie, habría llegado al punto I’. Si la segunda superficie no existiera. Pero, debido a la segunda superficie, el rayo sufre otra refracción en el punto B y llega al punto I.

Refracción a través de una lente convexa
Para la primera refracción, la distancia al objeto es u y la distancia a la imagen es v’. Usando la relación entre uv μ 1 y R para la refracción en una sola superficie curva (convexa).
……(1)
Para la segunda refracción, I’ actúa como un objeto virtual en el medio de la lente de índice de refracción μ 2 , para producir una imagen final en I en el medio circundante de índice de refracción μ 1. Usando la relación entre uv μ 1 y R para la refracción en una sola superficie curva (convexa).
……(2)
Sumando la Ecuación (1) y (2), obtenemos
……(3)
- Caso 1: Si el objeto puntual está en el infinito, su imagen se forma en el punto focal. es decir, si u = ∞, entonces v = f; por lo tanto, la ecuación (3) se convierte en-
……(4)
Esta es la ecuación del fabricante de lentes . La lente de cualquier distancia focal deseada se puede producir eligiendo los valores adecuados de R 1 , R 2 , μ 1 , μ 2.
- Caso 2: Cuando la lente se mantiene en un medio de aire, μ 1 = 1 y la ecuación (4) se convierte en –
……(5)
Usando la nueva convención de signos cartesianos, obtenemos una distancia focal positiva para la lente convexa y una distancia focal negativa para la lente cóncava.
Comparando la ecuación (3) y (5), obtenemos
Esta es la fórmula de la lente, que se utiliza para encontrar prácticamente la distancia focal de una lente dada.
Aumento
La ampliación significa hacer que los objetos parezcan más grandes de lo que son. Los siguientes son los diferentes casos para determinar la magnificación para diferentes casos como:
Aumento producido por una lente (m)
El aumento (m) de una lente se define como la relación entre la altura de una imagen y la altura de un objeto.
m = Altura de la imagen / Altura del objeto
m = h yo / h o
También se presenta en términos de distancia de la imagen y distancia del objeto.
m = Distancia de la imagen / Distancia del objeto
m = v / tu
Es equivalente a la relación de distancia imagen-objeto.
*** QuickLaTeX cannot compile formula: *** Error message: Error: Nothing to show, formula is empty
Ampliación producida por una lente convexa
Conocemos las propiedades de la lente convexa que es virtual y vertical. Debido a que una lente convexa puede crear imágenes tanto virtuales como reales, la ampliación producida por una lente convexa puede ser positiva o negativa. La ampliación es beneficiosa para las imágenes virtuales pero perjudicial para las imágenes reales. es decir, Positivo (+ve) para la imagen virtual y Negativo (-ve) para la imagen real.
Caso 1: si la magnitud del aumento es menor que uno, significa que la imagen es más pequeña que el objeto. |m|<1 , la imagen se reduce .
Caso 2: si la magnitud del aumento es mayor que uno, entonces la imagen es más grande que el objeto.
|m|>1 , la imagen se amplía .
Caso 3: si la magnitud del aumento es uno, entonces la imagen tiene el mismo tamaño que un objeto. |m| = 1 , la imagen tiene el mismo tamaño que el objeto.
Aumento por una lente cóncava
Cuando el elemento está frente a la lente cóncava, la imagen está frente al mismo objeto en el mismo lado. La lente cóncava siempre produce una imagen virtual, erecta y reducida. Debido a que las lentes cóncavas siempre generan imágenes virtuales , el aumento logrado por ellas siempre es positivo y siempre produce una imagen que es más pequeña que el objeto.
La magnitud del aumento es menor que uno, por lo que la imagen es más pequeña que el objeto.
|m|<1 , la imagen se reduce.
A continuación, la representación tabular indica el aumento y la naturaleza de la imagen para diferentes casos para diferentes lentes como:
|
Lente |
Propiedades |
Distancia del objeto (u) |
Distancia de la imagen (v) |
Magnitud en términos de ‘u’ y ‘v’ |
Magnitud en términos de altura de la imagen y altura del objeto |
|
|
Lentes convexas |
Las imágenes producidas son virtuales y vertical (imagen real) |
-ve |
Imagen virtual: -ve Imagen real: + ve |
Imagen virtual: +ve Imagen real: -ve |
|m|=1 |m|<1 |m|>1 |
cuando h i = h o cuando hola < ho cuando h i > h o |
|
Cóncavo |
La imagen producida es siempre virtual. |
-ve |
-ve |
Imagen virtual: +ve |
|m|<1 |
– |
Ejemplos de preguntas
Pregunta 1: Si una lente delgada se sumerge en agua, ¿cambiará su distancia focal?
Responder:
La distancia focal de una lente está determinada por el índice de refracción del material de la lente en relación con su entorno, según lo determina la fórmula del fabricante de la lente.
Cuando una lente delgada se sumerge en agua, su índice de refracción relativo disminuye y, por lo tanto, su distancia focal aumenta (y la potencia de la lente disminuye).
Sea f a la distancia focal de una lente de vidrio delgada en el aire y f w las distancias focales de una lente de vidrio delgada en el agua.
Sean a μ g y w μ g = a μ g / a μ w los índices de refracción relativos del vidrio con respecto al aire y al agua.
Después,
Dividiendo ambas ecuaciones obtenemos,
Ya que, a μ g > w μ g , f w > f a
Pregunta 2: ¿Defina la distancia focal de una lente, dé signos de la distancia focal de la lente cóncava y convexa?
Responder:
La distancia focal de una lente es la distancia entre su centro óptico y su foco principal.
Se define como la distancia entre el centro óptico y el segundo foco primario, de manera que la distancia focal de una lente convexa es positiva y la de una lente cóncava es negativa.
Pregunta 3: ¿Qué es el aumento lineal producido por una lente? ¿Cuál es el significado de su signo?
Responder:
- El aumento lineal producido por una lente es el factor por el cual el tamaño de la imagen cambia con respecto al tamaño del objeto.
Se define como la relación entre la altura de una imagen y la altura de un objeto.
m = Altura de la imagen / Altura del objeto
m = hola / hola
- El indicador de ampliación lineal especifica si la imagen está derecha o invertida en relación con el objeto. El aumento de una imagen vertical es positivo, mientras que el aumento de una imagen invertida es negativo.
Problemas de muestra
Problema 1: Los radios de curvaturas de una lente convexa son 40cm y 50cm, calcule la distancia focal si el índice de refracción de su material es 2.1.
Solución:
Dado que: Índice de refracción (μ) = 2,1
Radios R 1 = 40 cm
Radios R 2 = -50cm (convenciones de signos)
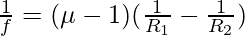
= (2.1 – 1) (1/40 – 1/(-50))
= 1,1 × 9 / 200
= 0.0495
1 / f = 1 / 0,0495
= 20,2020cm
La distancia focal de la lente convexa es de 20,2020 cm.
Problema 2: Una lente convexa forma una imagen real e invertida de un objeto a 40cm de la lente. ¿Dónde se colocará el objeto frente a la lente convexa, si la imagen es del mismo tamaño que el objeto?
Solución:
Dado que: Distancia de la imagen (v) = 40cm
El tipo de lente es convexo y la imagen es una imagen real
La altura de la imagen es del mismo tamaño que el objeto, es decir, h i = -h o
Ya que, aumento (m) = h i / h o = v / u
= -h o / h o = v / u
v/u = -1
tu = -1 × v
tu = -40cm.
1/f = 1/v -1/u
= 1/40 – 1/(-40)
= 2/40
1/f = 1/20
f = 20 cm = 0,2 m
El objeto se coloca a 40 cm de distancia de la lente convexa.
Problema 3: una lente cóncava de distancia focal de 20 cm forma una imagen de una aguja a 15 cm de la lente. ¿A qué distancia se coloca la aguja de la lente?
Solución:
Dado que:
Distancia focal (f) = -20cm
Distancia de la imagen (v) = -15 cm
1/f = 1/v – 1/u
o
1/u = 1/v – 1/f
= 1/(-15) – (1/-20)
= -20 + 15 / 300
= – (1/60)cm
tu = -60cm
El objeto se coloca 60 cm delante de la lente cóncava.
Problema 4: una lente cóncava de vidrio tiene una distancia focal de 20 cm en el aire. Encuentre su distancia focal cuando se sumerge en agua. Dado que el índice de refracción de la lente de vidrio es 1,5 y el del agua es 4.
Solución:
Sea f a la distancia focal de la lente en el aire
Sea f w la distancia focal de la lente en el agua.
Dado que:
f a = – 20cm (lente cóncava)
un µg = 1,5
un μ w = 4
w μ gramo = un μ gramo / un μ w
= (3/2) / (4/1)
= 3/8
Dividiendo la ecuación ambas ecuaciones obtenemos,
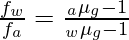
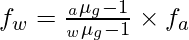
= (1,5 – 1) / (0,375 – 1) × (-20)
= 0,5 / (-0,625) × (-20)
f ancho = 16 cm
Problema 5: Un sistema óptico utiliza dos lentes delgadas convexas en contacto que tienen una distancia focal efectiva de 30/4 cm. Si una de las lentes tiene una distancia focal de 30 cm, encuentre la distancia focal de la otra.
Solución:
Dado que:
f = 30/4cm
f 1 = 30 cm
1/f = 1/f 1 + 1/f 2
1/f 2 = 1/f – 1/f 1
= 1/(30/4) – 1/30
= 4/30 – 1/30
1/f2 = 1/10
La distancia focal de la otra lente, f 2 es igual a 10 cm.
Publicación traducida automáticamente
Artículo escrito por lunaticgemini2510 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA