Muestre que el producto de z̄ = r[cos(-θ) + isin(-θ)] y z = r[cosθ + isinθ] es igual al cuadrado del módulo

Los números complejos son la suma de las partes real e imaginaria, representadas generalmente como a + ib, donde i se denomina parte imaginaria y es la raíz cuadrada de −1. Aprendamos en detalle el módulo y el argumento de un número complejo para resolver problemas relacionados con ellos,

Módulo y argumento de un número complejo

Cuando se presenta un número complejo en un gráfico, su parte real se representa en el eje x y la parte imaginaria en el eje y. Digamos que si el número fuera representado por el punto P en la figura que se muestra a continuación, los triángulos OPA y OPB serían ambos rectángulos. Claramente, en el triángulo rectángulo POA, PO es la hipotenusa; Oa es la base y Pa es la perpendicular. Usando el Teorema de Pitágoras, tenemos:

OP ² = AO ² + PA ²

OP = 

El valor absoluto de un número complejo se considera su módulo. Es la raíz cuadrada de la suma de los cuadrados de sus partes real e imaginaria. En el caso anterior, OP es el módulo del número complejo de la forma z = a + ib, y se denota por r.  

El argumento de un número complejo se define como el ángulo en el que la gráfica del número se inclina hacia el eje real. El argumento de un número complejo de la forma z = a + ib se da como:

θ =   = π/4.

Demuestre que el producto de z̄ = r[cos(-θ) + isin(-θ)] y z = r[cosθ + isinθ] es igual al cuadrado del módulo.

Solución:

Módulo de z = r[cosθ + isinθ] = r.

Cuadrado de módulo = r ²

Dado: z bar = r[cos(−θ) +isin(−θ)] = r[cosθ − isinθ]

Ahora, r[cosθ − isinθ] × r[cosθ + isinθ] = r ² [cos ² θ − i ² sen ² θ]

= r ² [cos ² θ − (−1)sen ² θ]

= r ² [cos ² θ + sen ² θ]

Usando cos ² θ + sen ² θ = 1, tenemos:

z × z̄ = r ²

Por lo tanto probado.

Problemas similares

Pregunta 1: Encuentra el módulo y el argumento de 1 + i.

Solución:

a = 1, b = 1

Módulo = 

=  

= √2

Argumento = tan-1[1/1]

= tan-1[π/4]

= π/4

Pregunta 2: Encuentra el módulo y el argumento de -3 – 3i.

Solución:

a = -3, b = -3

Módulo = 

=   

= 3√2

Argumento = tan-1[b/a]

= tan-1[3/3]

= π/4

Pregunta 3: Encuentra el módulo y el argumento de 2i.

Solución:

a = 0, b = 2

Módulo =   

=   

= √4

= 2

Argumento = tan-1[2/0]

= π/2

Pregunta 4: Encuentra el módulo y el argumento de -4.

Solución:

a = -4, b = 0

Módulo = 

=  

= √16

= 4

Argumento = tan-1[0/4]

= π

Pregunta 5: Encuentra el módulo y el argumento de -1 + 2i.

Solución:

a = -1, b = 2

Módulo =   

=   

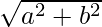
= √5

Argumento = tan-1[2/1]

= bronceado ^-1 2