hashing | Conjunto 3 (direccionamiento abierto)

• Insertar (k): Continúe sondeando hasta que encuentre una ranura vacía. Una vez que encuentre una ranura vacía, inserte k. 
• Buscar (k): siga sondeando hasta que la clave de la ranura no sea igual a k o se alcance una ranura vacía. 
• Eliminar (k) : la operación de eliminación es interesante . Si simplemente eliminamos una clave, entonces la búsqueda puede fallar. Por lo tanto, las ranuras de claves eliminadas se marcan especialmente como «eliminadas». 
  La inserción puede insertar un elemento en un espacio eliminado, pero la búsqueda no se detiene en un espacio eliminado. 

El direccionamiento abierto se realiza de las siguientes maneras: 

a) Sondeo lineal: 

En el sondeo lineal, la tabla hash se busca secuencialmente desde la ubicación original del hash. Si en caso de que la ubicación que obtengamos ya esté ocupada, buscamos la siguiente ubicación. 
La función utilizada para el refrito es la siguiente: rehash(clave) = (n+1)%table-size. Por ejemplo, la brecha típica entre dos sondas es 1, como se ve en el siguiente ejemplo. 
Sea hash(x) el índice de ranura calculado usando una función hash y S el tamaño de la tabla 

If slot hash(x) % S is full, then we try (hash(x) + 1) % S
If (hash(x) + 1) % S is also full, then we try (hash(x) + 2) % S
If (hash(x) + 2) % S is also full, then we try (hash(x) + 3) % S 
..................................................
..................................................

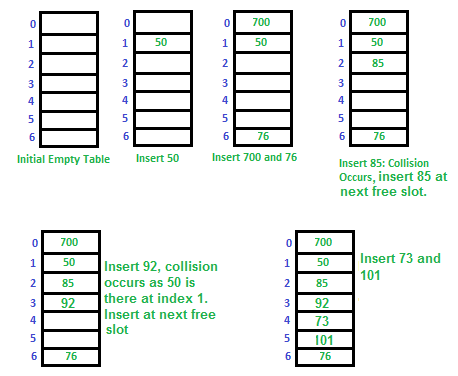
Consideremos una función hash simple como «key mod 7» y una secuencia de teclas como 50, 700, 76, 85, 92, 73, 101. 

Desafíos en el sondeo lineal:

1. Agrupamiento primario: uno de los problemas con el sondeo lineal es el agrupamiento primario, muchos elementos consecutivos forman grupos y comienza a tomar tiempo encontrar un espacio libre o buscar un elemento.  
2. Agrupamiento secundario : el agrupamiento secundario es menos severo, dos registros solo tienen la misma string de colisión (Secuencia de sonda) si su posición inicial es la misma.

b) Sondeo cuadrático Si observa detenidamente, comprenderá que el intervalo entre sondeos aumentará proporcionalmente al valor hash. El sondeo cuadrático es un método con la ayuda del cual podemos resolver el problema de la agrupación que se discutió anteriormente. Este método también se conoce como método del cuadrado medio. En este método buscamos i ² ‘ésima ranura en i’ésima iteración. Siempre comenzamos desde la ubicación original del hash. Si solo la ubicación está ocupada, verificamos las otras ranuras.

let hash(x) be the slot index computed using hash function.  
If slot hash(x) % S is full, then we try (hash(x) + 1*1) % S
If (hash(x) + 1*1) % S is also full, then we try (hash(x) + 2*2) % S
If (hash(x) + 2*2) % S is also full, then we try (hash(x) + 3*3) % S
..................................................
..................................................

c) Hashing doble Los intervalos que se encuentran entre las sondas se calculan mediante otra función hash. El hash doble es una técnica que reduce la agrupación en clústeres de forma optimizada. En esta técnica, los incrementos de la secuencia de sondeo se calculan utilizando otra función hash. Usamos otra función hash hash2(x) y buscamos la ranura i*hash2(x) en la i-ésima rotación. 

let hash(x) be the slot index computed using hash function.  
If slot hash(x) % S is full, then we try (hash(x) + 1*hash2(x)) % S
If (hash(x) + 1*hash2(x)) % S is also full, then we try (hash(x) + 2*hash2(x)) % S
If (hash(x) + 2*hash2(x)) % S is also full, then we try (hash(x) + 3*hash2(x)) % S
..................................................
..................................................

Ver esto para diagramas paso a paso. 

Comparación de los tres anteriores: 

• El sondeo lineal tiene el mejor rendimiento de caché, pero sufre de agrupamiento. Una ventaja más del sondeo lineal es fácil de calcular. 
• El sondeo cuadrático se encuentra entre los dos en términos de rendimiento de caché y agrupación. 
• El hashing doble tiene un rendimiento de caché deficiente, pero no se agrupa. El hashing doble requiere más tiempo de cálculo, ya que es necesario calcular dos funciones hash. 

S. No.	Enstringmiento separado	Direccionamiento abierto
1.	El enstringmiento es más simple de implementar.	El direccionamiento abierto requiere más cómputo.
2.	En el enstringmiento, la tabla Hash nunca se llena, siempre podemos agregar más elementos a la string.	En el direccionamiento abierto, la mesa puede llenarse.
3.	El enstringmiento es menos sensible a la función hash oa los factores de carga.	El direccionamiento abierto requiere un cuidado especial para evitar la agrupación y el factor de carga.
4.	El enstringmiento se usa principalmente cuando se desconoce cuántas claves y con qué frecuencia se pueden insertar o eliminar.	El direccionamiento abierto se utiliza cuando se conoce la frecuencia y el número de claves.
5.	El rendimiento de la memoria caché del enstringmiento no es bueno, ya que las claves se almacenan mediante una lista vinculada.	El direccionamiento abierto proporciona un mejor rendimiento de caché ya que todo se almacena en la misma tabla.
6.	Desperdicio de espacio (algunas partes de la tabla hash en el enstringmiento nunca se utilizan).	En el direccionamiento abierto, se puede usar una ranura incluso si una entrada no se asigna a ella.
7.	El enstringmiento utiliza espacio adicional para los enlaces.	No hay enlaces en el direccionamiento abierto

Nota: el rendimiento de caché del enstringmiento no es bueno porque cuando atravesamos una lista enlazada, básicamente estamos saltando de un Node a otro, en toda la memoria de la computadora. Por esta razón, la CPU no puede almacenar en caché los Nodes que aún no se han visitado, esto no nos ayuda. Pero con Open Addressing, los datos no se propagan, por lo que si la CPU detecta que se accede constantemente a un segmento de la memoria, se almacena en caché para un acceso rápido.

Rendimiento del direccionamiento abierto: 
al igual que el enstringmiento, el rendimiento del hash se puede evaluar bajo el supuesto de que cada clave tiene la misma probabilidad de ser hash en cualquier ranura de la tabla (hashing uniforme simple) 

m = Number of slots in the hash table
n = Number of keys to be inserted in the hash table
 
Load factor α = n/m  ( < 1 )

Expected time to search/insert/delete < 1/(1 - α) 

So Search, Insert and Delete take (1/(1 - α)) time