La Reina N es el problema de colocar N reinas de ajedrez en un tablero de ajedrez N × N para que no haya dos reinas que se ataquen entre sí. Por ejemplo, la siguiente es una solución para el problema de 4 Queen.
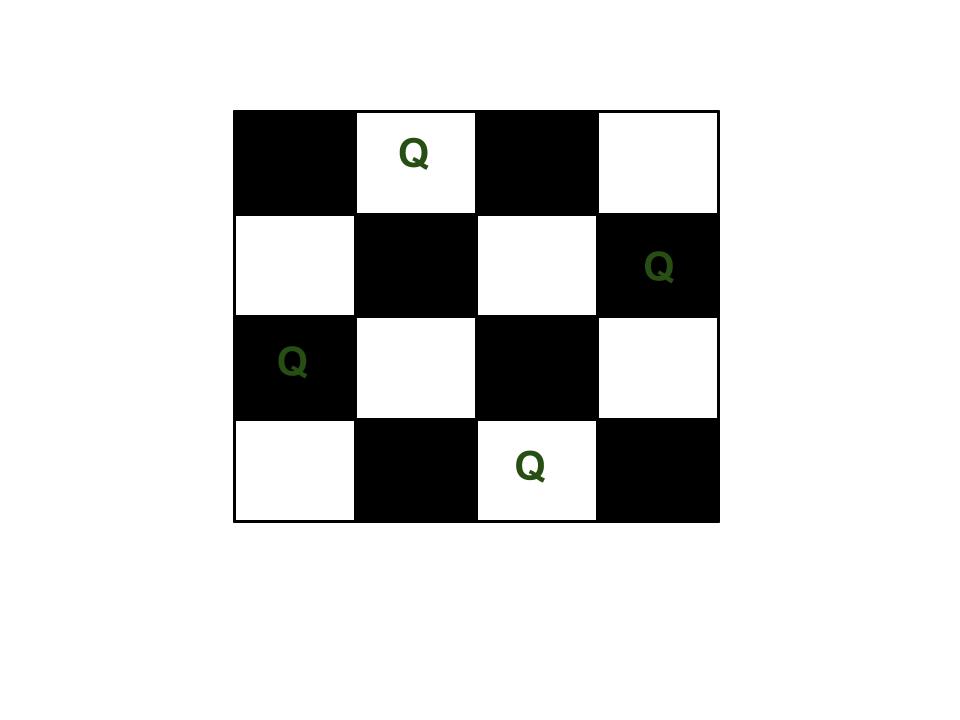
El resultado esperado es una array binaria que tiene unos para los bloques donde se colocan las reinas. Por ejemplo, la siguiente es la array de salida para la solución anterior de 4 reinas.
{ 0, 1, 0, 0}
{ 0, 0, 0, 1}
{ 1, 0, 0, 0}
{ 0, 0, 1, 0}
Python3
# Python program to solve N Queen
# Problem using backtracking
global N
N = 4
def printSolution(board):
for i in range(N):
for j in range(N):
print (board[i][j],end=' ')
print()
# A utility function to check if a queen can
# be placed on board[row][col]. Note that this
# function is called when "col" queens are
# already placed in columns from 0 to col -1.
# So we need to check only left side for
# attacking queens
def isSafe(board, row, col):
# Check this row on left side
for i in range(col):
if board[row][i] == 1:
return False
# Check upper diagonal on left side
for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
if board[i][j] == 1:
return False
# Check lower diagonal on left side
for i, j in zip(range(row, N, 1), range(col, -1, -1)):
if board[i][j] == 1:
return False
return True
def solveNQUtil(board, col):
# base case: If all queens are placed
# then return true
if col >= N:
return True
# Consider this column and try placing
# this queen in all rows one by one
for i in range(N):
if isSafe(board, i, col):
# Place this queen in board[i][col]
board[i][col] = 1
# recur to place rest of the queens
if solveNQUtil(board, col + 1) == True:
return True
# If placing queen in board[i][col
# doesn't lead to a solution, then
# queen from board[i][col]
board[i][col] = 0
# if the queen can not be placed in any row in
# this column col then return false
return False
# This function solves the N Queen problem using
# Backtracking. It mainly uses solveNQUtil() to
# solve the problem. It returns false if queens
# cannot be placed, otherwise return true and
# placement of queens in the form of 1s.
# note that there may be more than one
# solutions, this function prints one of the
# feasible solutions.
def solveNQ():
board = [ [0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]
]
if solveNQUtil(board, 0) == False:
print ("Solution does not exist")
return False
printSolution(board)
return True
# driver program to test above function
solveNQ()
# This code is contributed by Divyanshu Mehta
Producción:
0 0 1 0 1 0 0 0 0 0 0 1 0 1 0 0
Tiempo Complejidad : O(N 2 )
Espacio Auxiliar : O(N)
Consulte el artículo completo sobre el problema de N Queen | Backtracking-3 para más detalles!
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA