Finite Automata (FA) es una máquina simple que se usa para hacer coincidir patrones en una string de entrada. Finite Automata es un quíntuple, es decir, tiene cinco elementos. En este artículo vamos a ver cómo convertir epsilon-NFA a DFA usando Python y Graphviz.
El quíntuple de FA se representa como:
![]()
Los cinco elementos son:
- Un conjunto finito de Estados (Q)
- Un conjunto finito de Alfabetos de Entrada (
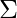 )
) - Estado de inicio (
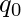 )
) - Un conjunto finito de estados finales (F)
- Función de transición (
 )
)
Los autómatas finitos (FA) son de dos tipos:
- Autómatas finitos deterministas (DFA)
- Autómatas finitos no deterministas (NFA)
Tipos de autómatas finitos:
Autómatas finitos deterministas (DFA)
Autómatas finitos deterministas (DFA) es un FA donde solo hay un estado fijo al que la máquina puede ir para un alfabeto de entrada como se define en la función de transición.
DFA no permite ![]() el alfabeto (nulo), lo que significa que la máquina no cambiará de estado si no se detecta ningún alfabeto.
el alfabeto (nulo), lo que significa que la máquina no cambiará de estado si no se detecta ningún alfabeto.
Para un DFA,
![]()
Por ejemplo, DFA acepta todas las strings formadas por f y g que contienen «gfg» como substring.

DFA
Autómatas finitos no deterministas (NFA)
Autómatas finitos no deterministas (NFA) es un FA donde la máquina puede ir a más de un estado para un alfabeto de entrada.
Para una NFA,
![]()
NFA que permite ![]() movimientos se llama E-NFA o Epsilon-NFA .
movimientos se llama E-NFA o Epsilon-NFA .
Alfabeto permitido ![]() (nulo) de NFA significa que la máquina puede cambiar de estado incluso si no se detecta ningún alfabeto de entrada.
(nulo) de NFA significa que la máquina puede cambiar de estado incluso si no se detecta ningún alfabeto de entrada.
Para un E-NFA,
![]()
Ejemplo, NFA que acepta todas las strings formadas por f y g que contienen «gfg» como substring.

NFA
La ![]() razón es que, para cada transición, hay 2 posibilidades, transitar o no transitar. Y esto es para cada estado Q. Así
razón es que, para cada transición, hay 2 posibilidades, transitar o no transitar. Y esto es para cada estado Q. Así ![]() será el total de configuraciones posibles para cada transición.
será el total de configuraciones posibles para cada transición.
¿Por qué la conversión?
Las computadoras pueden entender FA en su forma básica que está en DFA. Pero debido a las características de NFA, los humanos podemos entender NFA y mejorar E-NFA con facilidad. Entonces necesitamos convertir E-NFA a DFA.
Pasos para convertir E-NFA a DFA:
![]() – closure : It is the set of states to which we can go without any input i.e., with
– closure : It is the set of states to which we can go without any input i.e., with ![]() moves.
moves.
Paso 1: Buscar ![]() : cierre del estado de inicio de NFA y ese será el estado de inicio de DFA.
: cierre del estado de inicio de NFA y ese será el estado de inicio de DFA.
Paso 2: a partir de este conjunto, para cada alfabeto, evaluar ![]() : cierre del conjunto de transición para este alfabeto.
: cierre del conjunto de transición para este alfabeto.
Paso 3: Para cada nuevo conjunto de cierre que encontremos, repetiremos el Paso 2 hasta que no quede ningún conjunto nuevo.
Paso 4: el conjunto en DFA que contiene el estado final de NFA será el estado final del conjunto.
Por ejemplo,
Sea el E-NFA dado:

NFA
ANF: ![]()
P: {A, B, C, D}
![]() : {a, b, c}
: {a, b, c}
![]() : A
: A
F : {D}
![]() :
:
| NFA | a | b | C | |
| A | A | – | – | antes de Cristo |
| B | – | BD | – | – |
| C | – | – | CD | – |
| D | – | – | – | – |
Es un NFA para lenguaje que acepta strings del tipo: { ![]() , donde
, donde ![]() }
}
Pasos para convertir:
| estados | |
| A | A B C |
| B | B |
| C | C |
| D | D |
Paso 1: Buscar ![]() : cierre del estado de inicio de NFA y ese será el estado de inicio de DFA.
: cierre del estado de inicio de NFA y ese será el estado de inicio de DFA.
![]() – closure of start state of NFA.
– closure of start state of NFA.
![]() – closure (A) : {A,B,C}
– closure (A) : {A,B,C}
Pasos 2,3: Comenzando con este conjunto, para cada alfabeto, evaluar ![]() – cierre del conjunto de transición para este alfabeto. y Para cada nuevo conjunto de cierre que encontremos, repetiremos el paso 2 hasta que no quede ningún conjunto nuevo.
– cierre del conjunto de transición para este alfabeto. y Para cada nuevo conjunto de cierre que encontremos, repetiremos el paso 2 hasta que no quede ningún conjunto nuevo.
Conjunto actual de estados de DFA: {ABC}
- {ABC} -> a = A -> a : ABC
- {ABC} -> b = BD -> b : BD
- {ABC} -> c = CD -> c : CD
Conjunto actual de estados de DFA: {ABC, BD, CD}
- {BD} -> un =
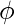
- {BD} -> b = BD
- {BD} -> c =
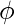
- {CD} -> un =
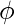
- {CD} -> b =
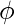
- {CD} -> c = CD
Estados de DFA, Q : {ABC, BD, CD, ![]() }
}
Función de transición ![]() :
:
| DFA | a | b | C |
| A B C | A B C | BD | CD |
| BD | BD | ||
| CD | CD | ||
Paso 4: el conjunto en DFA que contiene el estado final de NFA será el estado final del conjunto.
D fue el estado final en NFA. Entonces, todos los estados que tengan D en su conjunto serán estados finales en DFA.
Entonces, estados finales de DFA, F: {BD, CD}
DFA obtuvo:

DFA
![]() is also known as dead state because there is no outgoing edge from it. So after machine arrives in the dead state, it cannot reach the final state.
is also known as dead state because there is no outgoing edge from it. So after machine arrives in the dead state, it cannot reach the final state.
Herramientas para la implementación con código:
Graphviz: es una biblioteca de Python para visualizar diagramas gráficos.
Para instalar graphviz en python, ejecute este comando en la terminal:
pip install graphviz
Requisito previo:
Entradas :
- Número de estados: no_state
- Array de estados: estados
- Número de alfabetos: no_alphabet
- Array de alfabetos: alfabetos
- Estado de inicio: inicio
- Número de estados finales: no_final
- Array de estados finales: finales
- Número de transiciones: no_transition
- Array de transiciones: transiciones
Las transiciones son del tipo: [Desde el estado, Alfabeto, Hasta el estado]
Utilidad :
- Diccionario/Mapa para obtener el índice del estado: state_dict
- Diccionario/Mapa para obtener el índice del alfabeto: alphabets_dict
- Diccionario de tabla de transición para obtener una array de estados ‘a’ del par ‘estado’ y ‘alfabeto’: transición_tabla
- Objeto de dígrafo para almacenar el gráfico de la NFA: gráfico
Métodos/Funciones:
- Constructor de la clase NFA: __init__()
Inicializa todas las variables de entrada y evalúa los valores de las variables de utilidad de entrada. - Obtener información del usuario: método de clase fromUser()
para obtener información del usuario. - Representación del quíntuple de NFA: __repr__()
- Encuentre el cierre de épsilon de un estado: getEpsilonClosure(state)
Para encontrar el cierre de épsilon de un estado, mantenemos una pila para obtener qué estado evaluar a continuación y un diccionario para rastrear qué estados han sido evaluados.
Comenzamos un bucle while desde el estado inicial y encontramos sus estados de transición épsilon.
Empujamos todos estos estados a la pila (stack.push(stata)) y los marcamos en el diccionario (dict[state]=0).
También marcamos este estado como completo en el diccionario (dict[state]=1).
Para cada iteración siguiente, sacamos la parte superior de la pila cada vez y la evaluamos si no se evalúa consultando el diccionario. - Encuentre el nombre de estado apropiado para el diagrama de DFA convertido a partir de una array de estados: getStateName(state_list)
Como obtendremos una lista de estados de la evaluación, para mostrar en el diagrama de DFA, necesitamos un nombre propio que será la concatenación de todos los nombres en el conjunto.
Por ejemplo: para indicar que el conjunto es ={A,B,D}, esta función devolverá una string = «ABD». - Verifique si la array contiene un estado final de NFA para encontrar si la array será el estado final en DFA: isFinalDFA(state_list)
Esta función verifica si una lista de estados contiene un estado que es un estado final en NFA, que a su vez indicará si el conjunto es definitivo o no.
Por ejemplo: el conjunto que estamos comprobando es = {A,B,D}, y D es un estado final en NFA. Entonces esta función devolverá True para este conjunto de entrada. Por lo tanto, este conjunto será el estado final en DFA.
Acercarse:
- Cree un objeto de la clase NFA: nfa e inicialícelo con valores predefinidos usando un constructor o usando la entrada del usuario.
- Inicialice el nfa.graph con Nodes y bordes de acuerdo con los valores de entrada.
- Muestre/Represente el gráfico NFA.
- Cree otro objeto Digraph para almacenar valores del DFA obtenido y representar el diagrama: dfa .
- Evalúe el cierre épsilon de todos los estados de NFA para no volver a calcular cada vez y guárdelo en el diccionario con un par clave-valor como [estado -> lista de estados de cierre]: epsilon_closure{}
- Cree una pila para rastrear qué estado de DFA evaluar a continuación: dfa_stack[]
- Agregue el cierre épsilon del estado de inicio de NFA como el estado de inicio de DFA.
- Haga una lista para mantener todos los estados presentes en el DFA: dfa_states[]
- Inicie un ciclo while que continuamos hasta que no haya nuevos estados en dfa_stack.
- Abrimos la parte superior de dfa_stack para evaluar el conjunto actual de estados: cur_state.
- Recorremos todos los alfabetos para el conjunto actual de estados.
- Creamos un conjunto para mantener el cierre épsilon de todos los estados en el conjunto actual: from_closure{}
- Si este conjunto no está vacío,
- Hacemos otro conjunto para mantener el conjunto to_state .
- Si este conjunto no está presente en dfa_states , lo agregamos en dfa_stack y dfa_states.
- Luego agregamos este Node en el gráfico dfa y agregamos un borde entre cur_state y to_state.
- De lo contrario, este conjunto está vacío, entonces
- Este caso es para estado muerto.
- Si el estado inactivo no está presente en dfa , agregamos el nuevo estado
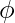 . Y hacemos todas las transiciones de todos los alfabetos a sí mismo para que la máquina nunca pueda salir del estado muerto.
. Y hacemos todas las transiciones de todos los alfabetos a sí mismo para que la máquina nunca pueda salir del estado muerto. - Hacemos la transición de cur_state a este dead_state.
- Por fin, todos los estados han sido evaluados. Así que representaremos/veremos este gráfico dfa .
A continuación se muestra la implementación completa:
Python3
# Conversion of epsilon-NFA to DFA and visualization using Graphviz
from graphviz import Digraph
class NFA:
def __init__(self, no_state, states, no_alphabet, alphabets, start,
no_final, finals, no_transition, transitions):
self.no_state = no_state
self.states = states
self.no_alphabet = no_alphabet
self.alphabets = alphabets
# Adding epsilon alphabet to the list
# and incrementing the alphabet count
self.alphabets.append('e')
self.no_alphabet += 1
self.start = start
self.no_final = no_final
self.finals = finals
self.no_transition = no_transition
self.transitions = transitions
self.graph = Digraph()
# Dictionaries to get index of states or alphabets
self.states_dict = dict()
for i in range(self.no_state):
self.states_dict[self.states[i]] = i
self.alphabets_dict = dict()
for i in range(self.no_alphabet):
self.alphabets_dict[self.alphabets[i]] = i
# transition table is of the form
# [From State + Alphabet pair] -> [Set of To States]
self.transition_table = dict()
for i in range(self.no_state):
for j in range(self.no_alphabet):
self.transition_table[str(i)+str(j)] = []
for i in range(self.no_transition):
self.transition_table[str(self.states_dict[self.transitions[i][0]])
+ str(self.alphabets_dict[
self.transitions[i][1]])].append(
self.states_dict[self.transitions[i][2]])
# Method to get input from User
@classmethod
def fromUser(cls):
no_state = int(input("Number of States : "))
states = list(input("States : ").split())
no_alphabet = int(input("Number of Alphabets : "))
alphabets = list(input("Alphabets : ").split())
start = input("Start State : ")
no_final = int(input("Number of Final States : "))
finals = list(input("Final States : ").split())
no_transition = int(input("Number of Transitions : "))
transitions = list()
print("Enter Transitions (from alphabet to) (e for epsilon): ")
for i in range(no_transition):
transitions.append(input("-> ").split())
return cls(no_state, states, no_alphabet, alphabets, start,
no_final, finals, no_transition, transitions)
# Method to represent quintuple
def __repr__(self):
return "Q : " + str(self.states)+"\nΣ : "
+ str(self.alphabets)+"\nq0 : "
+ str(self.start)+"\nF : "+str(self.finals) + \
"\nδ : \n" + str(self.transition_table)
def getEpsilonClosure(self, state):
# Method to get Epsilon Closure of a state of NFA
# Make a dictionary to track if the state has been visited before
# And a array that will act as a stack to get the state to visit next
closure = dict()
closure[self.states_dict[state]] = 0
closure_stack = [self.states_dict[state]]
# While stack is not empty the loop will run
while (len(closure_stack) > 0):
# Get the top of stack that will be evaluated now
cur = closure_stack.pop(0)
# For the epsilon transition of that state,
# if not present in closure array then add to dict and push to stack
for x in self.transition_table[
str(cur)+str(self.alphabets_dict['e'])]:
if x not in closure.keys():
closure[x] = 0
closure_stack.append(x)
closure[cur] = 1
return closure.keys()
def getStateName(self, state_list):
# Get name from set of states to display in the final DFA diagram
name = ''
for x in state_list:
name += self.states[x]
return name
def isFinalDFA(self, state_list):
# Method to check if the set of state is final state in DFA
# by checking if any of the set is a final state in NFA
for x in state_list:
for y in self.finals:
if (x == self.states_dict[y]):
return True
return False
print("E-NFA to DFA")
# INPUT
# Number of States : no_state
# Array of States : states
# Number of Alphabets : no_alphabet
# Array of Alphabets : alphabets
# Start State : start
# Number of Final States : no_final
# Array of Final States : finals
# Number of Transitions : no_transition
# Array of Transitions : transitions
nfa = NFA(
4, # number of states
['A', 'B', 'C', 'D'], # array of states
3, # number of alphabets
['a', 'b', 'c'], # array of alphabets
'A', # start state
1, # number of final states
['D'], # array of final states
7, # number of transitions
[['A', 'a', 'A'], ['A', 'e', 'B'], ['B', 'b', 'B'],
['A', 'e', 'C'], ['C', 'c', 'C'], ['B', 'b', 'D'],
['C', 'c', 'D']]
# array of transitions with its element of type :
# [from state, alphabet, to state]
)
# nfa = NFA.fromUser() # To get input from user
# print(repr(nfa)) # To print the quintuple in console
# Making an object of Digraph to visualize NFA diagram
nfa.graph = Digraph()
# Adding states/nodes in NFA diagram
for x in nfa.states:
# If state is not a final state, then border shape is single circle
# Else it is double circle
if (x not in nfa.finals):
nfa.graph.attr('node', shape='circle')
nfa.graph.node(x)
else:
nfa.graph.attr('node', shape='doublecircle')
nfa.graph.node(x)
# Adding start state arrow in NFA diagram
nfa.graph.attr('node', shape='none')
nfa.graph.node('')
nfa.graph.edge('', nfa.start)
# Adding edge between states in NFA from the transitions array
for x in nfa.transitions:
nfa.graph.edge(x[0], x[2], label=('ε', x[1])[x[1] != 'e'])
# Makes a pdf with name nfa.graph.pdf and views the pdf
nfa.graph.render('nfa', view=True)
# Making an object of Digraph to visualize DFA diagram
dfa = Digraph()
# Finding epsilon closure beforehand so to not recalculate each time
epsilon_closure = dict()
for x in nfa.states:
epsilon_closure[x] = list(nfa.getEpsilonClosure(x))
# First state of DFA will be epsilon closure of start state of NFA
# This list will act as stack to maintain till when to evaluate the states
dfa_stack = list()
dfa_stack.append(epsilon_closure[nfa.start])
# Check if start state is the final state in DFA
if (nfa.isFinalDFA(dfa_stack[0])):
dfa.attr('node', shape='doublecircle')
else:
dfa.attr('node', shape='circle')
dfa.node(nfa.getStateName(dfa_stack[0]))
# Adding start state arrow to start state in DFA
dfa.attr('node', shape='none')
dfa.node('')
dfa.edge('', nfa.getStateName(dfa_stack[0]))
# List to store the states of DFA
dfa_states = list()
dfa_states.append(epsilon_closure[nfa.start])
# Loop will run till this stack is not empty
while (len(dfa_stack) > 0):
# Getting top of the stack for current evaluation
cur_state = dfa_stack.pop(0)
# Traversing through all the alphabets for evaluating transitions in DFA
for al in range((nfa.no_alphabet) - 1):
# Set to see if the epsilon closure of the set is empty or not
from_closure = set()
for x in cur_state:
# Performing Union update and adding all the new states in set
from_closure.update(
set(nfa.transition_table[str(x)+str(al)]))
# Check if epsilon closure of the new set is not empty
if (len(from_closure) > 0):
# Set for the To state set in DFA
to_state = set()
for x in list(from_closure):
to_state.update(set(epsilon_closure[nfa.states[x]]))
# Check if the to state already exists in DFA and if not then add it
if list(to_state) not in dfa_states:
dfa_stack.append(list(to_state))
dfa_states.append(list(to_state))
# Check if this set contains final state of NFA
# to get if this set will be final state in DFA
if (nfa.isFinalDFA(list(to_state))):
dfa.attr('node', shape='doublecircle')
else:
dfa.attr('node', shape='circle')
dfa.node(nfa.getStateName(list(to_state)))
# Adding edge between from state and to state
dfa.edge(nfa.getStateName(cur_state),
nfa.getStateName(list(to_state)),
label=nfa.alphabets[al])
# Else case for empty epsilon closure
# This is a dead state(ϕ) in DFA
else:
# Check if any dead state was present before this
# if not then make a new dead state ϕ
if (-1) not in dfa_states:
dfa.attr('node', shape='circle')
dfa.node('ϕ')
# For new dead state, add all transitions to itself,
# so that machine cannot leave the dead state
for alpha in range(nfa.no_alphabet - 1):
dfa.edge('ϕ', 'ϕ', nfa.alphabets[alpha])
# Adding -1 to list to mark that dead state is present
dfa_states.append(-1)
# Adding transition to dead state
dfa.edge(nfa.getStateName(cur_state,),
'ϕ', label = nfa.alphabets[al])
# Makes a pdf with name dfa.pdf and views the pdf
dfa.render('dfa', view = True)
Producción:

DFA
La complejidad del algoritmo para convertir NFA a DFA:
Complejidad del tiempo: ![]()
Complejidad espacial: ![]()
Donde, Q = No. de Estados de NFA, N = No. de Alfabetos de NFA.
Publicación traducida automáticamente
Artículo escrito por vasugondaliya y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA