Dada una array y la tarea es verificar que la array sea array involutiva o no.
Array involutiva : Se dice que una array es array involutiva si la array multiplicada por sí misma devuelve la array identidad. La array involutiva es la array que es su propia inversa. Se dice que la array A es array involutiva si A * A = I . Donde I es la array identidad.
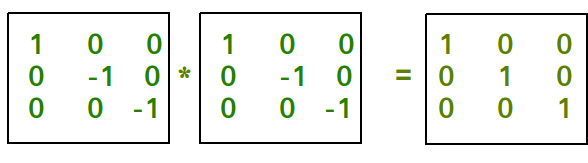
Ejemplos:
Input : mat[N][N] = {{1, 0, 0},
{0, -1, 0},
{0, 0, -1}}
Output : Involutory Matrix
Input : mat[N][N] = {{1, 0, 0},
{0, 1, 0},
{0, 0, 1}}
Output : Involutory Matrix
PHP
<?php
// Program to implement
// involutory matrix.
$N = 3;
// Function for matrix
// multiplication.
function multiply($mat, $res)
{
global $N;
for ($i = 0; $i < $N; $i++)
{
for ($j = 0; $j < $N; $j++)
{
$res[$i][$j] = 0;
for ($k = 0; $k < $N; $k++)
$res[$i][$j] += $mat[$i][$k] *
$mat[$k][$j];
}
}
return $res;
}
// Function to check
// involutory matrix.
function InvolutoryMatrix($mat)
{
global $N;
$res;
for ($i = 0; $i < $N; $i++)
for ($j = 0; $j < $N; $j++)
$res[$i][$j] = 0;
// multiply function call.
$res = multiply($mat, $res);
for ($i = 0; $i < $N; $i++)
{
for ($j = 0; $j < $N; $j++)
{
if ($i == $j &&
$res[$i][$j] != 1)
return false;
if ($i != $j &&
$res[$i][$j] != 0)
return false;
}
}
return true;
}
// Driver Code
$mat = array(array(1, 0, 0),
array(0, -1, 0),
array(0, 0, -1));
// Function call. If function
// return true then if part
// will execute otherwise
// else part will execute.
if (InvolutoryMatrix($mat))
echo "Involutory Matrix";
else
echo "Not Involutory Matrix";
// This code is contributed by mits
?>
Producción :
Involutory Matrix
¡ Consulte el artículo completo sobre el Programa para consultar la Array involuntaria para obtener más detalles!
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA