La medición se ocupa de las cantidades pertenecientes a varias formas geométricas y su medida. Se puede clasificar en dos tipos: medición 2D y medición 3D. Como sugieren los nombres, el primero se ocupa de aquellas formas que tienen solo dos dimensiones: largo y ancho; mientras que el segundo se ocupa de aquellas formas que tienen tres dimensiones: largo, ancho y alto.
Trapecio isósceles
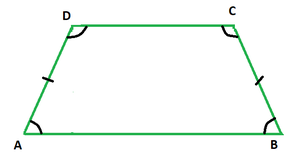
Un trapecio isósceles es un cuadrilátero que tiene exactamente un par de lados paralelos y el otro par no es paralelo y tiene la misma longitud. Como cualquier otro cuadrilátero, la suma de sus ángulos siempre mide 360°. La siguiente figura representa un trapecio isósceles ABCD, donde AB ∥ CD y los lados no paralelos tienen la misma longitud, es decir, AD = BC.
Área de un trapecio
El área de un trapecio es la mitad del producto de la suma de sus lados paralelos por la distancia entre dichos lados paralelos, es decir, la altura o altura del trapecio.
A = ½ × (a + b) × h
dónde,
a y b representan las longitudes de los lados paralelos y h es la altura del trapecio.
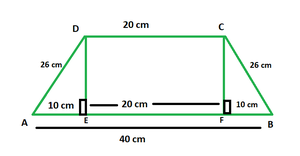
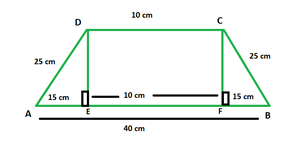
Calcula el área del trapecio si la longitud de los lados paralelos es de 40 cm y 20 cm y los lados no paralelos son iguales y tienen una longitud de 26 cm.
Solución:
Área de un trapecio = ½ × (a + b) × h …(i)
En la figura de arriba, DCEF es un rectángulo con l = 20 cm. △ADE y △CFB son triángulos rectángulos con hipotenusa de 26 cm y base de 10 cm cada uno.
En △ADE derecho, usando el Teorema de Pitágoras, tenemos:
AD 2 = AE 2 + DE 2
⇒ 26 2 − 10 2 = DE 2
⇒ DE = 24 cm
Así, altura del trapecio = h = 24 cm, a = 20 cm yb = 40 cm.
Sustituyendo los valores anteriores en la ec. (yo), tenemos:
A = ½ × (20 + 40) × 24
Área del trapecio = 720 cm2.
Problemas similares
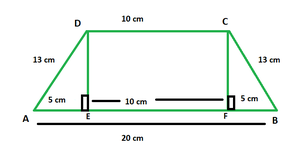
Pregunta 1. En un trapecio, los lados paralelos miden 20 cm y 10 cm. Calcula el área del trapecio si sus lados no paralelos son iguales y tienen una longitud de 13 cm.
Solución:
Área de un trapecio = ½ × (a + b) × h …(i)
En la figura de arriba, DCEF es un rectángulo con l = 10 cm. △ADE y △CFB son triángulos rectángulos con hipotenusa de 13 cm y base de 5 cm cada uno.
En △ADE derecho, usando el Teorema de Pitágoras, tenemos:
AD 2 = AE 2 + DE 2
⇒ 13 2 − 5 2 = DE 2
⇒ DE = 12 cm
Así, altura del trapecio = h = 12 cm, a = 10 cm yb = 20 cm.
Sustituyendo los valores anteriores en la ec. (yo), tenemos:
A = ½ × (10 + 20) × 12
Área del trapecio = 180 cm2.
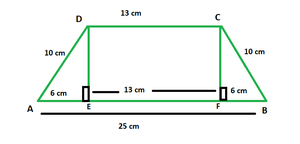
Pregunta 2. En un trapecio, los lados paralelos miden 13 cm y 25 cm. Calcula el área del trapecio si sus lados no paralelos son iguales y tienen una longitud de 10 cm.
Solución:
Área de un trapecio = ½ × (a + b) × h …(i)
En la figura de arriba, DCEF es un rectángulo con l = 13 cm. △ADE y △CFB son triángulos rectángulos con hipotenusa de 10 cm y base de 6 cm cada uno.
En △ADE derecho, usando el Teorema de Pitágoras, tenemos:
AD2 = AE 2 + DE 2
⇒ 10 2 − 6 2 = DE 2
⇒ DE = 8 cm
Así, altura del trapecio = h = 8 cm, a = 13 cm yb = 25 cm.
Sustituyendo los valores anteriores en la ec. (yo), tenemos:
A = ½ × (13 + 25) × 8
Área del trapecio = 152 cm2.
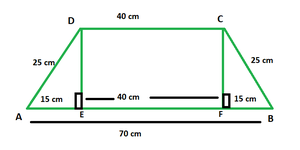
Pregunta 3. En un trapecio, los lados paralelos miden 40 cm y 70 cm. Calcula el área del trapecio si sus lados no paralelos son iguales y tienen longitudes de 25 cm.
Solución:
Área de un trapecio = ½ × (a + b) × h …(i)
En la figura de arriba, DCEF es un rectángulo con l = 40 cm. △ADE y △CFB son triángulos rectángulos con hipotenusa de 25 cm y base de 15 cm cada uno.
En △ADE derecho, usando el Teorema de Pitágoras, tenemos:
AD 2 = AE 2 + DE 2
⇒ 25 2 − 15 2 = DE 2
⇒ DE = 20 cm
Así, altura del trapecio = h = 20 cm, a = 40 cm yb = 70 cm.
Sustituyendo los valores anteriores en la ec. (yo), tenemos:
A = ½ × (40 + 70) × 20
Área del trapecio = 1100 cm2.
Pregunta 4. En un trapecio, los lados paralelos miden 40 cm y 10 cm. Calcula el área del trapecio si sus lados no paralelos son iguales y tienen longitudes de 25 cm.
Solución:
Área de un trapecio = ½ × (a + b) × h …(i)
En la figura de arriba, DCEF es un rectángulo con l = 13 cm. △ADE y △CFB son triángulos rectángulos con hipotenusa de 10 cm y base de 6 cm cada uno.
En △ADE derecho, usando el Teorema de Pitágoras, tenemos:
AD 2 = AE 2 + DE 2
⇒ 25 2 − 15 2 = DE 2
⇒ DE = 20 cm
Así, altura del trapecio = h = 20 cm, a = 10 cm yb = 40 cm.
Sustituyendo los valores anteriores en la ec. (yo), tenemos:
A = ½ × (10 + 40) × 20
Área del trapecio = 500 cm2.
Publicación traducida automáticamente
Artículo escrito por parmarraman44 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA