En álgebra lineal, el polinomio característico de una array cuadrada es un polinomio que es invariante bajo similitud de arrays y tiene los valores propios como raíces. Tiene el determinante y la traza de la array entre sus coeficientes.
El polinomio característico de la array 3×3 se puede calcular mediante la fórmula
x 3 – (Rastro de array)*x 2 + (Suma de menores a lo largo de la diagonal)*x – determinante de array = 0
Ejemplo:
Entrada: mat[][] = { { 0, 1, 2 }, { 1, 0, -1 }, { 2, -1, 0 } }
Salida: x^3 – 6x + 4
Enfoque : dividamos la fórmula y encontremos el valor de cada término uno por uno:
Rastro de la array
Traza de una Array la suma de los elementos a lo largo de su diagonal.
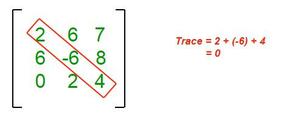
Rastro de Matrix
Menor de la array
-
- El menor de la array es para cada elemento de la array y es igual a la parte de la array que queda después de excluir la fila y la columna que contiene ese elemento en particular. La nueva array formada con los menores de cada elemento de la array dada se llama menor de la array.
- Cada nuevo elemento de la array menor se puede lograr de la siguiente manera:
-
- El determinante de una array es un número especial que se define solo para arrays cuadradas (arrays que tienen el mismo número de filas y columnas). El determinante se usa en muchos lugares en cálculo y otro álgebra relacionada con arrays, en realidad representa la array en términos de un número real que se puede usar para resolver un sistema de ecuaciones lineales y encontrar la inversa de una array.
Programa para hallar Polinomio Característico de una Array Cuadrada
C++
// C++ code to calculate
// characteristic polynomial of 3x3 matrix
#include <bits/stdc++.h>
using namespace std;
#define N 3
// Trace
int findTrace(int mat[N][N], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += mat[i][i];
return sum;
}
// Sum of minors along diagonal
int sum_of_minors(int mat[N][N], int n)
{
return (
(mat[2][2] * mat[1][1] - mat[2][1] * mat[1][2])
+ (mat[2][2] * mat[0][0] - mat[2][0] * mat[0][2])
+ (mat[1][1] * mat[0][0] - mat[1][0] * mat[0][1]));
}
// Function to get cofactor of mat[p][q]
// in temp[][]. n is current dimension of mat[][]
// Cofactor will be used for calculating determinant
void getCofactor(int mat[N][N], int temp[N][N], int p,
int q, int n)
{
int i = 0, j = 0;
// Looping for each element of the matrix
for (int row = 0; row < n; row++) {
for (int col = 0; col < n; col++) {
// Copying into temporary matrix only those
// element which are not in given row and
// column
if (row != p && col != q) {
temp[i][j++] = mat[row][col];
// Row is filled, so increase row index
// and reset col index
if (j == n - 1) {
j = 0;
i++;
}
}
}
}
}
// Function for calculating
// determinant of matrix
int determinantOfMatrix(int mat[N][N], int n)
{
// Initialize result
int D = 0;
// Base case : if matrix
// contains single element
if (n == 1)
return mat[0][0];
// To store cofactors
int temp[N][N];
// To store sign multiplier
int sign = 1;
// Iterate for each element of first row
for (int f = 0; f < n; f++) {
// Getting Cofactor of mat[0][f]
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0][f]
* determinantOfMatrix(temp, n - 1);
// Terms are to be added with alternate sign
sign = -sign;
}
return D;
}
// Driver Code
int main()
{
// Given matrix
int mat[N][N]
= { { 0, 1, 2 }, { 1, 0, -1 }, { 2, -1, 0 } };
int trace = findTrace(mat, 3);
int s_o_m = sum_of_minors(mat, 3);
int det = determinantOfMatrix(mat, 3);
cout << "x^3";
if (trace != 0) {
trace < 0 ? cout << " + " << trace * -1 << "x^2"
: cout << " - " << trace << "x^2";
}
if (s_o_m != 0) {
s_o_m < 0 ? cout << " - " << s_o_m * -1 << "x"
: cout << " + " << s_o_m << "x";
}
if (det != 0) {
det < 0 ? cout << " + " << det * -1
: cout << " - " << det;
}
return 0;
}
Java
// Java code to calculate
// characteristic polynomial of 3x3 matrix
import java.util.*;
class GFG{
static final int N =3;
// Trace
static int findTrace(int mat[][], int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += mat[i][i];
return sum;
}
// Sum of minors along diagonal
static int sum_of_minors(int mat[][], int n)
{
return (
(mat[2][2] * mat[1][1] - mat[2][1] * mat[1][2])
+ (mat[2][2] * mat[0][0] - mat[2][0] * mat[0][2])
+ (mat[1][1] * mat[0][0] - mat[1][0] * mat[0][1]));
}
// Function to get cofactor of mat[p][q]
// in temp[][]. n is current dimension of mat[][]
// Cofactor will be used for calculating determinant
static void getCofactor(int mat[][], int temp[][], int p,
int q, int n)
{
int i = 0, j = 0;
// Looping for each element of the matrix
for (int row = 0; row < n; row++) {
for (int col = 0; col < n; col++) {
// Copying into temporary matrix only those
// element which are not in given row and
// column
if (row != p && col != q) {
temp[i][j++] = mat[row][col];
// Row is filled, so increase row index
// and reset col index
if (j == n - 1) {
j = 0;
i++;
}
}
}
}
}
// Function for calculating
// determinant of matrix
static int determinantOfMatrix(int mat[][], int n)
{
// Initialize result
int D = 0;
// Base case : if matrix
// contains single element
if (n == 1)
return mat[0][0];
// To store cofactors
int [][]temp = new int[N][N];
// To store sign multiplier
int sign = 1;
// Iterate for each element of first row
for (int f = 0; f < n; f++) {
// Getting Cofactor of mat[0][f]
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0][f]
* determinantOfMatrix(temp, n - 1);
// Terms are to be added with alternate sign
sign = -sign;
}
return D;
}
// Driver Code
public static void main(String[] args)
{
// Given matrix
int [][]mat
= { { 0, 1, 2 }, { 1, 0, -1 }, { 2, -1, 0 } };
int trace = findTrace(mat, 3);
int s_o_m = sum_of_minors(mat, 3);
int det = determinantOfMatrix(mat, 3);
System.out.print("x^3");
if (trace != 0) {
if(trace < 0)
System.out.print(" + " + trace * -1+ "x^2");
else
System.out.print(" - " + trace+ "x^2");
}
if (s_o_m != 0) {
if(s_o_m < 0 )
System.out.print(" - " + s_o_m * -1+ "x");
else
System.out.print(" + " + s_o_m+ "x");
}
if (det != 0) {
if(det < 0 )
System.out.print(" + " + det * -1);
else
System.out.print(" - " + det);
}
}
}
// This code is contributed by Rajput-Ji
Python3
# JavaScript code for the above approach
N = 3
# Trace
def findTrace(mat, n):
sum = 0
for i in range(n):
sum += mat[i][i]
return sum
# Sum of minors along diagonal
def sum_of_minors(mat, n):
return ((mat[2][2] * mat[1][1] - mat[2][1] * mat[1][2])
+ (mat[2][2] * mat[0][0] - mat[2][0] * mat[0][2])
+ (mat[1][1] * mat[0][0] - mat[1][0] * mat[0][1]))
# Function to get cofactor of mat[p][q]
# in temp[][]. n is current dimension of mat[][]
# Cofactor will be used for calculating determinant
def getCofactor(mat, temp, p, q, n):
i,j = 0,0
# Looping for each element of the matrix
for row in range(n):
for col in range(n):
# Copying into temporary matrix only those
# element which are not in given row and
# column
if (row != p and col != q):
temp[i][j] = mat[row][col]
j += 1
# Row is filled, so increase row index
# and reset col index
if (j == n - 1):
j = 0
i += 1
# Function for calculating
# determinant of matrix
def determinantOfMatrix(mat, n):
# Initialize result
D = 0
# Base case : if matrix
# contains single element
if (n == 1):
return mat[0][0]
# To store cofactors
temp = [[0 for i in range(n)] for j in range(n)]
# To store sign multiplier
sign = 1
# Iterate for each element of first row
for f in range(n):
# Getting Cofactor of mat[0][f]
getCofactor(mat, temp, 0, f, n)
D += sign * mat[0][f] * determinantOfMatrix(temp, n - 1)
# Terms are to be added with alternate sign
sign = -sign
return D
# Driver Code
# Given matrix
mat = [[0, 1, 2], [1, 0, -1], [2, -1, 0]]
trace = findTrace(mat, 3)
s_o_m = sum_of_minors(mat, 3)
det = determinantOfMatrix(mat, 3)
print("x^3",end="")
if (trace != 0):
print(f" {trace * -1}x^2",end="") if(trace < 0) else print(f" - {trace}x^2",end="")
if (s_o_m != 0):
print(f" - {s_o_m * -1}x",end="") if(s_o_m < 0) else print(f" + {s_o_m}x",end="")
if (det != 0):
print(f" + {det * -1}",end="") if (det < 0) else print(f" - {det}",end="")
# This code is contributed by shinjanpatra
C#
// C# code to calculate
// characteristic polynomial of 3x3 matrix
using System;
class GFG {
static int N = 3;
// Trace
static int findTrace(int[, ] mat, int n)
{
int sum = 0;
for (int i = 0; i < n; i++)
sum += mat[i, i];
return sum;
}
// Sum of minors along diagonal
static int sum_of_minors(int[, ] mat, int n)
{
return (
(mat[2, 2] * mat[1, 1] - mat[2, 1] * mat[1, 2])
+ (mat[2, 2] * mat[0, 0]
- mat[2, 0] * mat[0, 2])
+ (mat[1, 1] * mat[0, 0]
- mat[1, 0] * mat[0, 1]));
}
// Function to get cofactor of mat[p][q]
// in temp[][]. n is current dimension of mat[][]
// Cofactor will be used for calculating determinant
static void getCofactor(int[, ] mat, int[, ] temp,
int p, int q, int n)
{
int i = 0, j = 0;
// Looping for each element of the matrix
for (int row = 0; row < n; row++) {
for (int col = 0; col < n; col++) {
// Copying into temporary matrix only those
// element which are not in given row and
// column
if (row != p && col != q) {
temp[i, j++] = mat[row, col];
// Row is filled, so increase row index
// and reset col index
if (j == n - 1) {
j = 0;
i++;
}
}
}
}
}
// Function for calculating
// determinant of matrix
static int determinantOfMatrix(int[, ] mat, int n)
{
// Initialize result
int D = 0;
// Base case : if matrix
// contains single element
if (n == 1)
return mat[0, 0];
// To store cofactors
int[, ] temp = new int[N, N];
// To store sign multiplier
int sign = 1;
// Iterate for each element of first row
for (int f = 0; f < n; f++) {
// Getting Cofactor of mat[0][f]
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0, f]
* determinantOfMatrix(temp, n - 1);
// Terms are to be added with alternate sign
sign = -sign;
}
return D;
}
// Driver Code
public static void Main()
{
// Given matrix
int[, ] mat
= { { 0, 1, 2 }, { 1, 0, -1 }, { 2, -1, 0 } };
int trace = findTrace(mat, 3);
int s_o_m = sum_of_minors(mat, 3);
int det = determinantOfMatrix(mat, 3);
Console.Write("x^3");
if (trace != 0) {
if (trace < 0)
Console.Write(" + " + trace * -1 + "x^2");
else
Console.Write(" - " + trace + "x^2");
}
if (s_o_m != 0) {
if (s_o_m < 0)
Console.Write(" - " + s_o_m * -1 + "x");
else
Console.Write(" + " + s_o_m + "x");
}
if (det != 0) {
if (det < 0)
Console.Write(" + " + det * -1);
else
Console.Write(" - " + det);
}
}
}
// This code is contributed by ukasp.
Javascript
<script>
// JavaScript code for the above approach
let N = 3
// Trace
function findTrace(mat, n) {
let sum = 0;
for (let i = 0; i < n; i++)
sum += mat[i][i];
return sum;
}
// Sum of minors along diagonal
function sum_of_minors(mat, n) {
return (
(mat[2][2] * mat[1][1] - mat[2][1] * mat[1][2])
+ (mat[2][2] * mat[0][0] - mat[2][0] * mat[0][2])
+ (mat[1][1] * mat[0][0] - mat[1][0] * mat[0][1]));
}
// Function to get cofactor of mat[p][q]
// in temp[][]. n is current dimension of mat[][]
// Cofactor will be used for calculating determinant
function getCofactor(mat, temp, p,
q, n) {
let i = 0, j = 0;
// Looping for each element of the matrix
for (let row = 0; row < n; row++) {
for (let col = 0; col < n; col++) {
// Copying into temporary matrix only those
// element which are not in given row and
// column
if (row != p && col != q) {
temp[i][j++] = mat[row][col];
// Row is filled, so increase row index
// and reset col index
if (j == n - 1) {
j = 0;
i++;
}
}
}
}
}
// Function for calculating
// determinant of matrix
function determinantOfMatrix(mat, n) {
// Initialize result
let D = 0;
// Base case : if matrix
// contains single element
if (n == 1)
return mat[0][0];
// To store cofactors
let temp = new Array(n)
for (let i = 0; i < temp.length; i++) {
temp[i] = new Array(n)
}
// To store sign multiplier
let sign = 1;
// Iterate for each element of first row
for (let f = 0; f < n; f++) {
// Getting Cofactor of mat[0][f]
getCofactor(mat, temp, 0, f, n);
D += sign * mat[0][f]
* determinantOfMatrix(temp, n - 1);
// Terms are to be added with alternate sign
sign = -sign;
}
return D;
}
// Driver Code
// Given matrix
let mat
= [[0, 1, 2], [1, 0, -1], [2, -1, 0]];
let trace = findTrace(mat, 3);
let s_o_m = sum_of_minors(mat, 3);
let det = determinantOfMatrix(mat, 3);
document.write("x^3");
if (trace != 0) {
trace < 0 ? document.write(" + " + trace * -1 + "x^2")
: document.write(" - " + trace + "x^2");
}
if (s_o_m != 0) {
s_o_m < 0 ? document.write(" - " + s_o_m * -1 + "x")
: document.write(" + " + s_o_m + "x");
}
if (det != 0) {
det < 0 ? document.write(" + " + det * -1)
: document.write(" - " + det);
}
// This code is contributed by Potta Lokesh
</script>
x^3 - 6x + 4
Complejidad temporal: O(N 3 ), donde N es el tamaño de una array cuadrada
Espacio auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por jainuditkumar y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA