Matemáticas | Conjunto de Distribuciones de Probabilidad 1 (Distribución Uniforme)

Requisito previo: variable aleatoria

En la teoría de la probabilidad y la estadística, una distribución de probabilidad es una función matemática que se puede considerar que proporciona las probabilidades de ocurrencia de diferentes resultados posibles en un experimento. Por ejemplo, si la variable aleatoria $X$ se usa para denotar el resultado de un lanzamiento de una moneda («el experimento»), entonces la distribución de probabilidad de $X$ tomaría el valor de 0.5 para $X$ = cara y 0.5 para $X$ = cruz (suponiendo que la moneda es justa) .
Las distribuciones de probabilidad se dividen en dos clases:

Distribución de probabilidad discreta: si las probabilidades se definen en una variable aleatoria discreta, que solo puede tomar un conjunto discreto de valores, entonces se dice que la distribución es una distribución de probabilidad discreta. Por ejemplo, el evento de lanzar un dado se puede representar mediante una variable aleatoria discreta con una distribución de probabilidad tal que cada evento tenga una probabilidad de $\:\frac{1}{6}$ .
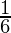Distribución de probabilidad continua: si las probabilidades se definen en una variable aleatoria continua, que puede tomar cualquier valor entre dos números, se dice que la distribución es una distribución de probabilidad continua. Por ejemplo, la temperatura a lo largo de un día determinado se puede representar mediante una variable aleatoria continua y se dice que la distribución de probabilidad correspondiente es continua.

Función de distribución acumulativa:
similar a la función de densidad de probabilidad, la función de distribución acumulativa $F(x)$ de una variable aleatoria X de valor real, o simplemente la función de distribución $X$ evaluada en $x$ , es la probabilidad que $X$ tomará un valor menor o igual que $x$ .
Para una variable aleatoria discreta,
$F(x) = P(X\leq x) = \sum \limits_{x_0\leq x} P(x_0)$
para una variable aleatoria continua,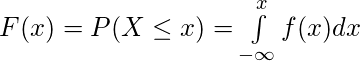
$F(x) = P(X\leq x) = \int \limits_{-\infty}^{x} f(x)dx$

Distribución de probabilidad uniforme –

La Distribución Uniforme, también conocida como Distribución Rectangular , es un tipo de Distribución de Probabilidad Continua.
Tiene una Variable Aleatoria Continua $X$ restringida a un intervalo finito $[a,b]$ y su función de probabilidad $f(x)$ tiene una densidad constante sobre este intervalo.
La función de distribución de probabilidad uniforme se define como-

$f(x) = \begin{cases} \frac{1}{b-a}, & a\leq x \leq b\\ 0, & \text{otherwise}\\ \end{cases}$

Uniform Distribution graph

Valor esperado o medio: usando la definición básica de Expectativa, obtenemos:

$\begin{align*} E(x) &= \int \limits_{-\infty}^{\infty} xf(x) dx&\\ &= \int \limits_{a}^{b} \frac{x}{b-a} dx&\\ &= \frac{1}{b-a} \int \limits_{a}^{b} x dx&\\ &= \frac{1}{b-a} \Big[ \frac{x^2}{2}\Big]_{a}^{b}&\\ &= \frac{b^2 - a^2}{2(b-a)}&\\ &= \frac{b + a}{2}&\\ \end{align*}$

Varianza- Usando la fórmula para la varianza- $V(X) = E(X^2) - (E(X))^2$

$\begin{align*} E(x^2) &= \int \limits_{-\infty}^{\infty} x^2f(x) dx&\\ &= \int \limits_{a}^{b} \frac{x^2}{b-a} dx&\\ &= \frac{1}{b-a} \int \limits_{a}^{b} x^2 dx&\\ &= \frac{1}{b-a} \Big[ \frac{x^3}{3}\Big]_{a}^{b}&\\ &= \frac{b^3 - a^3}{3(b-a)}&\\ &= \frac{b^2 + a^2 + ab}{3}&\\ \end{align*}$

Usando este resultado obtenemos –

$\begin{align*} V(x) &= \frac{b^2 + a^2 + ab}{3} - \Big( \frac{b+a}{2}\Big) ^2 &\\ &= \frac{b^2 + a^2 + ab}{3} - \frac{b^2+a^2+2ab}{4} &\\ &= \frac{4b^2 + 4a^2 + 4ab - 3b^2 - 3a^2 - 6ab}{12}&\\ &= \frac{(b-a)^2}{12}&\\ \end{align*}$

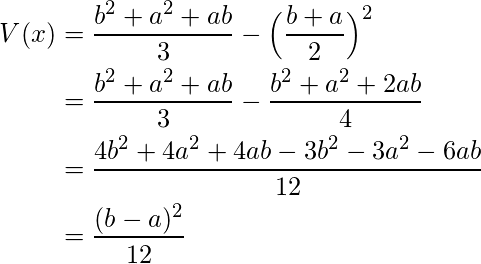
Desviación estándar: según la definición básica de desviación estándar,

$\begin{align*} \sigma &= \sqrt{V(x)} \\&= \frac{b-a}{2\sqrt{3}} \end{align*}$

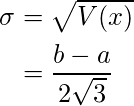
Ejemplo 1: se sabe que la corriente (en mA) medida en un trozo de alambre de cobre sigue una distribución uniforme en el intervalo [0, 25]. Encuentre la fórmula para la función 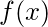$f(x)$ de densidad de probabilidad de la variable aleatoria que 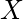$X$ representa la corriente. Calcule la media, la varianza y la desviación estándar de la distribución y encuentre la función de distribución acumulativa $F(x)$ .
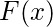Solución: el primer paso es encontrar la función de densidad de probabilidad. Para una distribución Uniforme, 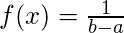$f(x) = \frac{1}{b-a}$ , donde 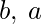$b,\:a$ son el límite superior e inferior respectivamente.
$\therefore \[ f(x) = \begin{cases} \frac{1}{25-0} = 0.04, & 0\leq x\leq 25 \\ 0, & \text{otherwise} \\ \end{cases} \]$

El valor esperado, la varianza y la desviación estándar son:
$E(x) = \frac{b+a}{2} = \frac{25+0}{2} = 12.5 mA\\\\ V(X) = \frac{(b-a)^2}{12} = \frac{(25-0)^2}{12} = 52.08 mA^2\\\\ \text{Standard Deviation} = \sigma = \sqrt{V(x)} = \frac{25}{2\sqrt{3}} = 7.21 mA$
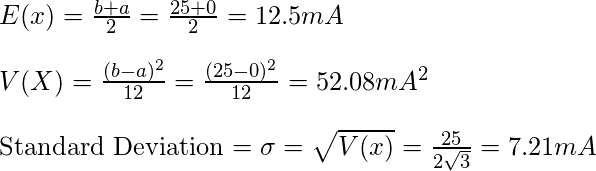
La función de distribución acumulativa se da como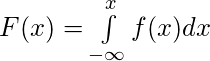
$F(x) = \int \limits_{-\infty}^{x} f(x) dx$
: Hay tres regiones donde se puede definir la CDF,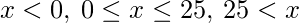 $x<0,\: 0\leq x\leq 25,\:25 < x$

$F(x) = \begin{cases} 0, &x<0\\ \frac{x}{25}, &0\leq x\leq 25\\ 1, &25<x \end{cases}$

Referencias –

Distribución de probabilidad – Wikipedia
Distribución de probabilidad uniforme – statelect.com

Este artículo es una contribución de Chirag Manwani . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta