CRC o Cyclic Redundancy Check es un método para detectar cambios/errores accidentales en el canal de comunicación.
CRC usa Generator Polynomial que está disponible tanto en el lado del remitente como en el del receptor. Un polinomio generador de ejemplo tiene la forma x 3 + x + 1. Este polinomio generador representa la clave 1011. Otro ejemplo es x 2 + 1 que representa la clave 101.
n : Number of bits in data to be sent
from sender side.
k : Number of bits in the key obtained
from generator polynomial.
Lado del remitente (Generación de datos codificados a partir de datos y polinomio generador (o clave)):
- Los datos binarios se aumentan primero agregando k-1 ceros al final de los datos
- Utilice la división binaria de módulo 2 para dividir los datos binarios por la clave y almacenar el resto de la división.
- Agregue el resto al final de los datos para formar los datos codificados y envíe los mismos
Lado del receptor (Compruebe si hay errores introducidos en la transmisión)
Vuelva a realizar la división módulo 2 y si el resto es 0, entonces no hay errores.
En este artículo nos centraremos únicamente en encontrar el resto, es decir, la palabra de control y la palabra clave.
División Módulo 2:
El proceso de división binaria módulo 2 es el mismo que el proceso familiar de división que usamos para números decimales. Solo que en lugar de restar, usamos XOR aquí.
- En cada paso, una copia del divisor (o datos) se somete a XOR con los k bits del dividendo (o clave).
- El resultado de la operación XOR (resto) es (n-1) bits, que se usa para el siguiente paso después de que se extrae 1 bit adicional para que tenga una longitud de n bits.
- Cuando no quedan bits para bajar, tenemos un resultado. El resto de bits (n-1) que se adjunta en el lado del remitente.
Ilustración:
Ejemplo 1 (Sin error en la transmisión):
Data word to be sent - 100100 Key - 1101 [ Or generator polynomial x3 + x2 + 1] Sender Side:

Therefore, the remainder is 001 and hence the encoded data sent is 100100001. Receiver Side: Code word received at the receiver side 100100001
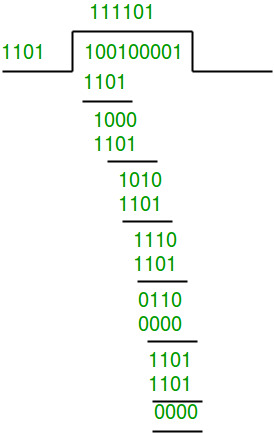
Therefore, the remainder is all zeros. Hence, the data received has no error.
Ejemplo 2: (Error en la transmisión)
Data word to be sent - 100100 Key - 1101 Sender Side:

Therefore, the remainder is 001 and hence the code word sent is 100100001. Receiver Side Let there be an error in transmission media Code word received at the receiver side - 100000001

Dado que el resto no son todos ceros, el error
se detecta en el lado del receptor.
Implementación
Debajo de la implementación para generar una palabra de código a partir de datos binarios y claves dadas.
C++
#include<bits/stdc++.h>
using namespace std;
// Returns XOR of 'a' and 'b'
// (both of same length)
string xor1(string a, string b)
{
// Initialize result
string result = "";
int n = b.length();
// Traverse all bits, if bits are
// same, then XOR is 0, else 1
for(int i = 1; i < n; i++)
{
if (a[i] == b[i])
result += "0";
else
result += "1";
}
return result;
}
// Performs Modulo-2 division
string mod2div(string divident, string divisor)
{
// Number of bits to be XORed at a time.
int pick = divisor.length();
// Slicing the divident to appropriate
// length for particular step
string tmp = divident.substr(0, pick);
int n = divident.length();
while (pick < n)
{
if (tmp[0] == '1')
// Replace the divident by the result
// of XOR and pull 1 bit down
tmp = xor1(divisor, tmp) + divident[pick];
else
// If leftmost bit is '0'.
// If the leftmost bit of the dividend (or the
// part used in each step) is 0, the step cannot
// use the regular divisor; we need to use an
// all-0s divisor.
tmp = xor1(std::string(pick, '0'), tmp) +
divident[pick];
// Increment pick to move further
pick += 1;
}
// For the last n bits, we have to carry it out
// normally as increased value of pick will cause
// Index Out of Bounds.
if (tmp[0] == '1')
tmp = xor1(divisor, tmp);
else
tmp = xor1(std::string(pick, '0'), tmp);
return tmp;
}
// Function used at the sender side to encode
// data by appending remainder of modular division
// at the end of data.
void encodeData(string data, string key)
{
int l_key = key.length();
// Appends n-1 zeroes at end of data
string appended_data = (data +
std::string(
l_key - 1, '0'));
string remainder = mod2div(appended_data, key);
// Append remainder in the original data
string codeword = data + remainder;
cout << "Remainder : "
<< remainder << "\n";
cout << "Encoded Data (Data + Remainder) :"
<< codeword << "\n";
}
// Driver code
int main()
{
string data = "100100";
string key = "1101";
encodeData(data, key);
return 0;
}
// This code is contributed by MuskanKalra1
Python3
# Returns XOR of 'a' and 'b'
# (both of same length)
def xor(a, b):
# initialize result
result = []
# Traverse all bits, if bits are
# same, then XOR is 0, else 1
for i in range(1, len(b)):
if a[i] == b[i]:
result.append('0')
else:
result.append('1')
return ''.join(result)
# Performs Modulo-2 division
def mod2div(dividend, divisor):
# Number of bits to be XORed at a time.
pick = len(divisor)
# Slicing the dividend to appropriate
# length for particular step
tmp = dividend[0 : pick]
while pick < len(dividend):
if tmp[0] == '1':
# replace the dividend by the result
# of XOR and pull 1 bit down
tmp = xor(divisor, tmp) + dividend[pick]
else: # If leftmost bit is '0'
# If the leftmost bit of the dividend (or the
# part used in each step) is 0, the step cannot
# use the regular divisor; we need to use an
# all-0s divisor.
tmp = xor('0'*pick, tmp) + dividend[pick]
# increment pick to move further
pick += 1
# For the last n bits, we have to carry it out
# normally as increased value of pick will cause
# Index Out of Bounds.
if tmp[0] == '1':
tmp = xor(divisor, tmp)
else:
tmp = xor('0'*pick, tmp)
checkword = tmp
return checkword
# Function used at the sender side to encode
# data by appending remainder of modular division
# at the end of data.
def encodeData(data, key):
l_key = len(key)
# Appends n-1 zeroes at end of data
appended_data = data + '0'*(l_key-1)
remainder = mod2div(appended_data, key)
# Append remainder in the original data
codeword = data + remainder
print("Remainder : ", remainder)
print("Encoded Data (Data + Remainder) : ",
codeword)
# Driver code
data = "100100"
key = "1101"
encodeData(data, key)
Javascript
<script>
// A JavaScript program for generating code
// word from given binary data and key.
// Returns XOR of 'a' and 'b'
// (both of same length)
function xor1(a, b)
{
// Initialize result
let result = "";
let n = b.length;
// Traverse all bits, if bits are
// same, then XOR is 0, else 1
for (let i = 1; i < n; i++) {
if (a[i] == b[i]) {
result += "0";
}
else {
result += "1";
}
}
return result;
}
// Performs Modulo-2 division
function mod2div(divident, divisor) {
// Number of bits to be XORed at a time.
let pick = divisor.length;
// Slicing the divident to appropriate
// length for particular step
let tmp = divident.substr(0, pick);
let n = divident.length;
while (pick < n)
{
if (tmp[0] == '1')
{
// Replace the divident by the result
// of XOR and pull 1 bit down
tmp = xor1(divisor, tmp) + divident[pick];
}
else
{
// If leftmost bit is '0'.
// If the leftmost bit of the dividend (or the
// part used in each step) is 0, the step cannot
// use the regular divisor; we need to use an
// all-0s divisor.
let str = "";
for (let i = 0; i < pick; i++) {
str = str.concat('0');
}
tmp = xor1(str, tmp) + divident[pick];
}
// Increment pick to move further
pick += 1;
}
// For the last n bits, we have to carry it out
// normally as increased value of pick will cause
// Index Out of Bounds.
if (tmp[0] == '1') {
tmp = xor1(divisor, tmp);
}
else {
tmp = xor1(string(pick, '0'), tmp);
}
return tmp;
}
// Function used at the sender side to encode
// data by appending remainder of modular division
// at the end of data.
function encodeData(data, key) {
let l_key = key.length;
// Appends n-1 zeroes at end of data
let str = "";
for (let i = 0; i < l_key - 1; i++) {
str = str.concat('0');
}
console.log(str);
let appended_data = data.concat(str);
let remainder = mod2div(appended_data, key);
// Append remainder in the original data
let codeword = data + remainder;
// Adding the print statements
document.write("Remainder : ", remainder);
document.write("Encoded Data (Data + Remainder) :", codeword);
}
// Driver code
{
let data = "100100";
let key = "1101";
encodeData(data, key);
}
// This code is contributed by Gautam goel (gautamgoel962)
</script>
Producción:
Remainder : 001 Encoded Data (Data + Remainder) : 100100001
Complejidad de tiempo: O(n)
Espacio Auxiliar: O(n)
Tenga en cuenta que CRC está diseñado y utilizado principalmente para proteger contra errores comunes en los canales de comunicación y NO es una protección adecuada contra la alteración intencional de datos (consulte las razones aquí )
Implementación mediante manipulación de bits:
la generación de palabras clave CRC también se puede realizar mediante métodos de manipulación de bits de la siguiente manera:
C++
// C++ Program to generate CRC codeword
#include<stdio.h>
#include<iostream>
#include<math.h>
using namespace std;
// function to convert integer to binary string
string toBin(long long int num){
string bin = "";
while (num){
if (num & 1)
bin = "1" + bin;
else
bin = "0" + bin;
num = num>>1;
}
return bin;
}
// function to convert binary string to decimal
long long int toDec(string bin){
long long int num = 0;
for (int i=0; i<bin.length(); i++){
if (bin.at(i)=='1')
num += 1 << (bin.length() - i - 1);
}
return num;
}
// function to compute CRC and codeword
void CRC(string dataword, string generator){
int l_gen = generator.length();
long long int gen = toDec(generator);
long long int dword = toDec(dataword);
// append 0s to dividend
long long int dividend = dword << (l_gen-1);
// shft specifies the no. of least
// significant bits not being XORed
int shft = (int) ceill(log2l(dividend+1)) - l_gen;
long long int rem;
while ((dividend >= gen) || (shft >= 0)){
// bitwise XOR the MSBs of dividend with generator
// replace the operated MSBs from the dividend with
// remainder generated
rem = (dividend >> shft) ^ gen;
dividend = (dividend & ((1 << shft) - 1)) | (rem << shft);
// change shft variable
shft = (int) ceill(log2l(dividend + 1)) - l_gen;
}
// finally, AND the initial dividend with the remainder (=dividend)
long long int codeword = (dword << (l_gen - 1)) | dividend;
cout << "Remainder: " << toBin(dividend) << endl;
cout << "Codeword : " << toBin(codeword) << endl;
}
int main(){
string dataword, generator;
dataword = "10011101";
generator = "1001";
CRC(dataword, generator);
return 0;
}
Java
// Java Program to generate CRC codeword
class GFG {
// function to convert integer to binary string
static String toBin(int num)
{
String bin = "";
while (num > 0) {
if ((num & 1) != 0)
bin = "1" + bin;
else
bin = "0" + bin;
num = num >> 1;
}
return bin;
}
// function to convert binary string to decimal
static int toDec(String bin)
{
int num = 0;
for (int i = 0; i < bin.length(); i++) {
if (bin.charAt(i) == '1')
num += 1 << (bin.length() - i - 1);
}
return num;
}
// function to compute CRC and codeword
static void CRC(String dataword, String generator)
{
int l_gen = generator.length();
int gen = toDec(generator);
int dword = toDec(dataword);
// append 0s to dividend
int dividend = dword << (l_gen - 1);
// shft specifies the no. of least
// significant bits not being XORed
int shft = (int)Math.ceil(Math.log(dividend + 1)
/ Math.log(2))
- l_gen;
int rem;
while ((dividend >= gen) || (shft >= 0)) {
// bitwise XOR the MSBs of dividend with
// generator replace the operated MSBs from the
// dividend with remainder generated
rem = (dividend >> shft) ^ gen;
dividend = (dividend & ((1 << shft) - 1))
| (rem << shft);
// change shft variable
shft = (int)Math.ceil(Math.log(dividend + 1)
/ Math.log(2))
- l_gen;
}
// finally, AND the initial dividend with the
// remainder (=dividend)
int codeword = (dword << (l_gen - 1)) | dividend;
System.out.println("Remainder: " + toBin(dividend));
System.out.println("Codeword : " + toBin(codeword));
}
// Driver Code
public static void main(String[] args)
{
String dataword, generator;
dataword = "10011101";
generator = "1001";
CRC(dataword, generator);
}
}
// This code is contributed by phasing17
Python3
# Python3 program to generate CRC codeword
from math import log, ceil
def CRC(dataword, generator):
dword = int(dataword, 2)
l_gen = len(generator)
# append 0s to dividend
dividend = dword << (l_gen - 1)
# shft specifies the no. of least significant
# bits not being XORed
shft = ceil(log(dividend + 1, 2)) - l_gen
# ceil(log(dividend+1 , 2)) is the no. of binary
# digits in dividend
generator = int(generator, 2)
while dividend >= generator or shft >= 0:
# bitwise XOR the MSBs of dividend with generator
# replace the operated MSBs from the dividend with
# remainder generated
rem = (dividend >> shft) ^ generator
dividend = (dividend & ((1 << shft) - 1)) | (rem << shft)
# change shft variable
shft = ceil(log(dividend+1, 2)) - l_gen
# finally, AND the initial dividend with the remainder (=dividend)
codeword = dword << (l_gen-1)|dividend
print("Remainder:", bin(dividend).lstrip("-0b"))
print("Codeword :", bin(codeword).lstrip("-0b"))
# Driver code
dataword = "10011101"
generator = "1001"
CRC(dataword, generator)
C#
// C# Program to generate CRC codeword
using System;
class GFG {
// function to convert integer to binary string
static string toBin(int num)
{
string bin = "";
while (num > 0) {
if ((num & 1) != 0)
bin = "1" + bin;
else
bin = "0" + bin;
num = num >> 1;
}
return bin;
}
// function to convert binary string to decimal
static int toDec(string bin)
{
int num = 0;
for (int i = 0; i < bin.Length; i++) {
if (bin[i] == '1')
num += 1 << (bin.Length - i - 1);
}
return num;
}
// function to compute CRC and codeword
static void CRC(string dataword, string generator)
{
int l_gen = generator.Length;
int gen = toDec(generator);
int dword = toDec(dataword);
// append 0s to dividend
int dividend = dword << (l_gen - 1);
// shft specifies the no. of least
// significant bits not being XORed
int shft = (int)Math.Ceiling(Math.Log(dividend + 1)
/ Math.Log(2))
- l_gen;
int rem = (dividend >> shft) ^ gen;
while ((dividend >= gen) || (shft >= 0)) {
// bitwise XOR the MSBs of dividend with
// generator replace the operated MSBs from the
// dividend with remainder generated
rem = (dividend >> shft) ^ gen;
dividend = (dividend & ((1 << shft) - 1))
| (rem << shft);
// change shft variable
shft = (int)Math.Ceiling(Math.Log(dividend + 1)
/ Math.Log(2))
- l_gen;
}
// finally, AND the initial dividend with the
// remainder (=dividend)
int codeword = (dword << (l_gen - 1)) | dividend;
Console.WriteLine("Remainder: " + toBin(dividend));
Console.WriteLine("Codeword : " + toBin(codeword));
}
// Driver Code
public static void Main(string[] args)
{
string dataword, generator;
dataword = "10011101";
generator = "1001";
CRC(dataword, generator);
}
}
// This code is contributed by phasing17
Javascript
// JavaScript Program to generate CRC codeword
// function to convert integer to binary string
function toBin(num){
var bin = "";
while (num){
if (num & 1)
bin = "1" + bin;
else
bin = "0" + bin;
num = num>>1;
}
return bin;
}
// function to convert binary string to decimal
function toDec(bin){
var num = 0;
for (var i=0; i<bin.length; i++){
if (bin[i]=='1')
num += 1 << (bin.length - i - 1);
}
return num;
}
// function to compute CRC and codeword
function CRC(dataword, generator){
var l_gen = generator.length;
var gen = toDec(generator);
var dword = toDec(dataword);
// append 0s to dividend
var dividend = dword << (l_gen-1);
// shft specifies the no. of least
// significant bits not being XORed
var shft = Math.ceil(Math.log2(dividend+1)) - l_gen;
var rem;
while ((dividend >= gen) || (shft >= 0)){
// bitwise XOR the MSBs of dividend with generator
// replace the operated MSBs from the dividend with
// remainder generated
rem = (dividend >> shft) ^ gen;
dividend = (dividend & ((1 << shft) - 1)) | (rem << shft);
// change shft variable
shft = Math.ceil(Math.log2(dividend + 1)) - l_gen;
}
// finally, AND the initial dividend with the remainder (=dividend)
var codeword = (dword << (l_gen - 1)) | dividend;
console.log( "Remainder:", toBin(dividend));
console.log("Codeword :", toBin(codeword));
}
//Driver code
var dataword = "10011101";
var generator = "1001";
CRC(dataword, generator);
//This code is contributed by phasing17
Remainder: 100 Codeword : 10011101100
Complejidad de tiempo: O(n)
Espacio Auxiliar: O(n)
Referencias:
https://en.wikipedia.org/wiki/Cyclic_redundancy_check
Este artículo es una contribución de Jay Patel . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo y enviarlo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA