Prerrequisito: Árbol de expresión
El árbol de expresión es un árbol binario en el que cada Node interno corresponde al operador y cada Node hoja corresponde al operando, por lo que, por ejemplo, el árbol de expresión para 3 + ((5+9)*2) sería:
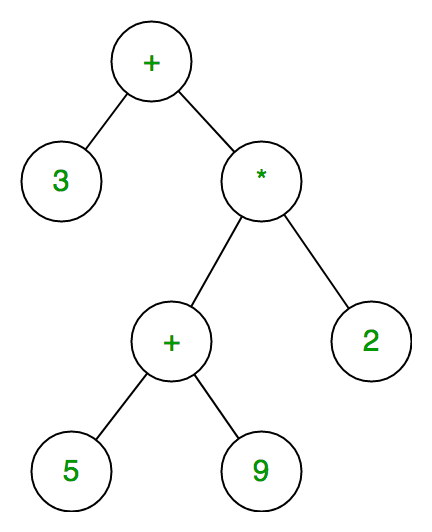
En los árboles de expresión, los Nodes hoja son operandos y los Nodes no hoja son operadores. Eso significa que un árbol de expresión es un árbol binario donde los Nodes internos son operadores y las hojas son operandos. Un árbol de expresión consta de expresiones binarias. Pero para un operador unario, un subárbol estará vacío.
Construcción del árbol de expresión:
- El usuario proporcionará una expresión de sufijo para la cual el programa construirá el árbol de expresión.
- El recorrido en orden del árbol binario/árbol de expresión proporcionará una expresión infija de la entrada dada.
Ejemplo:
Input: A B C*+ D/ Output: A + B * C / D
Paso 1: Los primeros tres símbolos son operandos, así que cree Nodes de árbol y empuje los punteros hacia ellos en una pila como se muestra a continuación.
Paso 2: en el siguiente paso, se leerá un operador ‘*’, por lo que se extraen dos punteros a los árboles, se forma un nuevo árbol y se empuja un puntero a la pila.
Paso 3: en el siguiente paso, se leerá un operador ‘+’, por lo que se extraen dos punteros a los árboles, se forma un nuevo árbol y se coloca un puntero en la pila.
Paso 4: De manera similar, como en los casos anteriores, primero empujamos ‘D’ en la pila y luego en el último paso primero, leeremos ‘/’ y luego, como paso anterior, aparecerá el elemento superior y luego será el subárbol derecho de la raíz ‘/ ‘ y el otro Node será el subárbol derecho.
El árbol de expresiones construidas final es:
A continuación se muestra el programa C++ para implementar el enfoque anterior:
C++
// C++ program to implement
// the above approach
#include <bits/stdc++.h>
using namespace std;
class node {
public:
char value;
node* left;
node* right;
node* next = NULL;
node(char c)
{
this->value = c;
left = NULL;
right = NULL;
}
node()
{
left = NULL;
right = NULL;
}
friend class Stack;
friend class expression_tree;
};
// Class stack to hold
// tree nodes
class Stack {
node* head = NULL;
public:
void push(node*);
node* pop();
friend class expression_tree;
};
// Class to implement
// inorder traversal
class expression_tree {
public:
// Function to implement
// inorder traversal
void inorder(node* x)
{
if (x == NULL)
return;
else {
inorder(x->left);
cout << x->value << " ";
inorder(x->right);
}
}
};
// Function to push values
// onto the stack
void Stack::push(node* x)
{
if (head == NULL) {
head = x;
}
// We are inserting nodes at
// the top of the stack [
// following LIFO principle]
else {
x->next = head;
head = x;
}
}
// Function to implement pop
// operation in the stack
node* Stack::pop()
{
// Poping out the top most[
// pointed with head] element
node* p = head;
head = head->next;
return p;
}
// Driver code
int main()
{
// Postfix expression
string s = "ABC*+D/";
Stack e;
expression_tree a;
node *x, *y, *z;
int l = s.length();
for (int i = 0; i < l; i++) {
// if read character is operator
// then poping two other elements
// from stack and making a binary
// tree
if (s[i] == '+' || s[i] == '-'
|| s[i] == '*' || s[i] == '/'
|| s[i] == '^') {
z = new node(s[i]);
x = e.pop();
y = e.pop();
z->left = y;
z->right = x;
e.push(z);
}
else {
z = new node(s[i]);
e.push(z);
}
}
// Print the inorder traversal
cout << " The Inorder Traversal of Expression Tree: ";
a.inorder(z);
return 0;
}
El recorrido en orden del árbol de expresión: A + B * C / D
Publicación traducida automáticamente
Artículo escrito por kunjparekh310 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA



