En este artículo, veremos cómo calcular el promedio móvil en un marco de datos de pandas. La media móvil calcula el promedio de los datos durante un período de tiempo. El promedio móvil también se conoce como la media móvil y se calcula promediando los datos de la serie de tiempo dentro de k períodos de tiempo.
Hay tres tipos de medias móviles:
- Promedio móvil simple (SMA)
- Media Móvil Exponencial (EMA)
- Promedio móvil acumulativo (CMA)
El enlace a los datos utilizados es RELIANCE.NS_
Promedio móvil simple (SMA)
Un promedio móvil simple nos dice la media no ponderada de los K puntos de datos anteriores. Cuanto mayor es el valor de K, más suave es la curva, pero aumentar K disminuye la precisión. Si los puntos de datos son p 1, p 2 , . . . , p n entonces calculamos la media móvil simple.

En Python, podemos calcular el promedio móvil usando el método .rolling(). Este método proporciona ventanas móviles sobre los datos, y podemos usar la función media sobre estas ventanas para calcular los promedios móviles. El tamaño de la ventana se pasa como parámetro en la función .rolling(window).
Ahora veamos un ejemplo de cómo calcular una media móvil simple durante un período de 30 días.
Paso 1: Importación de bibliotecas
Python3
# importing Libraries
# importing pandas as pd
import pandas as pd
# importing numpy as np
# for Mathematical calculations
import numpy as np
# importing pyplot from matplotlib as plt
# for plotting graphs
import matplotlib.pyplot as plt
plt.style.use('default')
%matplotlib inline
Paso 2: Importación de datos
Para importar datos usaremos pandas. función read_csv() .
Python3
# importing time-series data
reliance = pd.read_csv('RELIANCE.NS.csv', index_col='Date',
parse_dates=True)
# Printing dataFrame
reliance.head()
Producción:

Paso 3: Cálculo de la media móvil simple
Para calcular SMA en Python usaremos la función pandas dataframe.rolling() que nos ayuda a hacer cálculos en una ventana móvil. En la ventana móvil, usaremos la función .mean() para calcular la media de cada ventana.
Sintaxis: DataFrame.rolling(ventana, min_periods=Ninguno, centro=Falso, win_type=Ninguno, on=Ninguno, eje=0).mean()
Parámetros:
- ventana : Tamaño de la ventana. Esa es la cantidad de observaciones que tenemos que tomar para el cálculo de cada ventana.
- min_periods : menor número de observaciones en una ventana requerida para tener un valor (de lo contrario, el resultado es NA).
- center : Se utiliza para colocar las etiquetas en el centro de la ventana.
- win_type: se utiliza para establecer el tipo de ventana.
- on: columna de fecha y hora de nuestro marco de datos en el que tenemos que calcular la media móvil.
- eje: entero o string, por defecto 0
Python3
# updating our dataFrame to have only # one column 'Close' as rest all columns # are of no use for us at the moment # using .to_frame() to convert pandas series # into dataframe. reliance = reliance['Close'].to_frame() # calculating simple moving average # using .rolling(window).mean() , # with window size = 30 reliance['SMA30'] = reliance['Close'].rolling(30).mean() # removing all the NULL values using # dropna() method reliance.dropna(inplace=True) # printing Dataframe reliance
Producción:

Paso 4: Trazado de promedios móviles simples
Python3
# plotting Close price and simple # moving average of 30 days using .plot() method reliance[['Close', 'SMA30']].plot(label='RELIANCE', figsize=(16, 8))
Producción:

Promedio móvil acumulativo (CMA)
La media móvil acumulativa es la media de todos los valores anteriores hasta el valor actual. CMA de dataPoints x 1 , x 2 ….. en el tiempo t se puede calcular como,

Mientras calculamos CMA, no tenemos un tamaño fijo de la ventana. El tamaño de la ventana sigue aumentando a medida que pasa el tiempo. En Python, podemos calcular CMA usando el método .expanding(). Ahora vamos a ver un ejemplo, para calcular CMA para un periodo de 30 días.
Paso 1: Importación de bibliotecas
Python3
# importing Libraries
# importing pandas as pd
import pandas as pd
# importing numpy as np
# for Mathematical calculations
import numpy as np
# importing pyplot from matplotlib as plt
# for plotting graphs
import matplotlib.pyplot as plt
plt.style.use('default')
%matplotlib inline
Paso 2: Importación de datos
Para importar datos usaremos la función pandas .read_csv().
Python3
# importing time-series data
reliance = pd.read_csv('RELIANCE.NS.csv',
index_col='Date',
parse_dates=True)
# Printing dataFrame
reliance.head()
Paso 3: Cálculo de la media móvil acumulativa
Para calcular CMA en Python usaremos la función dataframe.expanding(). Este método nos da el valor acumulativo de nuestra función de agregación (media en este caso).
Sintaxis: DataFrame.expanding(min_periods=1, center=Ninguno, axis=0, method=’single’).mean()
Parámetros:
- min_periods: int, predeterminado 1. Se requiere el menor número de observaciones en una ventana para tener un valor (de lo contrario, el resultado es NA).
- centro: booleano, por defecto Falso. Se utiliza para colocar las etiquetas en el centro de la ventana.
- eje: int o str, por defecto 0
- método: str {‘único’, ‘tabla’}, por defecto ‘único’
Python3
# updating our dataFrame to have only # one column 'Close' as rest all columns # are of no use for us at the moment # using .to_frame() to convert pandas series # into dataframe. reliance = reliance['Close'].to_frame() # calculating cumulative moving # average using .expanding().mean() reliance['CMA30'] = reliance['Close'].expanding().mean() # printing Dataframe reliance
Producción:

Paso 4: Trazado de promedios móviles acumulativos
Python3
# plotting Close price and cumulative moving # average of 30 days using .plot() method reliance[['Close', 'CMA30']].plot(label='RELIANCE', figsize=(16, 8))
Producción:
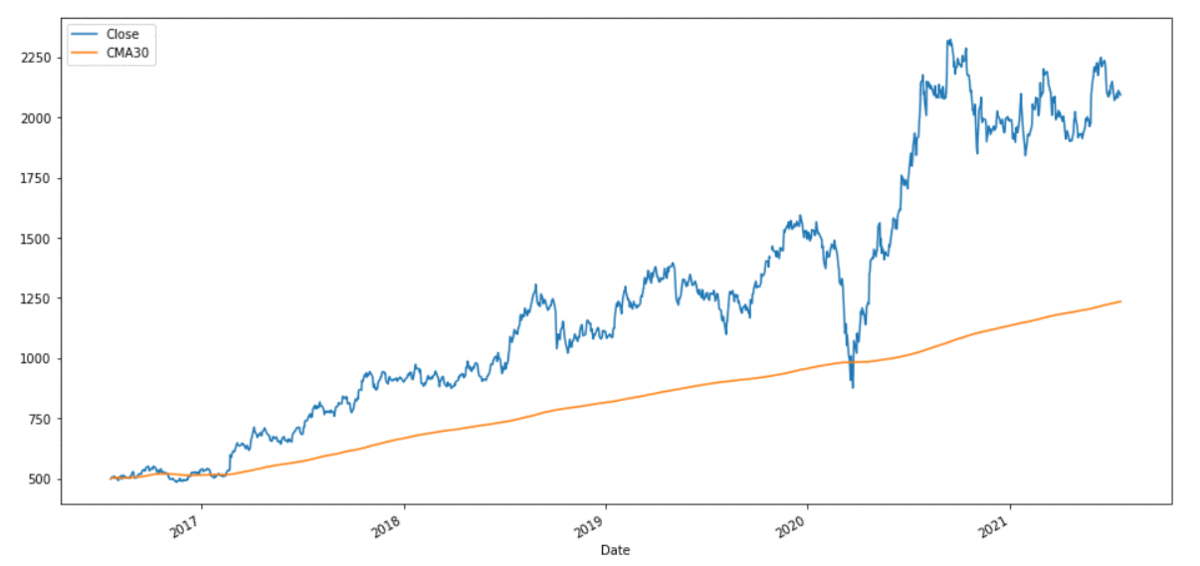
Media móvil exponencial (EMA):
La media móvil exponencial (EMA) nos dice la media ponderada de los K puntos de datos anteriores. EMA otorga un mayor peso e importancia a los puntos de datos más recientes. La fórmula para calcular la EMA en el período de tiempo t es:

donde x t es el valor de la observación en el momento t & α es el factor de suavizado. En Python, la EMA se calcula utilizando el método .ewm(). Podemos pasar span o window como parámetro al método .ewm(span = ).
Ahora veremos un ejemplo para calcular la EMA para un período de 30 días.
Paso 1: Importación de bibliotecas
Python3
# importing Libraries
# importing pandas as pd
import pandas as pd
# importing numpy as np
# for Mathematical calculations
import numpy as np
# importing pyplot from matplotlib as plt
# for plotting graphs
import matplotlib.pyplot as plt
plt.style.use('default')
%matplotlib inline
Paso 2: Importación de datos
Para importar datos usaremos la función pandas .read_csv().
Python3
# importing time-series data
reliance = pd.read_csv('RELIANCE.NS.csv',
index_col='Date',
parse_dates=True)
# Printing dataFrame
reliance.head()
Producción:

Paso 3: Cálculo de la media móvil exponencial
Para calcular EMA en Python usamos la función dataframe.ewm(). Nos proporciona funciones ponderadas exponencialmente. Usaremos la función .mean() para calcular la EMA.
Sintaxis: DataFrame.ewm(com=Ninguno, span=Ninguno, halflife=Ninguno, alpha=Ninguno, min_periods=0, adjust=True, ignore_na=False, axis=0, times=Ninguno).mean()
Parámetros:
- com: flotante, opcional. Es el decaimiento en términos del centro de masa.
- span: float, opcional. Es la decadencia en términos de lapso.
- vida media: float, str, timedelta, opcional. Es la decadencia en términos de vida media.
- alfa: flotante, opcional. Es el factor de suavizado que tiene un valor entre 0 y 1, 1 inclusive.
- min_periods : int, predeterminado 0. Se requiere el menor número de observaciones en una ventana para tener un valor (de lo contrario, el resultado es NA).
- ajustar: bool, por defecto True. Dividir por el factor de ajuste decreciente en los períodos iniciales para tener en cuenta el desequilibrio en las ponderaciones relativas (ver EWMA como un promedio móvil)
- ignore_na: ignora los valores faltantes al calcular los pesos; especifique True para reproducir el comportamiento anterior a 0.15.0.
- eje : El eje a utilizar. El valor 0 identifica las filas y 1 identifica las columnas.
Python3
# updating our dataFrame to have only # one column 'Close' as rest all columns # are of no use for us at the moment # using .to_frame() to convert pandas # series into dataframe. reliance = reliance['Close'].to_frame() # calculating exponential moving average # using .ewm(span).mean() , with window size = 30 reliance['EWMA30'] = reliance['Close'].ewm(span=30).mean() # printing Dataframe reliance
Producción:

Paso 4: Trazado de medias móviles exponenciales
Python3
# plotting Close price and exponential # moving averages of 30 days # using .plot() method reliance[['Close', 'EWMA30']].plot(label='RELIANCE', figsize=(16, 8))
Producción:

Publicación traducida automáticamente
Artículo escrito por bistpratham y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA