Requisito previo: Anillos
Homomorfismo de anillo:
un conjunto ![]() con dos operaciones binarias en el conjunto
con dos operaciones binarias en el conjunto ![]() let denotado por
let denotado por ![]() y
y ![]() se llama anillo denotado como
se llama anillo denotado como ![]() , si
, si ![]() es un grupo abeliano y
es un grupo abeliano y ![]() es un semigrupo, que también siguen las leyes distributivas derecha e izquierda.
es un semigrupo, que también siguen las leyes distributivas derecha e izquierda.
para dos anillos ![]() y
y ![]() [Tex]\times [/Tex]
[Tex]\times [/Tex] ![]() una aplicación
una aplicación ![]() se denomina homomorfismo de anillos si
se denomina homomorfismo de anillos si
 , ∀a, segundo ∈
, ∀a, segundo ∈ 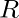 .
.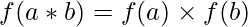 , ∀a, segundo ∈
, ∀a, segundo ∈ 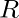 .
. [Tex]( [/Tex]I R
[Tex]( [/Tex]I R
 I S , si I R e I S son identidades (si existen que en el caso de Ring con unidad) de operaciones set
I S , si I R e I S son identidades (si existen que en el caso de Ring con unidad) de operaciones set 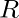 over
over 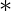 y set
y set 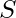 over
over 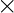 respectivamente.
respectivamente.
NOTA: El anillo ![]() se llama imagen homomórfica del anillo
se llama imagen homomórfica del anillo ![]() .
.
Ejemplos:
- Función f(x) = x mod(n) del grupo (
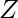 ,+,*) a (
,+,*) a ( 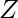 n ,+,*) ∀x ∈
n ,+,*) ∀x ∈ 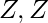 es un grupo de enteros. + y * son operaciones simples de suma y multiplicación respectivamente.
es un grupo de enteros. + y * son operaciones simples de suma y multiplicación respectivamente. - Función f(x) = x para cualquiera de los dos grupos (R,+,*) y (S,⨁,
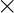 ) ∀x ∈ R, lo que se denomina homomorfismo de anillos de identidad.
) ∀x ∈ R, lo que se denomina homomorfismo de anillos de identidad. - Función f(x) = 0 para grupos (N,*,+) y (Z,*,+) para ∀x ∈ N.
- Función f(x) = que es un grupo de forma conjugada compleja (C,+,*) consigo mismo, aquí C es un conjunto de números complejos. + y * son operaciones simples de suma y multiplicación respectivamente.
NOTA: Si f es homomorfismo de (R,+,*) y (S,⨁, ![]() ) entonces f(O R ) = f(O S ) donde O R y O S son identidades del conjunto R sobre + y el conjunto S sobre ⨁ operaciones respectivamente.
) entonces f(O R ) = f(O S ) donde O R y O S son identidades del conjunto R sobre + y el conjunto S sobre ⨁ operaciones respectivamente.
NOTA: Si f es homomorfismo de anillos de (R,+,*) y (S,⨁, ![]() ) entonces f : (R,+) → (S,⨁) es homomorfismo de grupos.
) entonces f : (R,+) → (S,⨁) es homomorfismo de grupos.
Isomorfismo de anillo:
un homomorfismo de uno y otro de anillo ![]() a anillo
a anillo ![]() se llama isomorfismo de anillo,
se llama isomorfismo de anillo, ![]() y
y ![]() son isomorfos.
son isomorfos.
Automorfismo de anillos:
Un homomorfismo de un anillo a sí mismo se llama Automorfismo de anillos.
Homomorfismo de campo:
para dos campos ![]() y
y ![]() una aplicación
una aplicación ![]() se llama homomorfismo de campo si
se llama homomorfismo de campo si
 , ∀a, segundo ∈
, ∀a, segundo ∈ 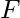 .
.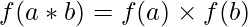 , ∀a, segundo ∈
, ∀a, segundo ∈ 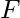 .
. I F
I F
 I K , donde I F e I K son identidades de operaciones de
I K , donde I F e I K son identidades de operaciones de 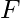 reposición
reposición 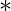 y
y 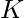 reposición
reposición 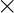 respectivamente.
respectivamente. O F
O F
 O K , donde OF y OK son identidades de las operaciones set
O K , donde OF y OK son identidades de las operaciones set 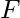 over
over 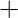 y set
y set 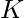 over
over  respectivamente.
respectivamente.
Publicación traducida automáticamente
Artículo escrito por ohiamvaibhav y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA