Clasificación mediante la combinación de algoritmos de ordenación por inserción y ordenación por fusión

Clasificación por inserción : la array se divide virtualmente en una parte ordenada y otra no ordenada. Los valores de la parte no ordenada se seleccionan y colocan en la posición correcta en la parte ordenada.
Ventajas: Las siguientes son las ventajas del ordenamiento por inserción:

• Si el tamaño de la lista que se va a ordenar es pequeño, la ordenación por inserción se ejecuta más rápido
• La ordenación por inserción toma tiempo O(N) cuando los elementos ya están ordenados
• Es un algoritmo en el lugar O (1), no se requiere espacio auxiliar

Merge sort : Merge Sort es un algoritmo Divide and Conquer . Divide la array de entrada en dos mitades, se llama a sí mismo para las dos mitades y luego fusiona las dos mitades ordenadas.

Ventajas: Las siguientes son las ventajas de la ordenación por fusión:

• La división del problema principal en subproblema no tiene mayor coste

A partir de las dos comparaciones anteriores, se pueden combinar las ventajas de ambos algoritmos de clasificación, y el algoritmo resultante tendrá una complejidad de tiempo O(N[K+log(N/K)]). A continuación se muestra la derivación de la complejidad temporal de este algoritmo combinado:
Let, no. de elementos en la lista = N
Divide :

• Primero dividimos estos N elementos en (N/K) grupos de tamaño K

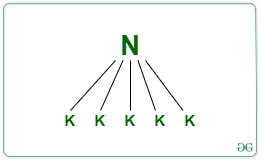
Clasificación :

• Para cada división de subarreglo de tamaño K, realice la operación de ordenación por inserción para ordenar este subarreglo
• El costo total de la ordenación por inserción para un solo bloque de K elementos:
  • Para el mejor de los casos: O(K)
  • Para el peor de los casos: O(
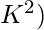
• Dado que hay (N/K) bloques de este tipo, cada uno de tamaño K, obtenemos el costo total de aplicar la ordenación por inserción como:
  • En el mejor de los casos: (N/K) * K = O(N) <– (1)
  • Para el peor de los casos: (N/K) * K^{2} = O(NK) <– (2)

Fusionando :

• Después de aplicar la ordenación por inserción en (N/K) agrupa cada uno de los K elementos ordenados
• Para fusionar estos grupos (N/K):

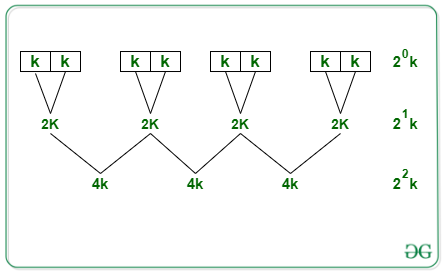
• Digamos que tomamos i iteraciones de tipo de fusión. Entonces, para que el ciclo se detenga, necesitaremos igualar como:
• (2^i) * K = N
• (2^i) = N/K
• i*log(2) = log(N/K) Tomando log en ambos lados
• yo = registro (N/K)
• Costo de fusión = O(N)
• Costo total de fusión = No. de iteración * Costo de iteración
  • = log(N/K)*N
  • = N*log(N/K)
  • = O(N*Log(N/K)) <– (3)

El costo total del algoritmo (inserción + fusión) es:

• Mejor caso: N+Nlog(N/K) <– de (1) y (3)
• Peor caso: NK + Nlog(N/K) <– de (2) y (3)

Si K = 1, entonces es una ordenación por fusión completa, que es mejor en términos de complejidad de tiempo
Si K = N, entonces es una ordenación por inserción completa, que es mejor en términos de complejidad de espacio