C# Programa para Programa para rotación de arrays

Escribe una función rotar(ar[], d, n) que gire arr[] de tamaño n por d elementos. 
 

La rotación de la array anterior por 2 hará que la array
 

MÉTODO 1 (usando array temporal) 

Input arr[] = [1, 2, 3, 4, 5, 6, 7], d = 2, n =7
1) Store the first d elements in a temp array
   temp[] = [1, 2]
2) Shift rest of the arr[]
   arr[] = [3, 4, 5, 6, 7, 6, 7]
3) Store back the d elements
   arr[] = [3, 4, 5, 6, 7, 1, 2]

Complejidad temporal : O(n) 
Espacio auxiliar : O(d)

MÉTODO 2 (Rotar uno por uno)  

leftRotate(arr[], d, n)
start
  For i = 0 to i < d
    Left rotate all elements of arr[] by one
end

Para rotar por uno, almacene arr[0] en una variable temporal temp, mueva arr[1] a arr[0], arr[2] a arr[1] …y finalmente temp a arr[n-1]
Tomemos el mismo ejemplo arr[] = [1, 2, 3, 4, 5, 6, 7], d = 2 
Rotar arr[] por uno 2 veces 
Obtenemos [2, 3, 4, 5, 6, 7, 1 ] después de la primera rotación y [ 3, 4, 5, 6, 7, 1, 2] después de la segunda rotación.
A continuación se muestra la implementación del enfoque anterior: 
 

// C# program for array rotation
using System;
 
class GFG {
    /* Function to left rotate arr[]
    of size n by d*/
    static void leftRotate(int[] arr, int d,
                           int n)
    {
        for (int i = 0; i < d; i++)
            leftRotatebyOne(arr, n);
    }
 
    static void leftRotatebyOne(int[] arr, int n)
    {
        int i, temp = arr[0];
        for (i = 0; i < n - 1; i++)
            arr[i] = arr[i + 1];
 
        arr[n-1] = temp;
    }
 
    /* utility function to print an array */
    static void printArray(int[] arr, int size)
    {
        for (int i = 0; i < size; i++)
            Console.Write(arr[i] + " ");
    }
 
    // Driver code
    public static void Main()
    {
        int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
        leftRotate(arr, 2, 7);
        printArray(arr, 7);
    }
}
 
// This code is contributed by Sam007

Producción :  

3 4 5 6 7 1 2 

Complejidad del tiempo: O(n * d) 
Espacio auxiliar: O(1)
MÉTODO 3 (Un algoritmo de malabarismo) 
Esta es una extensión del método 2. En lugar de mover uno por uno, divida la array en diferentes conjuntos 
donde el número de conjuntos sea igual a GCD de n y d y mover los elementos dentro de los conjuntos. 
Si GCD es 1 como es para la array de ejemplo anterior (n = 7 y d = 2), entonces los elementos se moverán dentro de un solo conjunto, simplemente comenzamos con temp = arr[0] y seguimos moviendo arr[I+d] para llegar [I] y finalmente almacenar la temperatura en el lugar correcto.
Aquí hay un ejemplo para n = 12 y d = 3. GCD es 3 y 
 

Let arr[] be {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}

a) Elements are first moved in first set – (See below 
   diagram for this movement)

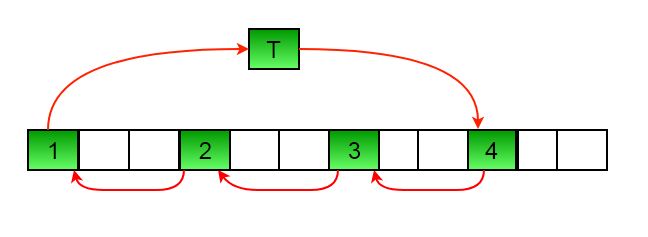
          arr[] after this step --> {4 2 3 7 5 6 10 8 9 1 11 12}

b)    Then in second set.
          arr[] after this step --> {4 5 3 7 8 6 10 11 9 1 2 12}

c)    Finally in third set.
          arr[] after this step --> {4 5 6 7 8 9 10 11 12 1 2 3}

A continuación se muestra la implementación del enfoque anterior:
 

// C# program for array rotation
using System;
 
class GFG {
    /* Function to left rotate arr[]
    of size n by d*/
    static void leftRotate(int[] arr, int d,
                           int n)
    {
        int i, j, k, temp;
        /* To handle if d >= n */
        d = d % n;
        int g_c_d = gcd(d, n);
        for (i = 0; i < g_c_d; i++) {
            /* move i-th values of blocks */
            temp = arr[i];
            j = i;
            while (true) {
                k = j + d;
                if (k >= n)
                    k = k - n;
                if (k == i)
                    break;
                arr[j] = arr[k];
                j = k;
            }
            arr[j] = temp;
        }
    }
 
    /*UTILITY FUNCTIONS*/
    /* Function to print an array */
    static void printArray(int[] arr, int size)
    {
        for (int i = 0; i < size; i++)
            Console.Write(arr[i] + " ");
    }
 
    /* Function to get gcd of a and b*/
    static int gcd(int a, int b)
    {
        if (b == 0)
            return a;
        else
            return gcd(b, a % b);
    }
 
    // Driver code
    public static void Main()
    {
        int[] arr = { 1, 2, 3, 4, 5, 6, 7 };
        leftRotate(arr, 2, 7);
        printArray(arr, 7);
    }
}
 
// This code is contributed by Sam007

Producción : 

3 4 5 6 7 1 2 

Complejidad temporal : O(n) 
Espacio auxiliar : O(1)
 

Consulte las siguientes publicaciones para conocer otros métodos de rotación de arrays: 
Algoritmo de intercambio de bloques para rotación de arrays  
Algoritmo de inversión para rotación de arrays
Escriba comentarios si encuentra algún error en los programas/algoritmos anteriores.
 

¡ Consulte el artículo completo sobre el programa para la rotación de arrays para obtener más detalles!