El índice de equilibrio de una array es un índice tal que la suma de los elementos en los índices más bajos es igual a la suma de los elementos en los índices más altos. Por ejemplo, en una array A:
Ejemplo :
Entrada : A[] = {-7, 1, 5, 2, -4, 3, 0}
Salida : 3
3 es un índice de equilibrio, porque:
A[0] + A[1] + A[2] = A [4] + A[5] + A[6]Entrada : A[] = {1, 2, 3}
Salida : -1
Escribe una función int equilibrio(int[] arr, int n) ; que dada una secuencia arr[] de tamaño n, devuelve un índice de equilibrio (si lo hay) o -1 si no existen índices de equilibrio.
Método 1 (Simple pero ineficiente)
Use dos bucles. El bucle externo itera a través de todo el elemento y el bucle interno descubre si el índice actual elegido por el bucle externo es un índice de equilibrio o no. La complejidad temporal de esta solución es O(n^2).
Python3
# Python program to find equilibrium # index of an array # function to find the equilibrium index def equilibrium(arr): leftsum = 0 rightsum = 0 n = len(arr) # Check for indexes one by one # until an equilibrium index is found for i in range(n): leftsum = 0 rightsum = 0 # get left sum for j in range(i): leftsum += arr[j] # get right sum for j in range(i + 1, n): rightsum += arr[j] # if leftsum and rightsum are same, # then we are done if leftsum == rightsum: return i # return -1 if no equilibrium index is found return -1 # driver code arr = [-7, 1, 5, 2, -4, 3, 0] print (equilibrium(arr)) # This code is contributed by Abhishek Sharama
3
Complejidad del tiempo: O(n^2)
Método 2 (complicado y eficiente)
La idea es obtener primero la suma total de la array. Luego itere a través de la array y siga actualizando la suma izquierda que se inicializa como cero. En el ciclo, podemos obtener la suma correcta restando los elementos uno por uno. Gracias a Sambasiva por sugerir esta solución y proporcionar el código para esto.
1) Initialize leftsum as 0
2) Get the total sum of the array as sum
3) Iterate through the array and for each index i, do following.
a) Update sum to get the right sum.
sum = sum - arr[i]
// sum is now right sum
b) If leftsum is equal to sum, then return current index.
// update leftsum for next iteration.
c) leftsum = leftsum + arr[i]
4) return -1
// If we come out of loop without returning then
// there is no equilibrium index
La siguiente imagen muestra la ejecución en seco del enfoque anterior:
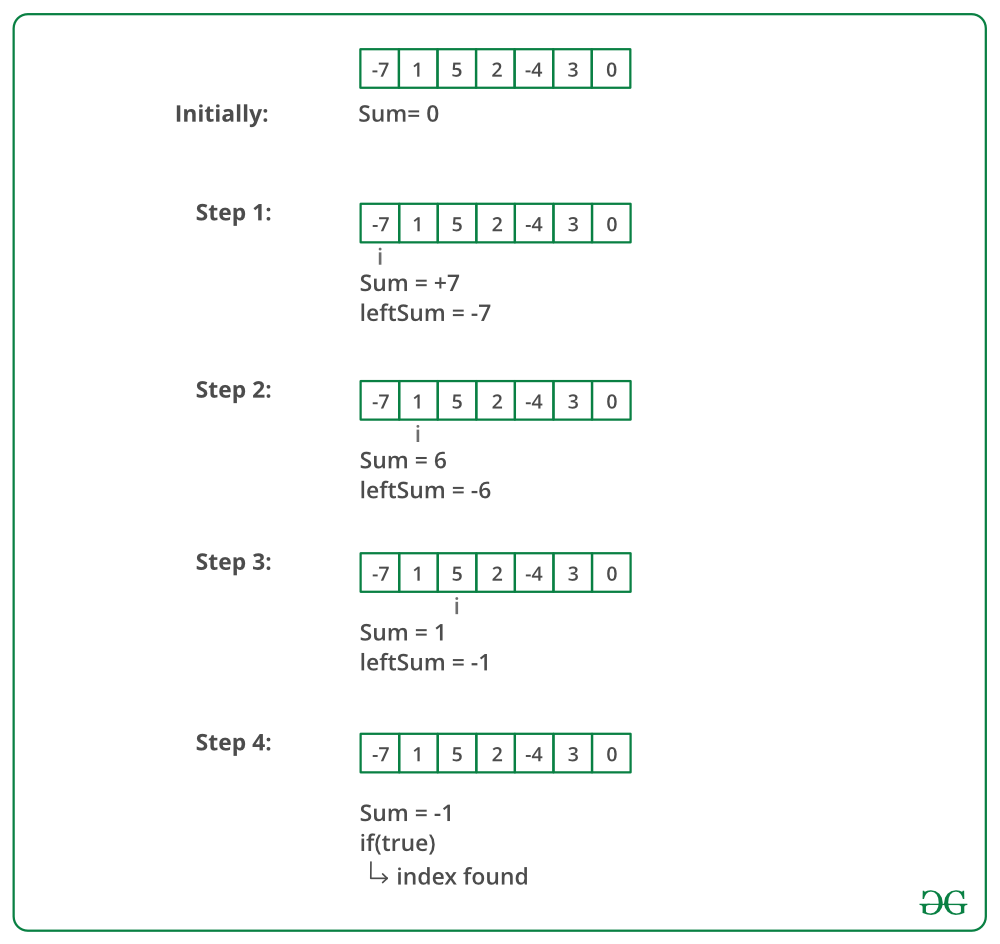
A continuación se muestra la implementación del enfoque anterior:
Python3
# Python program to find the equilibrium
# index of an array
# function to find the equilibrium index
def equilibrium(arr):
# finding the sum of whole array
total_sum = sum(arr)
leftsum = 0
for i, num in enumerate(arr):
# total_sum is now right sum
# for index i
total_sum -= num
if leftsum == total_sum:
return i
leftsum += num
# If no equilibrium index found,
# then return -1
return -1
# Driver code
arr = [-7, 1, 5, 2, -4, 3, 0]
print ('First equilibrium index is ',
equilibrium(arr))
# This code is contributed by Abhishek Sharma
First equilibrium index is 3
Salida: El
primer índice de equilibrio es 3
Complejidad de tiempo: O(n)
Método 3:
Este es un método bastante simple y directo. La idea es tomar la suma del prefijo de la array dos veces. Una vez desde el extremo frontal de la array y otra desde la parte posterior de la array.
Después de tomar ambas sumas de prefijos, ejecute un ciclo y verifique si hay alguna i si la suma de prefijos de una array es igual a la suma de prefijos de la segunda array, entonces ese punto puede considerarse como el punto de equilibrio.
Python3
# Python program to find the equilibrium
# index of an array
# Function to find the equilibrium index
def equilibrium(arr):
left_sum = []
right_sum = []
# Iterate from 0 to len(arr)
for i in range(len(arr)):
# If i is not 0
if(i):
left_sum.append(left_sum[i-1]+arr[i])
right_sum.append(right_sum[i-1]+arr[len(arr)-1-i])
else:
left_sum.append(arr[i])
right_sum.append(arr[len(arr)-1])
# Iterate from 0 to len(arr)
for i in range(len(arr)):
if(left_sum[i] == right_sum[len(arr) - 1 - i ]):
return(i)
# If no equilibrium index found,then return -1
return -1
# Driver code
arr = [-7, 1, 5, 2, -4, 3, 0]
print('First equilibrium index is ',
equilibrium(arr))
# This code is contributed by Lokesh Sharma
First Point of equilibrium is at index 3
Complejidad de tiempo: O(N)
Complejidad espacial: O(N)
Consulte el artículo completo sobre el índice de equilibrio de una array para obtener más detalles.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA