Dado un número N y una array 2D infinita , que se completará con el algoritmo que se indica a continuación, la tarea es encontrar las coordenadas del elemento dado presente en la array. El algoritmo es como sigue:
- La celda más a la izquierda y más arriba de la array se llena con 1. Luego, todas las celdas se llenan con números consecutivos a partir de 2
- La celda sin llenar más a la izquierda en la primera fila está llena. Luego, mientras se llena el vecino izquierdo de la última celda llena, las celdas debajo de él se llenan a continuación, hasta que la última celda llena tenga un vecino izquierdo no lleno
- A continuación, las celdas se rellenan de derecha a izquierda hasta la primera columna. Luego, nuevamente se llena la celda sin llenar más a la izquierda en la primera fila
- Los dos pasos anteriores se repiten infinitamente.
Ejemplos:
Entrada: N = 12
Salida: 3 4
Explicación: 12 se encuentra en la celda con fila como 3 y columna como 4Entrada: N = 10549857
Salida: 353 3249
Explicación: 10549857 se encuentra en la celda con fila como 353 y columna como 3249
Enfoque: Se pueden hacer las siguientes observaciones:
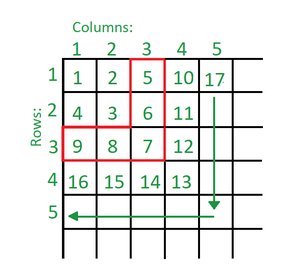
- En la imagen de arriba, la parte resaltada en rojo o ‘L invertida’ formada por la 3.ª fila y la 3.ª columna consta de todos los números mayores que 4 y menores que 10. De manera similar, la ‘L invertida’ formada por la 4.ª fila y la 4.ª columna consta de números mayores que 9 y menores que 17
- En otras palabras, los números presentes excluyen el cuadrado perfecto actual hasta incluir el siguiente cuadrado perfecto .
- Para encontrar la ‘L invertida’ en la que se encuentra el número, encuentra el techo de la raíz cuadrada del número
- Se calcula la diferencia entre el cuadrado de ‘L invertida’ y el número dado, digamos d
- Si l es la ‘L invertida’ en la que se encuentra el número y n denota el número dado, entonces:
re = l^2 – norte
- Si esta diferencia d es menor que n , entonces la fila r y la columna c de n vienen dadas por:
r = l
c = re + l
- Si esta diferencia d es mayor o igual que n , entonces la fila r y la columna c de n vienen dadas por:
r = 2l – re – 1
c = l
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ Implementation for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to find the coordinates of n
void findCoordinates(int n)
{
// Store the row and column of
// n respectively
int r, c;
// Stores the inverted L
// in which n lies
int l = ceil(sqrt(n));
// Stores the difference between
// square of l and n
int d = (l * l) - n;
// If d is less than l
if (d < l) {
r = l;
c = d + 1;
}
else {
c = l;
r = (2 * l) - d - 1;
}
cout << r << " " << c;
}
// Driver code
int main()
{
// Given n
int N = 10549857;
// Function call
findCoordinates(N);
return 0;
}
Java
// Java Implementation for the above approach
public class GFG {
// Function to find the coordinates of n
static void findCoordinates(int n)
{
// Store the row and column of
// n respectively
int r, c;
// Stores the inverted L
// in which n lies
int l = (int)Math.ceil(Math.sqrt(n));
// Stores the difference between
// square of l and n
int d = (l * l) - n;
// If d is less than l
if (d < l) {
r = l;
c = d + 1;
}
else {
c = l;
r = (2 * l) - d - 1;
}
System.out.print(r + " " + c);
}
// Driver code
public static void main (String[] args) {
// Given n
int N = 10549857;
// Function call
findCoordinates(N);
}
}
// This code is contributed by AnkThon
Python3
# Python Program to implement
# the above approach
import math
# Function to find the coordinates of n
def findCoordinates(n):
# Store the row and column of
# n respectively
#let r, c
# Stores the inverted L
# in which n lies
l = math.ceil(math.sqrt(n))
# Stores the difference between
# square of l and n
d = (l * l) - n
# If d is less than l
if (d < l):
r = l
c = d + 1
else:
c = l
r = (2 * l) - d - 1
print(f"{r} {c}")
# Driver code
# Given n
N = 10549857
# Function call
findCoordinates(N)
# This code is contributed by Saurabh Jaiswal
C#
// C# Implementation for the above approach
using System;
public class GFG {
// Function to find the coordinates of n
static void findCoordinates(int n)
{
// Store the row and column of
// n respectively
int r, c;
// Stores the inverted L
// in which n lies
int l = (int)Math.Ceiling(Math.Sqrt(n));
// Stores the difference between
// square of l and n
int d = (l * l) - n;
// If d is less than l
if (d < l) {
r = l;
c = d + 1;
}
else {
c = l;
r = (2 * l) - d - 1;
}
Console.Write(r + " " + c);
}
// Driver code
public static void Main (string[] args) {
// Given n
int N = 10549857;
// Function call
findCoordinates(N);
}
}
// This code is contributed by shivanisinghss2110
Javascript
<script>
// JavaScript Program to implement
// the above approach
// Function to find the coordinates of n
function findCoordinates(n) {
// Store the row and column of
// n respectively
let r, c;
// Stores the inverted L
// in which n lies
let l = Math.ceil(Math.sqrt(n));
// Stores the difference between
// square of l and n
let d = (l * l) - n;
// If d is less than l
if (d < l) {
r = l;
c = d + 1;
}
else {
c = l;
r = (2 * l) - d - 1;
}
document.write(r + " " + c);
}
// Driver code
// Given n
let N = 10549857;
// Function call
findCoordinates(N);
// This code is contributed by Potta Lokesh
</script>
353 3249
Tiempo Complejidad: O(1)
Espacio Auxiliar: O(1)
Publicación traducida automáticamente
Artículo escrito por anusha00466 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA