Suma máxima de distancias de un Node a todos los demás Nodes

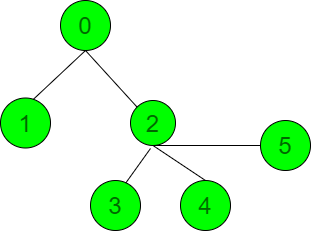
Dado un árbol conectado no dirigido con N Nodes valorados de 0 a N – 1 y una array bordes[][2] representa los bordes entre dos Nodes, la tarea es encontrar la suma máxima de distancias de un Node a cualquier otro Node en el árbol.

Ejemplos:

Entrada: N = 5, aristas = { {0, 2}, {1, 3}, {0, 1}, {3, 4} }

Salida: 10
Explicación:
considerando el Node 2 como el Node de origen, las distancias de todos los demás Nodes desde el Node 2 son: 1 (Node 0), 2 (Node 1), 3 (Node 3), 4 (Node 4). Por tanto, la suma de las distancias es 1 + 2 + 3 + 4 = 10.

Entrada: N = 6, bordes[][] = {{0, 1}, {0, 2}, {2, 3}, {2, 4}, {2, 5}}

Salida: 12

Enfoque ingenuo: el enfoque más simple para resolver el problema dado es realizar el recorrido de búsqueda en profundidad primero desde cada Node y encontrar la suma de la distancia cada dos Nodes desde el Node de origen actual. Después de verificar de todos los Nodes como el Node de origen, imprima la suma máxima entre todas las sumas de valores obtenidos.

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to perform DFS and find the
// distance from a node to every other
// node
void dfs(int s, vector<vector<int> > g,
         int p, int d, int& ans)
{
    for (int i : g[s]) {
 
        // If i is not equal to
        // parent p
        if (i != p) {
            ans += d;
            dfs(i, g, s, d + 1, ans);
        }
    }
}
 
// Function to find the maximum sum of
// distance from a node to every other
// node
void maxPotentialDistance(
    int N, vector<vector<int> >& edges)
{
    int ans = 0;
 
    // Construct the graph
    vector<vector<int> > g(N, vector<int>());
 
    for (auto& it : edges) {
        g[it[0]].push_back(it[1]);
        g[it[1]].push_back(it[0]);
    }
 
    // Find the sum of distances from
    // every node
    for (int i = 0; i < N; i++) {
 
        // Stores the maximum sum of
        // distance considering the
        // current node as source node
        int a = 0;
 
        // Perform DFS Traversal to
        // find the sum of distances
        dfs(i, g, -1, 1, a);
 
        // Update the maximum sum
        ans = max(ans, a);
    }
 
    // Print the maximum sum
    cout << ans;
}
 
// Driver Code
int main()
{
    int N = 6;
    vector<vector<int> > edges = {
        { 0, 1 }, { 0, 2 }, { 2, 3 }, { 2, 4 }, { 2, 5 }
    };
 
    maxPotentialDistance(N, edges);
 
    return 0;
}

# python program for the above approach
 
pd_0 = 0
 
# Function to perform DFS and find the
# distance from a node to every other
# node
 
 
def dfs(s, g, p, d, count):
    global pd_0
    for i in g[s]:
 
                # If i is not equal to
                # parent p
        if (i != p):
            pd_0 += d
 
            # Perform the DFS Traversal
            dfs(i, g, s, d + 1, count)
 
            # Update the count of
            # nodes
            count[s] = count[s] + count[i]
 
 
# Function to find the distances from
# every other node using distance from
# node 0
def dfs2(s, g, p, pd_all, n, count):
 
    for i in g[s]:
 
                # If i is not equal to the
                # parent p
        if (i != p):
            pd_all[i] = pd_all[s] - count[i] + n - count[i]
            dfs2(i, g, s, pd_all, n, count)
 
 
# Function to find the maximum sum of
# distance from a node to every other
# node
def maxPotentialDistance(N, edges):
    global pd_0
    ans = 0
 
    # Construct the graph
    g = [[] for _ in range(N)]
 
    for it in edges:
        g[it[0]].append(it[1])
        g[it[1]].append(it[0])
 
        # Stores the number of nodes in
        # each subtree
 
    count = [1 for _ in range(N)]
 
    # Find the sum of distances from
    # node 0 and count the number of
    # nodes in each subtree
 
    dfs(0, g, -1, 1, count)
 
    # Stores distances from each node
    pd_all = [0 for _ in range(N)]
    pd_all[0] = pd_0
 
    # Find the distances from each
    # node using distance from node 0
 
    dfs2(0, g, -1, pd_all, N, count)
 
    # Find the result
 
    for i in pd_all:
        ans = max(ans, i)
 
        # Print the result
    print(ans)
 
 
# Driver Code
if __name__ == "__main__":
 
    N = 6
    edges = [
            [0, 1], [0, 2], [2, 3], [2, 4], [2, 5]
    ]
    maxPotentialDistance(N, edges)
 
    # This code is contributed by rakeshsahni

// C# program to implement above approach
using System;
using System.Collections.Generic;
 
class GFG
{
 
  // Stores the maximum sum of
  // distance considering the
  // current node as source node
  public static int temp_ans = 0;
 
  // Function to perform DFS and find the
  // distance from a node to every other
  // node
  public static void dfs(int s, List<List<int>> g, int p, int d)
  {
    foreach (int i in g[s]) {
 
      // If i is not equal to
      // parent p
      if (i != p) {
        temp_ans += d;
        dfs(i, g, s, d + 1);
      }
    }
  }
 
  // Function to find the maximum sum of
  // distance from a node to every other
  // node
  public static void maxPotentialDistance(int N, List<List<int>> edges)
  {
    int ans = 0;
 
    // Construct the graph
    List<List<int> > g = new List<List<int>>();
    for(int i = 0 ; i < N ; i++){
      g.Add(new List<int>());
    }
 
    foreach (List<int> it in edges) {
      g[it[0]].Add(it[1]);
      g[it[1]].Add(it[0]);
    }
 
    // Find the sum of distances from
    // every node
    for (int i = 0; i < N; i++) {
 
 
      // Perform DFS Traversal to
      // find the sum of distances
      dfs(i, g, -1, 1);
 
      // Update the maximum sum
      ans = Math.Max(ans, temp_ans);
      temp_ans = 0;
    }
 
    // Print the maximum sum
    Console.Write(ans);
  }
 
 
 
  // Driver Code
  public static void Main(string[] args){
 
    int N = 6;
    List<List<int>> edges = new List<List<int>>{
      new List<int>{ 0, 1 },
      new List<int>{ 0, 2 },
      new List<int>{ 2, 3 },
      new List<int>{ 2, 4 },
      new List<int>{ 2, 5 }
    };
 
    maxPotentialDistance(N, edges);
 
  }
}
 
// This code is contributed by subhamgoyal2014.

12

Tiempo Complejidad: O(N ² )
Espacio Auxiliar: O(N)

Enfoque eficiente: el enfoque anterior también se puede optimizar observando que existe una relación entre la suma de las distancias de los Nodes a todos los demás Nodes. Tomemos el Node x . Si y es su hijo, entonces se observa que la suma de las distancias de yyx están relacionadas como;
 

distancia de y = distancia x – número de Nodes en el subárbol y + Nodes que no están en el subárbol y

Las distancias requeridas de todos los Nodes se pueden calcular calculando la suma de las distancias desde un Node y conociendo el número de Nodes en cada subárbol. Siga los pasos a continuación para resolver el problema:

• Defina una función dfs(int s, vector<vector<int> > graph, int p, int d, int &ans, vector<int>&count) y realice los siguientes pasos:
  • Itere sobre el rango [0, graph[s]] usando la variable i y si i no es igual a p, entonces aumente el valor de ans por d y llame a la función dfs(i, graph, s, d + 1, ans , count) para explorar otros Nodes y establecer el valor de count[s] como (count[s] + count[i]) .
• Defina una función dfs2(int s, vector<vector<int> > graph, int p, vector<int> &pd_all, int N, vector<int>&count) y realice los siguientes pasos:
  • Itere sobre el rango [0, graph[s]] usando la variable i y si i no es igual a p, entonces establezca el valor de pd_all[i] como (pd_all[s] – count[i] + n – count[ i]) y llame a la función dfs(i, graph, s, pd_all, N, count)  para encontrar la respuesta para otros Nodes.
• Inicialice la variable, digamos ans que almacena el resultado.
• Construya una lista de adyacencia, grafique[] a partir de los bordes[][] dados .
• Inicialice el vector count[] de tamaño N para realizar un seguimiento del recuento de Nodes en el subárbol de un Node determinado.
• Inicialice la variable pd_0 como 0 para almacenar la suma de las distancias desde el Node 0 hasta todos los demás Nodes del árbol.
• Llame a la función dfs(s, graph, p, d, ans, count) para encontrar la distancia requerida desde el Node 0 hasta cualquier otro Node y almacene el conteo del número de Nodes en un subárbol.
• Inicialice el vector pd_all[] de tamaño N para almacenar las distancias desde cualquier otro Node.
• Establezca el valor de pd_all[0] como pd_0 .
• Llame a la función dfs2(s, graph, p, pd_all, N, count) para encontrar las distancias requeridas desde cualquier otro Node.
• Itere sobre el rango [0, N] usando la variable i y actualice el valor de ans como el máximo de ans o pd_all[i] .
• Después de realizar los pasos anteriores, imprima el valor de ans como respuesta.

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
 
// Function to perform DFS and find the
// distance from a node to every other
// node
void dfs(int s, vector<vector<int> > g,
         int p, int d, int& ans,
         vector<int>& count)
{
    for (int i : g[s]) {
 
        // If i is not equal to
        // parent p
        if (i != p) {
            ans += d;
 
            // Perform the DFS Traversal
            dfs(i, g, s, d + 1,
                ans, count);
 
            // Update the count of
            // nodes
            count[s] = count[s] + count[i];
        }
    }
}
 
// Function to find the distances from
// every other node using distance from
// node 0
void dfs2(int s, vector<vector<int> > g,
          int p, vector<int>& pd_all,
          int n, vector<int> count)
{
    for (int i : g[s]) {
 
        // If i is not equal to the
        // parent p
        if (i != p) {
            pd_all[i] = pd_all[s]
                        - count[i]
                        + n - count[i];
            dfs2(i, g, s, pd_all,
                 n, count);
        }
    }
}
 
// Function to find the maximum sum of
// distance from a node to every other
// node
void maxPotentialDistance(
    int N, vector<vector<int> >& edges)
{
    int ans = 0;
 
    // Construct the graph
    vector<vector<int> > g(N, vector<int>());
 
    for (auto& it : edges) {
        g[it[0]].push_back(it[1]);
        g[it[1]].push_back(it[0]);
    }
 
    // Stores the number of nodes in
    // each subtree
    vector<int> count(N, 1);
    int pd_0 = 0;
 
    // Find the sum of distances from
    // node 0 and count the number of
    // nodes in each subtree
    dfs(0, g, -1, 1, pd_0, count);
 
    // Stores distances from each node
    vector<int> pd_all(N, 0);
    pd_all[0] = pd_0;
 
    // Find the distances from each
    // node using distance from node 0
    dfs2(0, g, -1, pd_all, N, count);
 
    // Find the result
    for (int i : pd_all)
        ans = max(ans, i);
 
    // Print the result
    cout << ans;
}
 
// Driver Code
int main()
{
    int N = 6;
    vector<vector<int> > edges = {
        { 0, 1 }, { 0, 2 }, { 2, 3 }, { 2, 4 }, { 2, 5 }
    };
    maxPotentialDistance(N, edges);
 
    return 0;
}

12

Complejidad temporal: O(N)
Espacio auxiliar: O(N)