Circuito del puente de Wheatstone

El puente de Wheatstone se usa Para encontrar la resistencia de un conductor, en 1842, el científico Wheatstone propuso una teoría, que se llama el principio del puente de Wheatstone por su nombre. podemos probar o establecer la fórmula de Wheatstone usando las leyes de Kirchhoff. El puente de Wheatstone es simplemente un circuito eléctrico que se utiliza para medir una resistencia eléctrica desconocida equilibrando dos puntos de un puente. ¡Empecemos!

¿Qué es la ley de Kirchhoff?

En 1842, el científico Kirchhoff formuló dos leyes para encontrar la distribución de corriente en diferentes conductores en cualquier circuito eléctrico complejo. Estas reglas son las siguientes:

• Primera ley: La suma algebraica de todas las corrientes eléctricas que se encuentran en cada unión de un circuito eléctrico es cero. En términos matemáticos, en cualquier unión: ΣI = 0. Las corrientes que llegan a la unión se toman como positivas y las corrientes que se alejan de la unión se toman como negativas. En otras palabras, cuando fluye una corriente constante en un circuito, no se acumula ni se elimina carga de ninguna unión del circuito, es decir, la ley de Kirchhoff se basa en el principio de conservación de la carga. También se le llama ley de corriente de Kirchhoff .
• Segunda ley: En cualquier circuito eléctrico cerrado, la suma algebraica de los productos de las corrientes que fluyen en diferentes secciones y sus correspondientes resistencias (es decir, diferencia de potencial) y las diferentes fuerzas electroportadoras aplicadas en ese circuito es cero. En lenguaje matemático, ΣIR + ΣE = 0. La segunda ley de Kirchhoff es en realidad la ley de conservación de la energía, según la cual no debería haber cambio en su energía cuando una carga se mueve en un circuito completamente cerrado. También se le llama ley de voltaje de Kirchhoff .

Principio del puente de Wheatstone:

Según este principio, se colocan cuatro resistencias P, Q, R y S en forma de los cuatro lados AB, BC, AD y DC de un cuadrilátero ABCD. Se coloca una celda E y clave K ₁ , entre los extremos A y C de este cuadrilátero y un galvanómetro sensible G y clave K ₂ , se coloca entre los extremos B y D. Claramente, el potencial del punto A será igual al potencial de la placa positiva de la celda y el potencial del punto C será igual al potencial de la placa negativa de la celda.

Está claro a partir de la figura que las resistencias P y Q están en serie cuando la llave K ₂ está abierta. De manera similar, las resistencias R y S están en serie, pero P y Q juntas (brazo ABC) y R y S juntas (brazo ADC) están conectadas en paralelo entre sí. Como el lado BD del galvanómetro está colocado como un puente sobre los lados ABC y ADC del cuadrilátero, este circuito se llama puente.

Cuando el puente está en un estado de equilibrio, es decir, no hay deflexión en el galvanómetro. Es decir, en el estado de equilibrio del puente, la relación de las resistencias de cualesquiera dos brazos adyacentes es igual a la relación de los dos lados adyacentes restantes. 

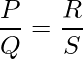
Establecimiento de fórmulas a partir de la ley de Kirchhoff:

Supongamos que, al pulsar la tecla K ₁ de la celda, fluye una corriente I a través de la celda, que se divide en dos partes en el extremo A. Una parte I ₁ fluye a través de la resistencia P en el brazo AB y la otra parte I ₂ , a través de la resistencia R en el brazo AD. La corriente I ₁ llega de nuevo al extremo B y se divide en dos partes. Una parte de ella I _g fluye a través del galvanómetro en el brazo BD y la parte restante (I ₁ – I _g ) fluye a través de la resistencia Q en el brazo BC. En el extremo D, la corriente I ₂ del brazo AD y la corriente Ig del brazo BD, por lo que la corriente que fluye a través de la resistencia S en el brazo DC será (I ₂ + I _g ).

Entonces, de acuerdo con la ley de Kirchhoff, en el camino cerrado ABDA,

yo ₁ PAG + yo _gramo G – yo ₂ R = 0                                                                                                                                                                            ……(1)

Y en camino cerrado BCDB, 

(yo ₁ – yo _gramo )Q – (yo ₂ – yo _gramo )S – yo _gramo G = 0                                                                                                                                                             ……(2)

Los valores de las resistencias P, Q, R y S se toman de tal forma que no circula corriente por el galvanómetro G cuando se pulsa la tecla K ₂ . A esto se le llama estado de equilibrio del puente , es decir, en el estado de equilibrio del puente, la deflexión en el galvanómetro es cero (I _g = 0).

Poniendo I _g = 0, en las ecuaciones anteriores,

yo ₁ P = yo ₂ R y yo ₁ Q = yo ₂ S

o 

Yo ₁ P / Yo ₁ Q = Yo ₂ R / Yo ₂ S

o 

P / Q = R / S                                                                  

Esta es la condición necesaria para el equilibrio del puente de Wheatstone. Con la ayuda de la fórmula anterior, conociendo los valores de tres resistencias P, Q y R, se puede encontrar el valor de la cuarta resistencia S.

Generalmente, los brazos con resistencia P y Q se denominan brazos de relación . El brazo AD con resistencia R se llama brazo conocido y el brazo CD con resistencia S se llama brazo desconocido . En la posición de equilibrio del puente, cambiar la posición de la celda y el galvanómetro no afecta el estado de equilibrio (en este caso el potencial de los puntos A y C será el mismo), por lo que los brazos AC y BD son brazos conjugados . son llamados. La sensibilidad del puente es más alta cuando las resistencias de los cuatro brazos son casi iguales.

Hay que recordar que en el estado de equilibrio (cuando P / Q = R / S), la resistencia total del circuito entre los puntos A y C será igual a (P + Q) × (R + S) / (P + Q) + (R + S) [porque la resistencia del brazo ABC es (P + Q) y la resistencia del brazo ADC (R + S) están conectadas en orden paralelo] y los potenciales de los puntos B y D serán los mismos.

Está claro que si el potencial del punto B es mayor que el potencial del punto D, al presionar la tecla K ₂ del galvanómetro , la corriente comenzará a fluir del punto B al D, lo que desviará el galvanómetro hacia un lado. Por el contrario, si el potencial en el punto D es mayor que el potencial en el punto B, la corriente fluirá del punto D al B cuando se presione la tecla K2 del galvanómetro, lo que hará _que el galvanómetro se desvíe en la dirección opuesta.

Ventajas del Puente de Wheatstone:

• Con la ayuda del Puente de Wheatstone, podemos construir un puente de Metro.
• La mayor ventaja del puente de Wheatstone es medir con precisión la resistencia eléctrica en lugar de utilizar instrumentos costosos.
• Podemos medir cambios diminutos en el puente, incluso en m ohmios.
• Es muy fácil averiguar la resistencia desconocida ya que el resto de las tres se conocen fácilmente.
• Podemos medir la tensión y la presión usando un puente de Wheatstone.

Desventajas del puente de Wheatstone:

• El resultado del puente de Wheatstone puede verse fácilmente afectado por la temperatura y las células EMF.
• El puente de Wheatstone también puede verse afectado si el galvanómetro no es de buena calidad.
• El puente de Wheatstone falla si no está en condiciones de equilibrio.
• No podemos medir una gran resistencia con la ayuda del Puente de Wheatstone. 
• El costo de mantenimiento del Puente de Wheatstone es muy alto.

El puente del medidor se muestra en la figura. Está hecho de un alambre de un metro de largo con un área de sección transversal uniforme que se sujeta verticalmente entre dos placas gruesas de metal, como se muestra en la figura. Hay dos espacios en la placa metálica entre los cuales se pueden conectar resistencias. Los puntos finales donde se sujetan los cables están conectados a la celda mediante una llave. Un extremo del galvanómetro está conectado a una placa metálica en el medio del espacio. El otro extremo del galvanómetro está conectado al jockey. Un jockey es esencialmente una varilla metálica con un borde afilado en un extremo y que puede deslizarse sobre un cable para formar una conexión eléctrica. R es una resistencia desconocida cuyo valor deseamos encontrar. Combínalo en cualquiera de los espacios. Una resistencia estándar conocida S está conectada entre el segundo espacio.

Toque un punto D en el cable del jockey que esté a una distancia de 1 cm del extremo A. Puede deslizar el jockey a lo largo del cable. La resistencia de la parte AD del alambre es R _cm l donde R _cm es la resistencia por unidad cm del alambre. Por tanto, la resistencia de la parte de CC es R _cm ( 100 – l ).

Cuatro brazos AB, BC, DA y CD [cuyas resistencias son R, S, R _cm l y R _cm (100 – l) respectivamente] obviamente forman un puente de Wheatstone con el brazo de la batería de CA y el brazo del galvanómetro BD. Si el jockey se mueve a lo largo del cable, llegará un punto (punto de equilibrio) donde el galvanómetro no mostrará ninguna corriente. Sea la distancia del jockey en el punto de equilibrio = 1, entonces los valores de las cuatro resistencias del puente en el punto de equilibrio son R, S, R _cm l1 y R _cm (100 – l1). Según la Ecuación Puente de Wheatstone para la condición de equilibrio.

R / S = R _cm l ₁ / (R _cm (100 – l ₁ ) 

          = l ₁ / 100 – l ₁

Tan pronto como encontramos el valor de l1, la resistencia desconocida R se obtiene en términos de la resistencia estándar conocida S. por lo tanto:

R = S ( l ₁ / 100 – l ₁ )

Al elegir diferentes valores de S, obtenemos diferentes valores de l ₁ y calculamos R cada vez. Por supuesto, un error en la medición de l ₁ dará como resultado un error en R. Se puede demostrar que el porcentaje de error en R se puede minimizar ajustando el punto de equilibrio colocando l ₁ más cerca de la mitad del cable del puente, 50 cm (esto requiere una elección adecuada de S).

Ejemplos de preguntas 

Pregunta 1: Encuentre la resistencia equivalente entre los puntos A y C en el circuito que se muestra en la siguiente figura:

Responder: 

El circuito equivalente del circuito que se muestra en la figura anterior se da como:

Ya que, 

2/3 = 4/6, este es el circuito de un puente de Wheatstone balanceado.  

En el estado equilibrado, VB = VD, por lo que no fluirá corriente a través de la resistencia de 5 Ω.  

Ahora la resistencia equivalente de los lados AB y BC es R’ = 2 + 3 = 5 Ω.  

La resistencia equivalente del brazo AD y DC R” = 4 + 6 = 10 Ω 

Si la resistencia equivalente entre los puntos A y C es R, entonces. 

1/R = (1/R’) + (1/R”)

o

1 / R = (1 / 5) + (1 / 10)

        = 1 / R = (2 + 1) / 10

o 

R = 10 / 3 

   = 3,33 Ω

Pregunta 3: El circuito eléctrico de un puente de Wheatstone equilibrado se muestra en la figura. Calcular la resistencia x.

Responder: 

Sea R la resistencia total en el brazo BC. Dado que el puente está equilibrado, entonces:

15 / R = 5 / 10 

R = (15 × 10) / 5 = 3 Ω 

1 / R = (1 / X) + (1 / 60)

o                                                                                                                    

1 / 30 = (1 / X) + (1 / 60)

o 

1 / X = 1 / 30 – 1 / 60

1 / X = 2 – 1 / 60 = 1 / 60

o

X = 60 Ω 

Pregunta 4: ¿Qué es Meter Bridge? ¿Y qué tipo de precauciones necesitamos para realizar mediciones usando Meter Bridge?

Responder: 

Un puente Meter es un dispositivo basado en el principio del puente de Wheatstone, con la ayuda del cual se puede determinar la resistencia y la resistencia específica de un conductor. En este, un alambre de 1 metro de largo actúa como el lado proporcional.

Precauciones durante el uso de Meter Bridge: Las precauciones son: 

1. Los extremos de todos los cables de conexión deben limpiarse con papel de lija.  
2. La corriente no debe fluir en el circuito durante mucho tiempo, de lo contrario, su resistencia aumenta debido al calentamiento del cable del puente. Por lo tanto, la llave en el circuito de la celda debe enchufarse solo cuando se van a realizar observaciones.  
3. No se debe hacer funcionar el jockey frotándolo en el cable del puente del medidor, de lo contrario, el grosor del cable no permanecerá igual en todos los lugares.  
4. Inicialmente se debe usar una derivación con un galvanómetro durante el ajuste, pero la derivación debe retirarse cerca de la posición de deflexión cero.  
5. Solo se debe quitar un enchufe de resistencia de este tipo de la caja de resistencia para que la posición de deflexión cero esté aproximadamente en el medio del cable del puente. En este caso, la sensibilidad del puente es máxima y el porcentaje de error es mínimo.  
6. Todos los demás enchufes en la caja de resistencia, excepto aquellos que se hayan quitado, deben estar apretados. 

Pregunta 5: En la siguiente figura, ¿la corriente a través de la resistencia de 4Ω es?

Responder: 

Ya que, Q/P = S/R  

⇒ 4 / 20 = 10 / 50 

Es un ejemplo de puente de trigo-piedra equilibrado.

Por lo tanto, no fluirá corriente a través de una resistencia de 16 Ω.

Como sabemos que la corriente se divide en razón inversa, la corriente a través de la resistencia de 4Ω es,

= 1,4 × (20+4)+(50+10) / (50+10) 

= 1,4 × (7/5) 

= 1 A