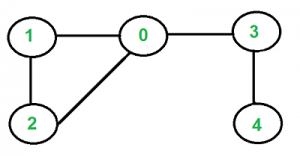
Dado un gráfico no dirigido, ¿cómo verificar si hay un ciclo en el gráfico? Por ejemplo, el siguiente gráfico tiene un ciclo 1-0-2-1.
Hemos discutido la detección de ciclos para el gráfico dirigido . También hemos discutido un algoritmo de búsqueda de unión para la detección de ciclos en gráficos no dirigidos. . La complejidad temporal del algoritmo de búsqueda de unión es O(ELogV). Al igual que los gráficos dirigidos, podemos usar DFS para detectar un ciclo en un gráfico no dirigido en tiempo O(V+E). Hemos discutido la solución basada en DFS para la detección de ciclos en un gráfico no dirigido .
En este artículo, el BFSSe discute la solución basada. Hacemos un recorrido BFS del gráfico dado. Para cada vértice visitado ‘v’, si hay una ‘u’ adyacente tal que u ya fue visitada y u no es un padre de v, entonces hay un ciclo en el gráfico. Si no encontramos tal adyacente para ningún vértice, decimos que no hay ciclo.
Usamos una array principal para realizar un seguimiento del vértice principal de un vértice para que no consideremos el padre visitado como un ciclo.
C++
// C++ program to detect cycle
// in an undirected graph
// using BFS.
#include <bits/stdc++.h>
using namespace std;
void addEdge(vector<int> adj[], int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
bool isCyclicConntected(vector<int> adj[], int s,
int V, vector<bool>& visited)
{
// Set parent vertex for every vertex as -1.
vector<int> parent(V, -1);
// Create a queue for BFS
queue<int> q;
// Mark the current node as
// visited and enqueue it
visited[s] = true;
q.push(s);
while (!q.empty()) {
// Dequeue a vertex from queue and print it
int u = q.front();
q.pop();
// Get all adjacent vertices of the dequeued
// vertex u. If a adjacent has not been visited,
// then mark it visited and enqueue it. We also
// mark parent so that parent is not considered
// for cycle.
for (auto v : adj[u]) {
if (!visited[v]) {
visited[v] = true;
q.push(v);
parent[v] = u;
}
else if (parent[u] != v)
return true;
}
}
return false;
}
bool isCyclicDisconntected(vector<int> adj[], int V)
{
// Mark all the vertices as not visited
vector<bool> visited(V, false);
for (int i = 0; i < V; i++)
if (!visited[i] && isCyclicConntected(adj, i,
V, visited))
return true;
return false;
}
// Driver program to test methods of graph class
int main()
{
int V = 4;
vector<int> adj[V];
addEdge(adj, 0, 1);
addEdge(adj, 1, 2);
addEdge(adj, 2, 0);
addEdge(adj, 2, 3);
if (isCyclicDisconntected(adj, V))
cout << "Yes";
else
cout << "No";
return 0;
}
Java
// Java program to detect cycle in
// an undirected graph using BFS.
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
class cycle
{
public static void main(String arg[])
{
int V = 4;
@SuppressWarnings("unchecked")
ArrayList <Integer> adj[] = new ArrayList[V];
for(int i = 0; i < 4; i++)
adj[i] = new ArrayList<Integer>();
addEdge(adj, 0, 1);
addEdge(adj, 1, 2);
addEdge(adj, 2, 0);
addEdge(adj, 2, 3);
if (isCyclicDisconntected(adj, V))
System.out.println("Yes");
else
System.out.println("No");
}
static void addEdge(ArrayList<Integer> adj[], int u, int v)
{
adj[u].add(v);
adj[v].add(u);
}
static boolean isCyclicConntected(
ArrayList<Integer> adj[], int s,
int V, boolean visited[])
{
// Set parent vertex for every vertex as -1.
int parent[] = new int[V];
Arrays.fill(parent, -1);
// Create a queue for BFS
Queue<Integer> q = new LinkedList<>();
// Mark the current node as
// visited and enqueue it
visited[s] = true;
q.add(s);
while (!q.isEmpty())
{
// Dequeue a vertex from
// queue and print it
int u = q.poll();
// Get all adjacent vertices
// of the dequeued vertex u.
// If a adjacent has not been
// visited, then mark it visited
// and enqueue it. We also mark parent
// so that parent is not considered
// for cycle.
for (int i = 0; i < adj[u].size(); i++)
{
int v = adj[u].get(i);
if (!visited[v])
{
visited[v] = true;
q.add(v);
parent[v] = u;
}
else if (parent[u] != v)
return true;
}
}
return false;
}
static boolean isCyclicDisconntected(
ArrayList<Integer> adj[], int V)
{
// Mark all the vertices as not visited
boolean visited[] = new boolean[V];
Arrays.fill(visited,false);
for (int i = 0; i < V; i++)
if (!visited[i] &&
isCyclicConntected(adj, i, V, visited))
return true;
return false;
}
}
// This code is contributed by mayukh Sengupta
Python3
# Python3 program to detect cycle in
# an undirected graph using BFS.
from collections import deque
def addEdge(adj: list, u, v):
adj[u].append(v)
adj[v].append(u)
def isCyclicConnected(adj: list, s, V,
visited: list):
# Set parent vertex for every vertex as -1.
parent = [-1] * V
# Create a queue for BFS
q = deque()
# Mark the current node as
# visited and enqueue it
visited[s] = True
q.append(s)
while q != []:
# Dequeue a vertex from queue and print it
u = q.pop()
# Get all adjacent vertices of the dequeued
# vertex u. If a adjacent has not been visited,
# then mark it visited and enqueue it. We also
# mark parent so that parent is not considered
# for cycle.
for v in adj[u]:
if not visited[v]:
visited[v] = True
q.append(v)
parent[v] = u
elif parent[u] != v:
return True
return False
def isCyclicDisconnected(adj: list, V):
# Mark all the vertices as not visited
visited = [False] * V
for i in range(V):
if not visited[i] and \
isCyclicConnected(adj, i, V, visited):
return True
return False
# Driver Code
if __name__ == "__main__":
V = 4
adj = [[] for i in range(V)]
addEdge(adj, 0, 1)
addEdge(adj, 1, 2)
addEdge(adj, 2, 0)
addEdge(adj, 2, 3)
if isCyclicDisconnected(adj, V):
print("Yes")
else:
print("No")
# This code is contributed by
# sanjeev2552
C#
// A C# program to detect cycle in
// an undirected graph using BFS.
using System;
using System.Collections.Generic;
class GFG
{
public static void Main(String []arg)
{
int V = 4;
List<int> []adj = new List<int>[V];
for (int i = 0; i < 4; i++)
{
adj[i] = new List<int>();
}
addEdge(adj, 0, 1);
addEdge(adj, 1, 2);
addEdge(adj, 2, 0);
addEdge(adj, 2, 3);
if (isCyclicDisconntected(adj, V))
{
Console.WriteLine("Yes");
}
else
{
Console.WriteLine("No");
}
}
static void addEdge(List<int> []adj, int u, int v)
{
adj[u].Add(v);
adj[v].Add(u);
}
static bool isCyclicConntected(List<int> []adj, int s,
int V, bool []visited)
{
// Set parent vertex for every vertex as -1.
int []parent = new int[V];
for (int i = 0; i < V; i++)
parent[i] = -1;
// Create a queue for BFS
Queue<int> q = new Queue<int>();
// Mark the current node as
// visited and enqueue it
visited[s] = true;
q.Enqueue(s);
while (q.Count != 0)
{
// Dequeue a vertex from
// queue and print it
int u = q.Dequeue();
// Get all adjacent vertices
// of the dequeued vertex u.
// If a adjacent has not been
// visited, then mark it visited
// and enqueue it. We also mark parent
// so that parent is not considered
// for cycle.
for (int i = 0; i < adj[u].Count; i++)
{
int v = adj[u][i];
if (!visited[v])
{
visited[v] = true;
q.Enqueue(v);
parent[v] = u;
}
else if (parent[u] != v)
{
return true;
}
}
}
return false;
}
static bool isCyclicDisconntected(List<int> []adj, int V)
{
// Mark all the vertices as not visited
bool []visited = new bool[V];
for (int i = 0; i < V; i++)
{
if (!visited[i] &&
isCyclicConntected(adj, i, V, visited))
{
return true;
}
}
return false;
}
}
// This code is contributed by PrinciRaj1992
Javascript
<script>
// A JavaScript program to detect cycle in
// an undirected graph using BFS.
var V = 4;
var adj = Array.from(Array(V), ()=>Array());
addEdge(adj, 0, 1);
addEdge(adj, 1, 2);
addEdge(adj, 2, 0);
addEdge(adj, 2, 3);
if (isCyclicDisconntected(adj, V))
{
document.write("Yes");
}
else
{
document.write("No");
}
function addEdge(adj, u, v)
{
adj[u].push(v);
adj[v].push(u);
}
function isCyclicConntected(adj, s, V, visited)
{
// Set parent vertex for every vertex as -1.
var parent = Array(V).fill(-1);
// Create a queue for BFS
var q = [];
// Mark the current node as
// visited and enqueue it
visited[s] = true;
q.push(s);
while (q.length != 0)
{
// Dequeue a vertex from
// queue and print it
var u = q.shift();
// Get all adjacent vertices
// of the dequeued vertex u.
// If a adjacent has not been
// visited, then mark it visited
// and enqueue it. We also mark parent
// so that parent is not considered
// for cycle.
for (var i = 0; i < adj[u].length; i++)
{
var v = adj[u][i];
if (!visited[v])
{
visited[v] = true;
q.push(v);
parent[v] = u;
}
else if (parent[u] != v)
{
return true;
}
}
}
return false;
}
function isCyclicDisconntected(adj, V)
{
// Mark all the vertices as not visited
var visited = Array(V).fill(false);
for (var i = 0; i < V; i++)
{
if (!visited[i] &&
isCyclicConntected(adj, i, V, visited))
{
return true;
}
}
return false;
}
</script>
Producción:
Yes
Complejidad de tiempo: el programa realiza un recorrido BFS simple de gráfico y el gráfico se representa mediante una lista de adyacencia. Entonces la complejidad del tiempo es O(V+E)