En probabilidad y estadística, la distribución t de Student (o simplemente la distribución t) es cualquier miembro de una familia de distribuciones de probabilidad continuas. Viene a la imagen al estimar la media de una población distribuida normalmente, donde el tamaño de la muestra es pequeño y la desviación estándar (SD) es indefinida y desconocida. La distribución t con gl = n grados de libertad tiene densidad
![]()
Si una variable aleatoria X tiene una distribución T con ν grados de libertad, entonces Pr (X ≤ x) = P. Suponga que Z e Y son variables aleatorias independientes. Sea Z una variable aleatoria normal estándar (media de 0, la varianza de 1). Y Y una variable chi-cuadrado con m grados de libertad. Ahora tenemos,
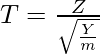
La variable T tiene la distribución t con m grados de libertad.
Método 1: Usar el método tinv()
PEIP es un paquete en R que se usa para aplicar muchas traducciones y cálculos de MATLAB en R. Es útil para estadísticas de datos y operaciones matemáticas. Este método es más preciso en comparación con el método qt(). El paquete se puede instalar en el espacio de trabajo usando el siguiente comando:
install.packages("PEIP")
El método tinv() de este paquete se basa en la función betaincinv. Se utiliza para calcular la distribución t inversa. Devuelve el quintil para la distribución T. Un valor p es una probabilidad de que los resultados de sus datos de muestra se hayan producido por casualidad.
Sintaxis: tinv(p, nu)
Argumentos:
- p : valor p
- nu : grados de libertad
El siguiente fragmento de código ilustra el cálculo de la distribución t inversa considerando la probabilidad aleatoria de un número 0.4 (valor p) con 2 grados de libertad:
R
# loading the required library
library("PEIP")
# defining p-value
p <- 0.4
nu <- 2
print ("Inverse t-distribution")
tinv(p, nu)
Producción:
[1] "Inverse t-distribution" [1] -0.2887
Método 2: Usar el método qt()
El método qt() en base R se utiliza para devolver la densidad acumulada de probabilidad inversa de la distribución t de Student, también conocida como distribución T. Es básicamente una función cuantil.
Sintaxis: qt(p, nu )
Argumentos:
- p : vector de probabilidades.
- nu : grados de libertad
El siguiente fragmento de código ilustra el cálculo de la distribución t inversa considerando la probabilidad aleatoria de un pequeño número exponencial 1e-20 (valor p) con 2 grados de libertad. El signo negativo ilustra que está declinando en la naturaleza mucho hacia el -ve NaN:
R
# defining p-value
p <- 1e-20
nu <- 2
print ("Inverse t-distribution")
qt(p, nu)
Producción:
[1] "Inverse t-distribution" [1] -7071067812
Se toma un vector de valores x en forma de secuencia, considerando que el número de grados de libertad es 15. Los valores y correspondientes se pueden calcular usando el método qt() en R. El siguiente fragmento de código ilustra el uso de este método sobre un vector de valores:
R
# creating a vec
x <- seq(.1, .9, by = .1)
# Calling qt() Function
y <- qt(x, 15)
print ("inverse t-distribution")
print (y)
# plotting data
plot (x, y, type = "o")
Producción:
[1] “distribución t inversa”
[1] -1,3406056 -0,8662450 -0,5357291 -0,2578853 0,0000000 0,2578853 0,5357291 0,8662450 1,3406056
