Introducción al análisis de potencia en Python

Para entender qué es el análisis de potencia, primero debemos echar un vistazo a los conceptos de una prueba de hipótesis estadística. Una prueba de hipótesis estadística calcula alguna cantidad bajo un supuesto dado (hipótesis nula) y el resultado de la prueba nos permite interpretar si el supuesto es válido o si se ha violado. Una violación de la suposición de la prueba a menudo se denomina primera hipótesis o hipótesis alternativa. El valor p y los valores críticos son los resultados más comunes de una prueba estadística que pueden interpretarse de diferentes maneras.  

El valor p se compara con el nivel de significación   (especificado antes del experimento, y su valor depende del tipo de experimento y los requisitos comerciales). Las medidas típicas del nivel de significación son 0,10 o 10 %, 0,05 o 5 % y 0,01 o 1 %.

• Si p-value <= 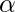 : Rechazar la hipótesis nula (resultado significativo).
• Si p-value > 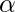 : No se puede rechazar la hipótesis nula (resultado no significativo).

Todas las pruebas de hipótesis estadísticas tienen la posibilidad de cometer cualquiera de los siguientes tipos de errores:

• Error Tipo I: Rechazo incorrecto de una hipótesis nula verdadera o un falso positivo .
• Error Tipo II: Aceptación incorrecta de una hipótesis nula falsa o de un negativo falso .

Poder estadístico: Solo es relevante cuando la hipótesis nula es falsa. El poder estadístico de una prueba de hipótesis es la probabilidad de rechazar correctamente una hipótesis nula o la posibilidad de aceptar la hipótesis alternativa si es verdadera. Por lo tanto, cuanto mayor sea el poder estadístico para una prueba determinada, menor será la probabilidad de cometer un error de tipo II (falso negativo). 

El último concepto que debe tener en cuenta antes de proceder al análisis de poder estadístico es el tamaño del efecto . Es la magnitud cuantificada de un resultado o efecto presente en una población de un experimento, generalmente medida por una medida estadística específica como la correlación de Pearson o la d de Cohen para la diferencia en las medias de dos grupos. Los tamaños del efecto pequeño, mediano, grande y muy grande comúnmente aceptados para la d de Cohen son 0,20, 0,50, 0,80 y 1,3, respectivamente. El tamaño del efecto o «efecto esperado» se determina a partir de estudios piloto, hallazgos de estudios similares, efecto definido en el campo o una conjetura fundamentada.

Análisis de potencia:Se construye a partir de 4 variables, a saber, Tamaño del efecto, Nivel de significación, Potencia, Tamaño de la muestra. Todas estas variables están interrelacionadas en el sentido de que cambiar una de ellas impacta en las otras tres. Siguiendo esta relación, el análisis de potencia implica determinar la cuarta variable cuando se conocen las otras tres variables. Es una poderosa herramienta para el diseño experimental. Por ejemplo, antes de un experimento, el tamaño de la muestra necesario para detectar un efecto particular se puede estimar dados los diferentes niveles deseados de significación, tamaño del efecto y poder. Alternativamente, los hallazgos de un estudio pueden ser validados. El poder estadístico se puede determinar utilizando el tamaño de la muestra, el tamaño del efecto y el nivel de significación dados, lo que ayuda a concluir si la probabilidad de cometer un error de tipo II es aceptable desde la perspectiva de la toma de decisiones. 

Análisis de potencia usando Python

El módulo stats.power del paquete statsmodels en Python contiene las funciones necesarias para realizar análisis de potencia para las pruebas estadísticas más utilizadas, como la prueba t, la prueba basada en normal, las pruebas F y la prueba de bondad de ajuste Chi-cuadrado. Su función solve_power toma 3 de las 4 variables mencionadas anteriormente como parámetros de entrada y calcula la cuarta variable restante.

Considere una prueba t de Student, que es una prueba de hipótesis estadística para comparar las medias de dos muestras de variables gaussianas. En un estudio piloto con los dos grupos de variables, N1 = 4, Mean1 = 90, SD1 = 5; N2 = 4, Mean2 = 85, SD2 = 5. La suposición, o hipótesis nula, de la prueba es que las poblaciones de muestra tienen la misma media. Dado que alfa generalmente se establece en 0,05 y la potencia en 0,80, el investigador debe preocuparse principalmente por el tamaño de la muestra y el tamaño del efecto. Determinemos el tamaño de muestra necesario para la prueba en la que es aceptable una potencia del 80 %, con un nivel de significación del 5 % y el tamaño del efecto esperado que se encontrará utilizando el estudio piloto. 

Ejemplo 1:

Primero, importe las bibliotecas relevantes. Calcule el tamaño del efecto utilizando la d de Cohen. La función TTestIndPower implementa cálculos de potencia estadística para la prueba t para dos muestras independientes. Del mismo modo, hay funciones para la prueba F, la prueba Z y la prueba Chi-cuadrado. A continuación, inicialice las variables para el análisis de potencia. Luego, usando la función solve_power, podemos obtener la variable faltante requerida, que es el tamaño de la muestra en este caso.

Código:

# import required modules
from math import sqrt
from statsmodels.stats.power import TTestIndPower
  
#calculation of effect size
# size of samples in pilot study
n1, n2 = 4, 4
  
# variance of samples in pilot study
s1, s2 = 5**2, 5**2
  
# calculate the pooled standard deviation 
# (Cohen's d)
s = sqrt(((n1 - 1) * s1 + (n2 - 1) * s2) / (n1 + n2 - 2))
  
# means of the samples
u1, u2 = 90, 85
  
# calculate the effect size
d = (u1 - u2) / s
print(f'Effect size: {d}')
  
# factors for power analysis
alpha = 0.05
power = 0.8
  
# perform power analysis to find sample size 
# for given effect
obj = TTestIndPower()
n = obj.solve_power(effect_size=d, alpha=alpha, power=power, 
                    ratio=1, alternative='two-sided')
  
print('Sample size/Number needed in each group: {:.3f}'.format(n))

Producción:

Effect size: 1.0
Sample size/Number needed in each group: 16.715

Por lo tanto, el número mínimo sugerido de muestras requeridas en cada grupo es 17 para tener un valor p significativo en la prueba t. Si procedemos y usamos una prueba t inferencial antes del análisis de potencia, podemos encontrar un valor de p no significativo aunque haya un gran efecto, probablemente debido al pequeño tamaño de la muestra (4).

Ejemplo 2:

Alternativamente, podemos probar el poder de un tamaño de muestra propuesto específico. 

Código:

from statsmodels.stats.power import TTestPower
  
  
power = TTestPower()
n_test = power.solve_power(nobs=40, effect_size = 0.5,
                           power = None, alpha = 0.05)
print('Power: {:.3f}'.format(n_test))

Producción:

Power: 0.869

Esto nos dice que un tamaño de muestra mínimo de 40 daría como resultado una potencia de 0,87. 

Ejemplo 3:

También podemos trazar curvas de potencia. Las curvas de potencia son gráficos de líneas que muestran cómo el cambio en el tamaño del efecto y el tamaño de la muestra afectan la potencia de la prueba estadística. La función plot_power() se puede utilizar para crear curvas de potencia. El argumento ‘dep_var’ especifica la variable dependiente (eje x) y puede ser ‘nobs’, ‘effect_size’ o ‘alpha’. Aquí, ‘nobs’ es el tamaño de la muestra y toma valores de array. Debido a esto, se crea una curva para cada valor del tamaño del efecto.

Supongamos un nivel de significación de 0,05 y exploremos el cambio en el tamaño de la muestra entre 5 y 100 con los tamaños de efecto estándar bajo, medio y alto de la d de Cohen.

Código:

# import required libraries
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.stats.power import TTestIndPower
  
  
# power analysis varying parameters
effect_sizes = np.array([0.2, 0.5, 0.8,1.3])
sample_sizes = np.array(range(5, 100))
  
# plot power curves
obj = TTestIndPower()
obj.plot_power(dep_var='nobs', nobs=sample_sizes,
               effect_size=effect_sizes)
  
plt.show()

Producción: