Propiedades de cierre de lenguajes regulares

Las propiedades de cierre en lenguajes regulares se definen como ciertas operaciones en lenguaje regular que están garantizadas para producir lenguaje regular. El cierre se refiere a alguna operación en un idioma, que da como resultado un nuevo idioma que es del mismo «tipo» que el que se operó originalmente, es decir, regular.

Los lenguajes regulares se cierran bajo las siguientes operaciones.

Considere que L y M son lenguajes regulares:

1. Kleen Closure:
   RS es una expresión regular cuyo idioma es L, M. R* es una expresión regular cuyo idioma es L*.
2. Cierre positivo:
   RS es una expresión regular cuyo idioma es L, M.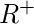 es una expresión regular cuyo idioma es .
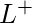3. Complemento:
   El complemento de una lengua L (respecto a un alfabeto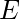 tal que 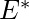contenga L) es 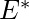–L. Como 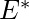seguramente es regular, el complemento de un lenguaje regular es siempre regular.
4. Operador Inverso:
   Dado el lenguaje L,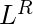 es el conjunto de strings cuya inversión está en L.
   Ejemplo: L = {0, 01, 100};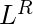
   = {0, 10, 001}.
   Prueba: Sea E una expresión regular para L. Mostramos cómo invertir E para proporcionar una expresión regular para .
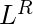5. Complemento:
   El complemento de una lengua L (respecto a un alfabeto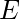 tal que 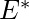contenga L) es 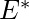–L. Como 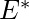seguramente es regular, el complemento de un lenguaje regular es siempre regular.
6. Unión:
   Sean L y M los idiomas de las expresiones regulares R y S, respectivamente. Entonces R+S es una expresión regular cuyo idioma es (LUM).
7. Intersección:
   Sean L y M los lenguajes de las expresiones regulares R y S, respectivamente, entonces es una expresión regular cuyo lenguaje es L intersección M.
   Prueba: Sean A y B DFA cuyos lenguajes son L y M, respectivamente. Construya C, el producto autómata de A y B hace que los estados finales de C sean los pares que consisten en los estados finales de A y B.
8. Operador de diferencia de conjuntos:
   si L y M son idiomas regulares, entonces también lo son L – M = strings en L pero no en M.

   Prueba: Sean A y B DFA cuyos lenguajes son L y M, respectivamente. Construya C, el producto autómata de A y B hace que los estados finales de C sean los pares, donde el estado A es final pero el estado B no lo es.

9. Homomorfismo:
   Un homomorfismo en un alfabeto es una función que da una string para cada símbolo en ese alfabeto. Ejemplo: h(0) = ab; h(1) =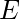 . Extender a strings por h(a1…an) =h(a1)…h(an). Ejemplo: h(01010) = ababab.

   Si L es un lenguaje regular y h es un homomorfismo en su alfabeto, entonces h(L)= {h(w) | w está en L} también es un lenguaje regular.
   Prueba: Sea E una expresión regular para L. Aplique h a cada símbolo en E. Lenguaje de la R resultante, E es h(L).

10. Homomorfismo inverso: Sea h un homomorfismo y L un idioma cuyo alfabeto es el idioma de salida de h. (L) = {w | h(w) está en L}.

Nota: Hay algunas propiedades más como el operador de diferencia simétrica, el operador de prefijo, la sustitución que se cierran bajo las propiedades de cierre del lenguaje normal.

Propiedades de decisión:
Aproximadamente todas las propiedades son decidibles en el caso de un autómata finito.

(i) Emptiness 
(ii) Non-emptiness 
(iii) Finiteness 
(iv) Infiniteness 
(v) Membership 
(vi) Equality  

Estos se explican a continuación a continuación.

(i) Vacío y no vacío:

• Paso 1: seleccione el estado que no se puede alcanzar desde los estados iniciales y elimínelos (elimine los estados inalcanzables).
• Paso 2: si la máquina resultante contiene al menos un estado final, entonces los autómatas finitos aceptan el lenguaje no vacío.
• Paso 3: si la máquina resultante está libre del estado final, entonces los autómatas finitos aceptan un lenguaje vacío.

(ii) Finitud e Infinitud:

• Paso 1: seleccione el estado que no se puede alcanzar desde el estado inicial y elimínelo (elimine los estados inalcanzables).
• Paso 2: seleccione el estado desde el que no podemos alcanzar el estado final y elimínelo (elimine los estados muertos).
• Paso 3: si la máquina resultante contiene bucles o ciclos, entonces los autómatas finitos aceptan un lenguaje infinito.
• Paso 4: si la máquina resultante no contiene bucles o ciclos, los autómatas finitos aceptan un lenguaje infinito.

(iii) Membresía:
La membresía es una propiedad para verificar que una string arbitraria sea aceptada o no por un autómata finito, es decir, sea miembro del lenguaje o no.

Sea M un autómata finito que acepta algunas strings sobre un alfabeto, y sea ‘w’ cualquier string definida sobre el alfabeto, si existe un camino de transición en M, que comienza en el estado inicial y termina en cualquiera del estado final, entonces la string ‘w’ es miembro de M, de lo contrario, ‘w’ no es miembro de M.

(iv) Igualdad:
se dice que dos autómatas de estado finito M1 y M2 son iguales si y solo si aceptan el mismo lenguaje. Minimice los autómatas de estado finito y el DFA mínimo será único.