Window Sliding Technique es una técnica computacional que tiene como objetivo reducir el uso de bucle anidado y reemplazarlo con un solo bucle, reduciendo así la complejidad del tiempo.
¿Qué es la ventana corrediza?
Considere una string larga conectada entre sí. Suponga que desea aplicar aceite en toda la string con las manos, sin verter el aceite desde arriba.
Una forma de hacerlo es:
- recoger un poco de aceite,
- aplicar en una sección de la string,
- luego vuelve a recoger un poco de aceite
- luego aplíquelo a la siguiente sección donde aún no se ha aplicado aceite
- y así sucesivamente hasta engrasar toda la string.
Otra forma de hacerlo es usar un paño, sumergirlo en aceite y luego sujetar un extremo de la string con este paño. Luego, en lugar de volver a mojarlo una y otra vez, simplemente desliza el paño con la mano en la siguiente sección, y luego, y así sucesivamente hasta el otro extremo.
La segunda forma se conoce como la técnica de la ventana deslizante y la parte que se desliza de un extremo a otro se conoce como ventana deslizante .

técnica de la ventana corredera
Requisito previo para usar la técnica de la ventana deslizante
El uso de la técnica de Ventana Deslizante se puede hacer en un escenario muy específico, donde el tamaño de la ventana para el cálculo es fijo a lo largo del bucle anidado completo. Solo entonces se puede reducir la complejidad del tiempo.
¿Cómo utilizar la Técnica de la Ventana Deslizante?
El uso general de la técnica de la ventana deslizante se puede demostrar de la siguiente manera:
- Encuentre el tamaño de ventana requerido
- Calcule el resultado para la primera ventana, es decir, desde el inicio de la estructura de datos
- Luego use un bucle para deslizar la ventana en 1 y siga calculando el resultado ventana por ventana.
Ejemplos para ilustrar el uso de la técnica de la ventana deslizante
Ejemplo: Dada una array de enteros de tamaño ‘n’, nuestro objetivo es calcular la suma máxima de ‘k’ elementos consecutivos en la array.
Entrada: arr[] = {100, 200, 300, 400}, k = 2
Salida: 700Entrada: arr[] = {1, 4, 2, 10, 23, 3, 1, 0, 20}, k = 4
Salida: 39
Obtenemos la suma máxima sumando el subarreglo {4, 2, 10, 23} de tamaño 4.Entrada: arr[] = {2, 3}, k = 3
Salida: no válido
No hay subarreglo de tamaño 3 ya que el tamaño de todo el arreglo es 2.
Enfoque ingenuo: Entonces, analicemos el problema con el enfoque de fuerza bruta . Comenzamos con el primer índice y sumamos hasta el k-ésimo elemento. Lo hacemos para todos los posibles bloques consecutivos o grupos de k elementos. Este método requiere un bucle for anidado, el bucle for externo comienza con el elemento inicial del bloque de k elementos y el bucle interno o anidado se sumará hasta el k-ésimo elemento.
Considere la siguiente implementación:
C++
// O(n*k) solution for finding maximum sum of
// a subarray of size k
#include <bits/stdc++.h>
using namespace std;
// Returns maximum sum in a subarray of size k.
int maxSum(int arr[], int n, int k)
{
// Initialize result
int max_sum = INT_MIN;
// Consider all blocks starting with i.
for (int i = 0; i < n - k + 1; i++) {
int current_sum = 0;
for (int j = 0; j < k; j++)
current_sum = current_sum + arr[i + j];
// Update result if required.
max_sum = max(current_sum, max_sum);
}
return max_sum;
}
// Driver code
int main()
{
int arr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
int k = 4;
int n = sizeof(arr) / sizeof(arr[0]);
cout << maxSum(arr, n, k);
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
C
// O(n*k) solution for finding maximum sum of
// a subarray of size k
#include <limits.h>
#include <math.h>
#include <stdio.h>
// Find maximum between two numbers.
int max(int num1, int num2)
{
return (num1 > num2) ? num1 : num2;
}
// Returns maximum sum in a subarray of size k.
int maxSum(int arr[], int n, int k)
{
// Initialize result
int max_sum = INT_MIN;
// Consider all blocks starting with i.
for (int i = 0; i < n - k + 1; i++) {
int current_sum = 0;
for (int j = 0; j < k; j++)
current_sum = current_sum + arr[i + j];
// Update result if required.
max_sum = max(current_sum, max_sum);
}
return max_sum;
}
// Driver code
int main()
{
int arr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
int k = 4;
int n = sizeof(arr) / sizeof(arr[0]);
printf("%d", maxSum(arr, n, k));
return 0;
}
// This code is contributed by Aditya Kumar (adityakumar129)
Java
// Java code O(n*k) solution for finding maximum sum of
// a subarray of size k
class GFG {
// Returns maximum sum in
// a subarray of size k.
static int maxSum(int arr[], int n, int k)
{
// Initialize result
int max_sum = Integer.MIN_VALUE;
// Consider all blocks starting with i.
for (int i = 0; i < n - k + 1; i++) {
int current_sum = 0;
for (int j = 0; j < k; j++)
current_sum = current_sum + arr[i + j];
// Update result if required.
max_sum = Math.max(current_sum, max_sum);
}
return max_sum;
}
// Driver code
public static void main(String[] args)
{
int arr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
int k = 4;
int n = arr.length;
System.out.println(maxSum(arr, n, k));
}
}
// This code is contributed by Aditya Kumar (adityakumar129)
Python3
# code import sys # O(n * k) solution for finding # maximum sum of a subarray of size k INT_MIN = -sys.maxsize - 1 # Returns maximum sum in a # subarray of size k. def maxSum(arr, n, k): # Initialize result max_sum = INT_MIN # Consider all blocks # starting with i. for i in range(n - k + 1): current_sum = 0 for j in range(k): current_sum = current_sum + arr[i + j] # Update result if required. max_sum = max(current_sum, max_sum) return max_sum # Driver code arr = [1, 4, 2, 10, 2, 3, 1, 0, 20] k = 4 n = len(arr) print(maxSum(arr, n, k)) # This code is contributed by mits
C#
// C# code here O(n*k) solution for
// finding maximum sum of a subarray
// of size k
using System;
class GFG {
// Returns maximum sum in a
// subarray of size k.
static int maxSum(int[] arr, int n, int k)
{
// Initialize result
int max_sum = int.MinValue;
// Consider all blocks starting
// with i.
for (int i = 0; i < n - k + 1; i++) {
int current_sum = 0;
for (int j = 0; j < k; j++)
current_sum = current_sum + arr[i + j];
// Update result if required.
max_sum = Math.Max(current_sum, max_sum);
}
return max_sum;
}
// Driver code
public static void Main()
{
int[] arr = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
int k = 4;
int n = arr.Length;
Console.WriteLine(maxSum(arr, n, k));
}
}
// This code is contributed by anuj_67.
PHP
<?php
// code
?>
<?php
// O(n*k) solution for finding maximum sum of
// a subarray of size k
// Returns maximum sum in a subarray of size k.
function maxSum($arr, $n, $k)
{
// Initialize result
$max_sum = PHP_INT_MIN ;
// Consider all blocks
// starting with i.
for ( $i = 0; $i < $n - $k + 1; $i++)
{
$current_sum = 0;
for ( $j = 0; $j < $k; $j++)
$current_sum = $current_sum +
$arr[$i + $j];
// Update result if required.
$max_sum = max($current_sum, $max_sum );
}
return $max_sum;
}
// Driver code
$arr = array(1, 4, 2, 10, 2, 3, 1, 0, 20);
$k = 4;
$n = count($arr);
echo maxSum($arr, $n, $k);
// This code is contributed by anuj_67.
?>
Javascript
<script>
// O(n*k) solution for finding maximum sum of
// a subarray of size k
// Returns maximum sum in a subarray of size k.
function maxSum( arr, n, k){
// Initialize result
let max_sum = Number.MIN_VALUE;
// Consider all blocks starting with i.
for (let i = 0; i < n - k + 1; i++) {
let current_sum = 0;
for (let j = 0; j < k; j++)
current_sum = current_sum + arr[i + j];
// Update result if required.
max_sum = Math.max(current_sum, max_sum);
}
return max_sum;
}
// Driver code
let arr = [ 1, 4, 2, 10, 2, 3, 1, 0, 20 ];
let k = 4;
let n = arr.length;
document.write(maxSum(arr, n, k));
</script>
24
Se puede observar en el código anterior que la complejidad del tiempo es O(k*n) ya que contiene dos bucles anidados.
Técnica de la ventana deslizante: la técnica se puede entender mejor con el panel de la ventana en bus, considere una ventana de longitud n y el panel que está fijo en ella de longitud k . Considere, inicialmente el panel está en el extremo izquierdo, es decir, a 0 unidades desde la izquierda. Ahora, correlacione la ventana con la array arr[] de tamaño n y el panel con los elementos current_sum de tamaño k. Ahora, si aplicamos una fuerza en la ventana de tal manera que se mueva una unidad de distancia hacia adelante. El panel cubrirá los siguientes k elementos consecutivos.
Aplicación de la técnica de la ventana corredera :
- Calculamos la suma de los primeros k elementos de n términos usando un bucle lineal y almacenamos la suma en la variable window_sum.
- Luego, pasaremos linealmente sobre la array hasta que llegue al final y, al mismo tiempo, realizaremos un seguimiento de la suma máxima.
- Para obtener la suma actual del bloque de k elementos, simplemente reste el primer elemento del bloque anterior y agregue el último elemento del bloque actual.
La siguiente representación aclarará cómo se desliza la ventana sobre la array.
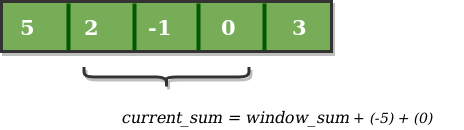
Considere una array arr[] = {5, 2, -1, 0, 3} y el valor de k = 3 y n = 5
Esta es la fase inicial en la que hemos calculado la suma de la ventana inicial a partir del índice 0. En esta etapa, la suma de la ventana es 6. Ahora, establecemos la suma_máxima como ventana_actual, es decir, 6.
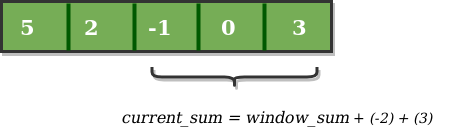
Ahora, deslizamos nuestra ventana por un índice de unidad. Por lo tanto, ahora descarta 5 de la ventana y agrega 0 a la ventana. Por lo tanto, obtendremos la suma de nuestra nueva ventana restando 5 y luego sumando 0. Entonces, nuestra suma de ventana ahora se convierte en 1. Ahora, compararemos esta suma de ventana con la suma_máxima. Como es más pequeño, no cambiaremos la suma_máxima.
De manera similar, ahora una vez más deslizamos nuestra ventana por un índice unitario y obtenemos que la nueva suma de la ventana sea 2. Nuevamente verificamos si la suma de esta ventana actual es mayor que la suma_máxima hasta ahora. Una vez más, es más pequeño, por lo que no cambiamos la suma_máxima.
Por lo tanto, para la array anterior, nuestra suma_máxima es 6.
A continuación se muestra el código para el enfoque anterior:
C++
// O(n) solution for finding maximum sum of
// a subarray of size k
#include <iostream>
using namespace std;
// Returns maximum sum in a subarray of size k.
int maxSum(int arr[], int n, int k)
{
// n must be greater
if (n < k) {
cout << "Invalid";
return -1;
}
// Compute sum of first window of size k
int max_sum = 0;
for (int i = 0; i < k; i++)
max_sum += arr[i];
// Compute sums of remaining windows by
// removing first element of previous
// window and adding last element of
// current window.
int window_sum = max_sum;
for (int i = k; i < n; i++) {
window_sum += arr[i] - arr[i - k];
max_sum = max(max_sum, window_sum);
}
return max_sum;
}
// Driver code
int main()
{
int arr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
int k = 4;
int n = sizeof(arr) / sizeof(arr[0]);
cout << maxSum(arr, n, k);
return 0;
}
Java
// Java code for
// O(n) solution for finding
// maximum sum of a subarray
// of size k
class GFG {
// Returns maximum sum in
// a subarray of size k.
static int maxSum(int arr[], int n, int k)
{
// n must be greater
if (n < k) {
System.out.println("Invalid");
return -1;
}
// Compute sum of first window of size k
int max_sum = 0;
for (int i = 0; i < k; i++)
max_sum += arr[i];
// Compute sums of remaining windows by
// removing first element of previous
// window and adding last element of
// current window.
int window_sum = max_sum;
for (int i = k; i < n; i++) {
window_sum += arr[i] - arr[i - k];
max_sum = Math.max(max_sum, window_sum);
}
return max_sum;
}
// Driver code
public static void main(String[] args)
{
int arr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
int k = 4;
int n = arr.length;
System.out.println(maxSum(arr, n, k));
}
}
// This code is contributed
// by prerna saini.
Python3
# O(n) solution for finding
# maximum sum of a subarray of size k
def maxSum(arr, k):
# length of the array
n = len(arr)
# n must be greater than k
if n < k:
print("Invalid")
return -1
# Compute sum of first window of size k
window_sum = sum(arr[:k])
# first sum available
max_sum = window_sum
# Compute the sums of remaining windows by
# removing first element of previous
# window and adding last element of
# the current window.
for i in range(n - k):
window_sum = window_sum - arr[i] + arr[i + k]
max_sum = max(window_sum, max_sum)
return max_sum
# Driver code
arr = [1, 4, 2, 10, 2, 3, 1, 0, 20]
k = 4
print(maxSum(arr, k))
# This code is contributed by Kyle McClay
C#
// C# code for O(n) solution for finding
// maximum sum of a subarray of size k
using System;
class GFG {
// Returns maximum sum in
// a subarray of size k.
static int maxSum(int[] arr, int n, int k)
{
// n must be greater
if (n < k) {
Console.WriteLine("Invalid");
return -1;
}
// Compute sum of first window of size k
int max_sum = 0;
for (int i = 0; i < k; i++)
max_sum += arr[i];
// Compute sums of remaining windows by
// removing first element of previous
// window and adding last element of
// current window.
int window_sum = max_sum;
for (int i = k; i < n; i++) {
window_sum += arr[i] - arr[i - k];
max_sum = Math.Max(max_sum, window_sum);
}
return max_sum;
}
// Driver code
public static void Main()
{
int[] arr = { 1, 4, 2, 10, 2, 3, 1, 0, 20 };
int k = 4;
int n = arr.Length;
Console.WriteLine(maxSum(arr, n, k));
}
}
// This code is contributed by anuj_67.
PHP
<?php
// O(n) solution for finding maximum sum of
// a subarray of size k
// Returns maximum sum in a
// subarray of size k.
function maxSum( $arr, $n, $k)
{
// n must be greater
if ($n < $k)
{
echo "Invalid";
return -1;
}
// Compute sum of first
// window of size k
$max_sum = 0;
for($i = 0; $i < $k; $i++)
$max_sum += $arr[$i];
// Compute sums of remaining windows by
// removing first element of previous
// window and adding last element of
// current window.
$window_sum = $max_sum;
for ($i = $k; $i < $n; $i++)
{
$window_sum += $arr[$i] - $arr[$i - $k];
$max_sum = max($max_sum, $window_sum);
}
return $max_sum;
}
// Driver code
$arr = array(1, 4, 2, 10, 2, 3, 1, 0, 20);
$k = 4;
$n = count($arr);
echo maxSum($arr, $n, $k);
// This code is contributed by anuj_67
?>
Javascript
<script>
// Javascript code for
// O(n) solution for finding
// maximum sum of a subarray
// of size k
function maxSum(arr, n, k) {
let max = 0;
let sum = 0;
// find initial sum of first k elements
for (let i = 0; i < k; i++) {
sum += arr[i];
max = sum;
}
// iterate the array once
// and increment the right edge
for (let i = k; i < n; i++) {
sum += arr[i] - arr[i - k];
// compare if sum is more than max,
// if yes then replace
// max with new sum value
if (sum > max) {
max = sum;
}
}
return max;
}
// Driver code
let arr = [1, 4, 2, 10, 2, 3, 1, 0, 20];
let k = 4;
let n = arr.length;
document.write(maxSum(arr, n, k));
</script>
24
Ahora, es bastante obvio que la complejidad del tiempo es lineal, ya que podemos ver que solo se ejecuta un bucle en nuestro código. Por lo tanto, nuestra Complejidad de Tiempo es O(n) .
Podemos usar esta técnica para encontrar max/min k-subarreglo, XOR, producto, suma, etc. Consulte los problemas de ventana deslizante para tales problemas.
- Artículos recientes sobre la técnica de deslizamiento de ventanas
- Preguntas de práctica sobre deslizamiento de ventanas
- DSA a su propio ritmo: el curso más utilizado y confiable sobre DSA
Este artículo es una contribución de Kanika Thakral . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA