Redes neuronales convolucionales separables en profundidad

La convolución es una operación matemática muy importante en las redes neuronales artificiales (ANN) . Las redes neuronales convolucionales (CNN) se pueden usar para aprender funciones y clasificar datos con la ayuda de marcos de imagen. Hay muchos tipos de CNN. Una clase de CNN son las redes neuronales convolucionales separables en profundidad .

Este tipo de CNN se usa ampliamente debido a las siguientes dos razones:

• Tienen una menor cantidad de parámetros para ajustar en comparación con las CNN estándar, lo que reduce el sobreajuste .
• Son computacionalmente más baratos debido a la menor cantidad de cómputos, lo que los hace adecuados para aplicaciones de visión móvil.

Algunas aplicaciones importantes de este tipo de CNN son MobileNet , Xception (ambas propuestas por Google)

Este artículo explica la arquitectura y las operaciones utilizadas por las redes convolucionales separables en profundidad y deriva su eficiencia sobre las redes neuronales de convolución simples.

Comprensión de la operación de convolución normal

Supongamos que hay datos de entrada de tamaño Df x Df x M , donde Df x Df puede ser el tamaño de la imagen y M es el número de canales (3 para una imagen RGB). Supongamos que hay N filtros/núcleos de tamaño Dk x Dk x M. Si se realiza una operación de convolución normal, entonces, el tamaño de salida será Dp x Dp x N.

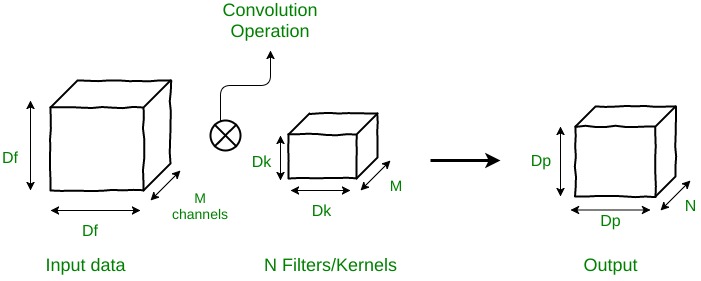
El número de multiplicaciones en 1 operación de convolución = tamaño del filtro = Dk x Dk x M

Como hay N filtros y cada filtro se desliza vertical y horizontalmente Dp veces,

el número total de multiplicaciones se convierte en N x Dp x Dp x (Multiplicaciones por convolución)

Entonces, para la operación de convolución normal

Número total de multiplicaciones = N x Dp ² x Dk ² x M

Circunvoluciones separables en profundidad

Ahora mire las circunvoluciones separables en profundidad. Este proceso se divide en 2 operaciones:

1. Circunvoluciones en profundidad
2. Convoluciones puntuales

1. CONVOLUCIÓN SABIA DE PROFUNDIDAD

   En la operación profunda , la convolución se aplica a un solo canal a la vez, a diferencia de las CNN estándar en las que se realiza para todos los canales M. Así que aquí los filtros/núcleos serán de tamaño Dk x Dk x 1 . Dado que hay M canales en los datos de entrada, se requieren M filtros de este tipo. La salida será de tamaño Dp x Dp x M.

   

   Costo de esta operación:

   Una sola operación de convolución requiere multiplicaciones Dk x Dk.

   Dado que el filtro se desliza por tiempos Dp x Dp en todos los canales M,

   el número total de multiplicaciones es igual a M x Dp x Dp x Dk x Dk

   Entonces, para la operación de convolución en profundidad

   Número total de multiplicaciones = M x Dk ² x Dp ²

2. PUNTO SABIO CONVOLUCIÓN

   En la operación puntual , se aplica una operación de convolución 1×1 en los canales M. Entonces, el tamaño del filtro para esta operación será 1 x 1 x M. Digamos que usamos N filtros de este tipo, el tamaño de salida se convierte en Dp x Dp x N.

   

   Costo de esta operación:

   Una sola operación de convolución requiere 1 x M multiplicaciones.

   Dado que el filtro se desliza por Dp x Dp veces,

   el número total de multiplicaciones es igual a M x Dp x Dp x (nº de filtros)

   Entonces, para la operación de convolución puntual

   Número total de multiplicaciones = M x Dp ² x N

   Por lo tanto, para el funcionamiento general:

   
   Multiplicaciones totales = Conversión sabia de profundidad. multiplicaciones + Punto sabio conv. multiplicaciones

   Total de multiplicaciones = M * Dk ² * Dp ² + M * Dp ² * N = M * Dp ² * (Dk ² + n)

   Entonces, para la operación de convolución separable en profundidad

   Número total de multiplicaciones = M x Dp ² x (Dk ² + N)

   Comparación entre las complejidades de estos tipos de operaciones de convolución

   <

   Tipo de convolución	Complejidad
   Estándar	N x profundidad 2 x profundidad 2 x M
   Separable en profundidad	M x Dp 2 x (Dk 2 + N)

     Complexity of depth wise separable convolutions 
   --------------------------------------------------   =  RATIO ( R )
          Complexity of standard convolution 
   

   Al resolver:

   Relación (R) = 1/N + 1/Dk ²

   Como ejemplo, considere N = 100 y Dk = 512. Entonces la relación R = 0.010004

   Esto significa que la red de convolución separable en profundidad, en este ejemplo, realiza multiplicaciones 100 veces menores en comparación con una red neuronal constitucional estándar.

   Esto implica que podemos implementar modelos de redes neuronales de convolución más rápidos sin perder mucha precisión.