Requisito previo: introducción de FA , expresiones regulares, gramática y lenguaje , diseño de FA a partir de expresiones regulares
Hay dos métodos para convertir FA en expresión regular:
1. Método de eliminación de estado:
- Paso 1:
si el estado de inicio es un estado de aceptación o tiene transiciones, agregue un nuevo estado de inicio de no aceptación y agregue una transición € entre el nuevo estado de inicio y el estado de inicio anterior. - Paso 2:
si hay más de un estado de aceptación o si el único estado de aceptación tiene transiciones, agregue un nuevo estado de aceptación, haga que todos los demás estados no acepten y agregue una transición € de cada estado de aceptación anterior al nuevo estado de aceptación estado. - Paso 3:
para cada estado de no aceptación de no inicio, elimine el estado y actualice las transiciones en consecuencia.
Ejemplo :-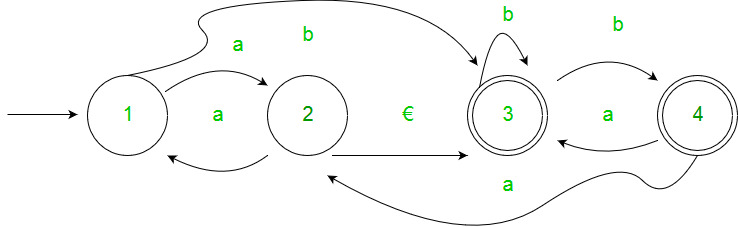
Solución : –
Paso 1
Paso 2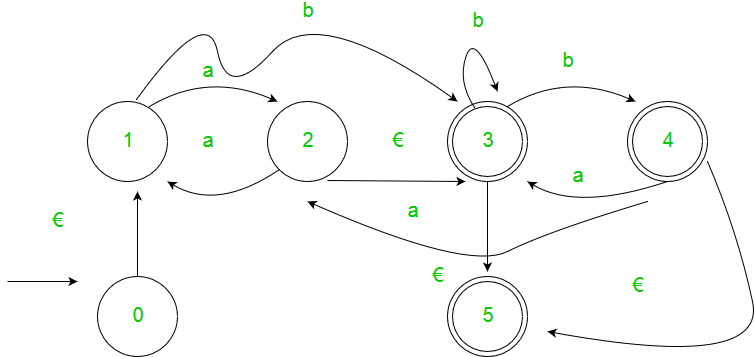
Paso 3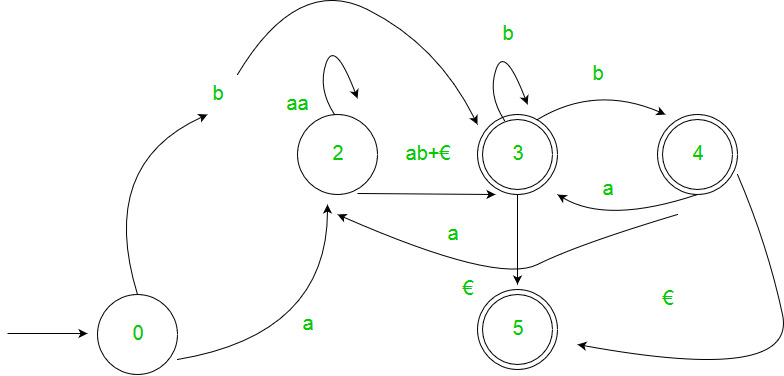
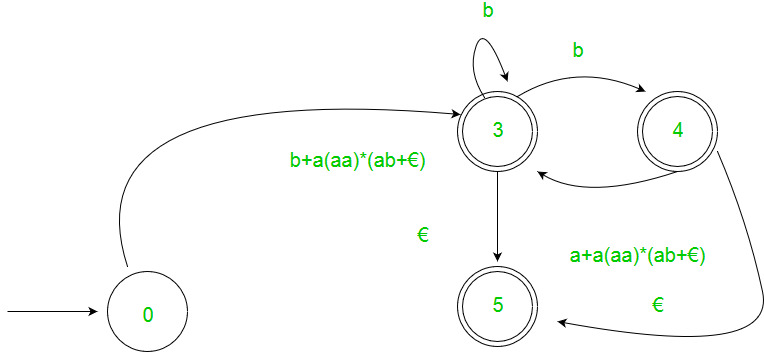
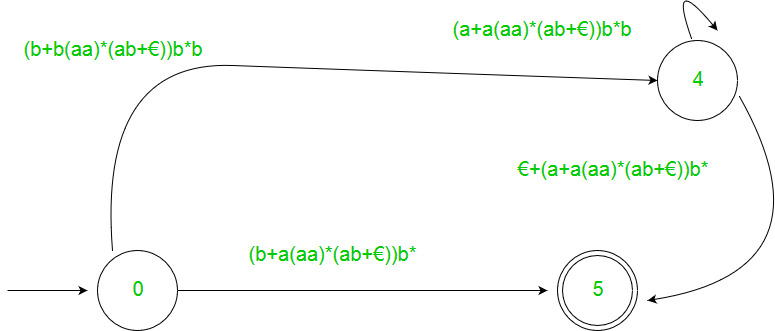

2. Teorema de Arden – Sean P y Q 2 expresiones regulares. Si P no contiene una string nula, entonces la siguiente ecuación en R, a saber, R = Q + RP, tiene una solución única por R = QP*
Suposiciones –
- El diagrama de transición no debe tener movimientos €.
- Debe tener un solo estado inicial.
Uso del teorema de Arden para encontrar la expresión regular de autómatas finitos deterministas:
- Para obtener la expresión regular de los autómatas, primero creamos ecuaciones de la forma dada para todos los estados
q 1 = q 1 w 11 +q 2 w 21 +…+q n w n1 +€ (q 1 es el estado inicial)
q 2 = q 1 w 12 +q 2 w 22 +…+q norte w n2 . . . q norte = q 1 w 1n +q 2 w 2n +…+q norte wnn
w ij es la expresión regular que representa el conjunto de etiquetas de aristas de q i a q jNota: para bordes paralelos, habrá tantas expresiones para ese estado en la expresión.
- Luego resolvemos estas ecuaciones para obtener la ecuación para q i en términos de w ij y esa expresión es la solución requerida, donde q i es un estado final.
Ejemplo :-
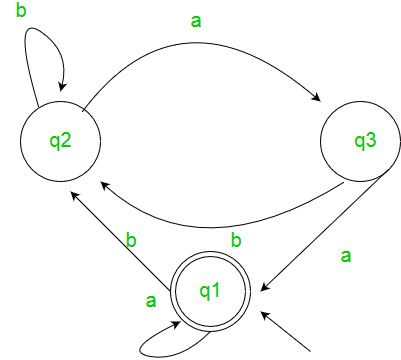
Solución : –
Aquí el estado inicial es q 2 y el estado final es q 1 .
Las ecuaciones para los tres estados q 1 , q 2 y q 3 son las siguientes ?
q 1 = q 1 a + q 3 a + € ( € el movimiento es porque q 1 es el estado inicial)
q 2 = q 1 b + q 2 b + q 3 b
q 3 = q 2 a
Ahora resolveremos estos tres ecuaciones?
q 2 = q 1 segundo + q 2b + q 3 b
= q 1 b + q 2 b + (q 2 a)b (Sustituyendo el valor de q 3 )
= q 1 b + q 2 (b + ab)
= q 1 b (b + ab)* ( Aplicando el teorema de Arden)
q 1 = q 1 a + q 3 a + €
= q 1 a + q 2 aa + € (Sustituyendo el valor de q 3 )
= q 1 a + q 1 b(b + ab*)aa + € (Sustituyendo el valor de q 2 )
= q 1 (a + b(b + ab)*aa) + €
= € (a+ b(b + ab)*aa)*
= (a + b(b + ab)*aa)*
Por tanto, la expresión regular es (a + b(b + ab)*aa)*.
Preguntas de GATE CS Corner
Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.