Extraiga planos de bits de una imagen en Matlab

La imagen es básicamente una combinación de información de píxeles individuales (puntos). Cuando escribimos que la imagen tiene un tamaño de 620 X 480, significa que la imagen tiene 620 píxeles en dirección horizontal y 480 píxeles en dirección vertical. Entonces, en total hay 620 X 480 píxeles y cada píxel contiene información sobre la imagen.

Las imágenes en escala de grises son básicamente aquellas imágenes de las que decimos imágenes en blanco y negro. Cada píxel de la imagen en escala de grises tiene un valor entre 0 y 255 que decide en qué posición la imagen será negra y en qué posición será blanca.

Si el valor del píxel es 0 , significa que el color del píxel será completamente negro y si el valor del píxel es 255 , ese píxel será completamente blanco y el píxel que tenga un valor intermedio tendrá tonos de blanco y negro.

Nos dan una imagen en escala de grises . Dado que el valor de píxel de la imagen en escala de grises se encuentra entre 0 y 255 , su información se contiene utilizando 8 bits . Entonces, podemos dividir esa imagen en 8 planos (8 imágenes binarias ). Las imágenes binarias son aquellas imágenes cuyo valor de píxel puede ser 0 o 1 .

Entonces, nuestra tarea es extraer cada plano de bits de la imagen original para hacer 8 imágenes binarias

Deje que un píxel particular de la imagen en escala de grises tenga un valor de 212. Por lo tanto, su valor binario será 11010100. Por lo tanto, su primer bit es 0, el segundo es 0, el tercero es 1, el cuarto es 0, el quinto es 1, el sexto es 0, el séptimo es 1 , 8th es 1. De esta manera, tomaremos estos 8 bits de todos los píxeles y dibujaremos 8 imágenes binarias. Tenemos que hacer esto con todos los píxeles y generar nuevas imágenes.

A continuación se muestra la implementación de la idea anterior en matlab.

% clearing the output screen
clc;
  
% reading image's pixel in c
c = imread('cameraman.tif');
  
% storing image information in cd
cd = double(c);
  
% extracting all bit one by one
% from 1st to 8th in variable
% from c1 to c8 respectively
c1 = mod(cd, 2);
c2 = mod(floor(cd/2), 2);
c3 = mod(floor(cd/4), 2);
c4 = mod(floor(cd/8), 2);
c5 = mod(floor(cd/16), 2);
c6 = mod(floor(cd/32), 2);
c7 = mod(floor(cd/64), 2);
c8 = mod(floor(cd/128), 2);
  
% combining image again to form equivalent to original grayscale image
cc = (2 * (2 * (2 * (2 * (2 * (2 * (2 * c8 + c7) + c6) + c5) + c4) + c3) + c2) + c1);
  
% plotting original image in first subplot
subplot(2, 5, 1);
imshow(c);
title('Original Image');
  
% plotting binary image having extracted bit from 1st to 8th
% in subplot from 2nd to 9th
subplot(2, 5, 2);
imshow(c1);
title('Bit Plane 1');
subplot(2, 5, 3);
imshow(c2);
title('Bit Plane 2');
subplot(2, 5, 4);
imshow(c3);
title('Bit Plane 3');
subplot(2, 5, 5);
imshow(c4);
title('Bit Plane 4');
subplot(2, 5, 6);
imshow(c5);
title('Bit Plane 5');
subplot(2, 5, 7);
imshow(c6);
title('Bit Plane 6');
subplot(2, 5, 8);
imshow(c7);
title('Bit Plane 7');
subplot(2, 5, 9);
imshow(c8);
title('Bit Plane 8');
  
% plotting recombined image in 10th subplot
subplot(2, 5, 10);
imshow(uint8(cc));
title('Recombined Image');

A continuación se muestra una captura de pantalla del resultado obtenido, que son 10 imágenes en 10 subparcelas. El primero es la imagen original. La segunda imagen es una representación de la imagen extraída del primer bit (bit menos significativo), la tercera es del segundo bit y así sucesivamente. La novena imagen se extrae como imagen de octavo bit (bit más significativo) y la décima imagen se obtiene después de recombinar los 8 bits extraídos.

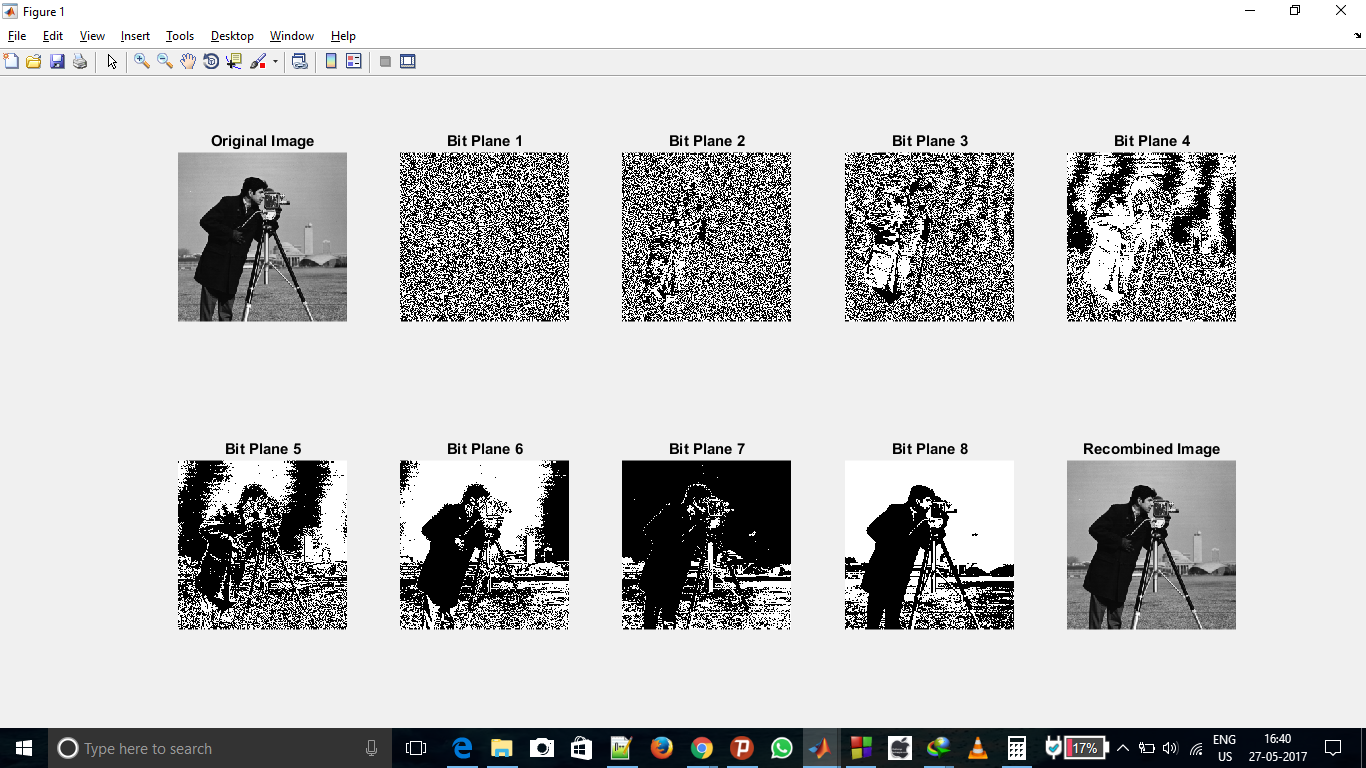
Referencia de la imagen original: Aquí

Este artículo es una contribución de Aditya Kumar . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.