Resolvamos el clásico acertijo de «moneda falsa» usando árboles de decisión. Existen las dos variantes diferentes del rompecabezas que se detallan a continuación. Proporciono una descripción de los dos acertijos a continuación, intente resolverlos por su cuenta, suponga que N = 8.
Fácil: dada una balanza justa de dos platillos y N monedas idénticas, de las cuales solo una moneda es más liviana (o más pesada) . Para sacar la moneda impar, ¿cuántos números mínimos de pesaje se requieren en el peor de los casos?
Difícil: dada una balanza justa de dos platillos y N monedas de aspecto idéntico, de las cuales solo una moneda puede estar defectuosa. ¿Cómo podemos rastrear qué moneda, si es que hay alguna, es impar y también determinar si es más liviana o más pesada en un número mínimo de intentos en el peor de los casos?
Comencemos con ejemplos relativamente simples. Después de leer cada problema, trate de resolverlo por su cuenta.
Problema 1: (Fácil)
Dadas 5 monedas de las cuales una moneda es más ligera . En el peor de los casos, ¿cuántos números mínimos de pesaje se requieren para calcular la moneda impar?
Nombra las monedas como 1, 2, 3, 4 y 5. Sabemos que una moneda es más liviana. Teniendo en cuenta el mejor resultado del balance, podemos agrupar las monedas de dos formas diferentes, [(1, 2), (3, 4) y (5)], o [(12), (34) y (5)]. Podemos descartar fácilmente grupos como [(123) y (45)], ya que obtendremos una respuesta obvia. Cualquier otra combinación caerá en uno de estos dos grupos, como [(2)(45) y (13)], etc.
Considere el primer grupo, pares (1, 2) y (3, 4). Podemos comprobar (1, 2), si son iguales seguimos con (3, 4). Necesitamos dos pesajes en el peor de los casos. La misma analogía se puede aplicar cuando la moneda es más pesada.
Con el segundo grupo, pesa (12) y (34). Si la balanza (5) está defectuosa, de lo contrario, elige el par más ligero, y necesitamos un pesaje más para encontrar el impar.
Ambas combinaciones necesitan dos pesajes en caso de 5 monedas con información previa de que una moneda es más ligera.
Análisis: En general, si sabemos que la moneda es pesada o liviana, podemos rastrear la moneda en log 3 (N) intentos (redondeado al siguiente entero). Si representamos el resultado del equilibrio como un árbol ternario, cada hoja representa un resultado. Dado que cualquier moneda entre N monedas puede ser defectuosa, necesitamos obtener un árbol de 3 arios que tenga un mínimo de N hojas. Un árbol 3-ario en el k-ésimo nivel tendrá 3 k hojas y por lo tanto necesitamos 3 k >= N.
Es decir, en k ensayos podemos examinar hasta 3 k monedas, si sabemos si la moneda defectuosa es más pesada o más ligera. Dado que una moneda es más pesada, comprueba que 3 intentos son suficientes para encontrar la moneda impar entre 12 monedas, porque 3 2 < 12 < 3 3 .
Problema 2: (Difícil)
Nos dan 4 monedas, de las cuales solo una puede estar defectuosa. No sabemos si todas las monedas son genuinas o si hay alguna defectuosa. ¿Cuántos números de pesaje se requieren en el peor de los casos para calcular la moneda impar, si está presente? También tenemos que decir si es más pesado o más ligero.
Del análisis anterior podemos pensar que k = 2 intentos son suficientes, ya que un árbol ario de dos niveles produce 9 hojas, lo que es mayor que N = 4 (lea el problema una vez más). Tenga en cuenta que es imposible resolver el problema de más de 4 monedas en dos pesajes. El árbol de decisión confirma el hecho (tratar de dibujar).
Podemos agrupar las monedas de dos formas diferentes, [(12, 34)] o [(1, 2) y (3, 4)]. Consideremos la combinación (12, 34), el árbol de decisión correspondiente se muestra a continuación. Las hojas azules son resultados válidos y las hojas rojas son casos imposibles. Llegamos a casos imposibles debido a las suposiciones hechas anteriormente en el camino.

El resultado puede ser (12) < (34), es decir, vamos al subárbol izquierdo o (12) > (34), es decir, vamos al subárbol derecho.
El subárbol izquierdo es posible de dos maneras,
- A) 1 o 2 pueden ser más claros O
- B) 3 o 4 pueden ser más pesados.
Más adelante en el subárbol izquierdo, como segundo ensayo, pesamos (1, 2) o (3, 4). Consideremos (3, 4) como la analogía para (1, 2) es similar. El resultado del segundo camino puede ser de tres maneras.
- A) (3) < (4) dando 4 como moneda defectuosa más pesada, O
- B) (3) > (4) dando 3 como moneda defectuosa más pesada O
- C) (3) = (4), generando ambigüedad. Aquí necesitamos un pesaje más para comparar una moneda genuina con 1 o 2. En la figura tomé (3, 2) donde 3 se confirma como genuina. Podemos obtener (3) > (2) en el que 2 es más claro, o (3) = (2) en el que 1 es más claro. Tenga en cuenta que es imposible obtener (3) < (2), contradice nuestra suposición inclinada hacia el lado izquierdo.
Del mismo modo podemos analizar el subárbol derecho. También necesitamos dos pesajes más en el subárbol derecho.
En general, necesitamos 3 pesajes para rastrear la moneda impar. Tenga en cuenta que no podemos utilizar dos resultados de árboles triarios. Además, el árbol no es un árbol completo, la rama central terminó después del primer pesaje. De hecho, podemos obtener 27 hojas de un árbol 3-ario completo de 3 niveles, pero solo obtuvimos 11 hojas, incluidos los casos imposibles.
Análisis: dadas N monedas, todas pueden ser genuinas o solo una moneda es defectuosa. Necesitamos un árbol de decisión con al menos (2N + 1) hojas que correspondan a las salidas. Porque puede haber N hojas para ser más ligeras, o N hojas para ser más pesadas o un caso genuino, en total (2N + 1) hojas.
Como se explicó anteriormente, el árbol ternario en el nivel k puede tener un máximo de 3 k hojas y necesitamos un árbol con hojas de 3 k > (2N + 1).
En otras palabras, necesitamos al menos k > log 3 (2N + 1) pesando para encontrar el defectuoso.
Observe la figura anterior que no todas las ramas están generando hojas, es decir, nos faltan salidas válidas en algunas ramas que conducen a una mayor cantidad de ensayos. Cuando sea posible, debemos agrupar las monedas de tal manera que cada rama produzca una salida válida (en términos simples, genere un árbol completo de 3 arios). El problema 4 describe este enfoque de 12 monedas.
Problema 3: (Caso especial de balanza de dos platillos)
Nos dan 5 monedas, un grupo de 4 monedas de las cuales una moneda es defectuosa ( no sabemos si es más pesada o más liviana) y una moneda es genuina. ¿Cuántos pesajes se requieren en el peor de los casos para determinar si la moneda impar es más pesada o más liviana?
Etiquete las monedas como 1, 2, 3, 4 y G (genuinas). Ahora tenemos algo de información sobre la pureza de las monedas. Necesitamos hacer uso de eso en las agrupaciones.
Podemos agruparlos mejor como [(G1, 23) y (4)]. Cualquier otro grupo no puede generar un árbol completo de 3 arios, pruébelo usted mismo. El siguiente diagrama explica el procedimiento.
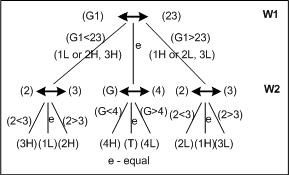
El caso medio (G1) = (23) se explica por sí mismo, es decir, 1, 2, 3 son genuinas y la 4ª moneda puede resultar más ligera o más pesada en una prueba más.
El lado izquierdo del árbol corresponde al caso (G1) < (23). Esto es posible de dos maneras, 1 debería ser más ligero o cualquiera de (2, 3) debería ser más pesado. El primer caso es obvio cuando se equilibra el próximo pesaje (2, 3), dando como resultado 1 más ligero. La última instancia podría ser (2) < (3) dando como resultado 3 más pesado o (2) > (3) dando como resultado 2 más pesado. Los Nodes de hoja en la rama izquierda se nombran para reflejar estos resultados.
El lado derecho del árbol corresponde al caso (G1) > (23). Esto es posible de dos maneras, 1 es más pesado o cualquiera de (2, 3) debería ser más ligero. El primer caso es obvio cuando se equilibra el siguiente pesaje (2, 3), dando como resultado 1 como más pesado. El último caso podría ser (2) < (3) dando 2 como moneda más ligera, o (2) > (3) dando 3 como moneda más ligera.
En el problema anterior, bajo cualquier posibilidad, solo necesitamos dos pesajes. Podemos utilizar todos los resultados de un árbol triario completo de dos niveles. Empezamos con (N + 1) = 5 monedas donde N = 4, terminamos con (2N + 1) = 9 hojas. De hecho, deberíamos tener 11 resultados ya que comenzamos con 5 monedas, ¿dónde están los otros 2 resultados? Estos dos resultados se pueden declarar en la raíz del árbol mismo (antes del primer pesaje), ¿puedes imaginar estos dos resultados?
Si observamos la figura, después del primer pesaje el problema se reduce a “sabemos tres monedas, o una puede ser más liviana (más pesada) o una entre otras dos puede ser más pesada (más liviana)”. Esto se puede resolver en un solo pesaje (lea el Problema 1).
Análisis: Dadas (N + 1) monedas, una es genuina y el resto N pueden ser genuinas o solo una moneda es defectuosa. El árbol de decisión requerido debe dar como resultado un mínimo de (2N + 1) hojas. Dado que los posibles resultados totales son (2(N + 1) + 1), el número de pesajes (ensayos) viene dado por la altura del árbol ternario, k >= log 3 [2(N + 1) + 1]. Tenga en cuenta el signo de igualdad .
Reorganizando k y N, podemos pesar un máximo de N <= (3 k – 3)/2 monedas en k intentos .
Problema 4: (El clásico rompecabezas de 12 monedas)
Se le da dos equilibrio justo pan. Tienes 12 monedas idénticas, de las cuales una moneda puede ser más liviana o más pesada. ¿Cómo puede encontrar monedas impares, si las hay, en pruebas mínimas, y también determinar si la moneda defectuosa es más liviana o más pesada, en el peor de los casos?
¿Cómo quieres agruparlos? ¿Biset o triset? Claramente podemos descartar la opción de dividir en dos grupos iguales. No puede conducir al mejor árbol. A partir de los dos ejemplos anteriores, podemos asegurar que el árbol de decisión se puede usar de manera óptima si podemos revelar al menos una moneda genuina . Recuerde agrupar las monedas de manera que el primer pesaje revele al menos una moneda genuina.
Llamemos a las monedas 1, 2, … 8, A, B, C y D. Podemos combinar las monedas en 3 grupos, a saber, (1234), (5678) y (ABCD). Pesar (1234) y (5678). Se le anima a dibujar un árbol de decisiones mientras lee el procedimiento. El resultado puede ser de tres maneras,
- (1234) = (5678), ambos grupos son iguales. La moneda defectuosa puede estar en el grupo (ABCD).
- (1234) < (5678), es decir, el primer grupo tiene menos peso que el segundo grupo.
- (1234) > (5678), es decir, el primer grupo tiene más peso que el segundo grupo.
La salida (1) puede resolverse en dos pesajes más como caso especial de balanza de dos platillos dado en el Problema 3. Sabemos que los grupos (1234) y (5678) son monedas genuinas y defectuosas que pueden estar en (ABCD). Elija una moneda genuina de cualquiera de los grupos pesados y proceda con (ABCD) como se explica en el Problema 3.
Los resultados (2) y (3) son especiales. En ambos casos, sabemos que (ABCD) es genuino. Y también, sabemos que un conjunto de monedas es más liviano y un conjunto de monedas más pesado. Necesitamos barajar los dos grupos pesados de tal manera que terminemos con un árbol de decisión de altura más pequeño.
Considere el segundo resultado donde() <(). Es posible cuando cualquier moneda entre (1, 2, 3, 4) es más ligera o cualquier moneda entre (5, 6, 7, 8) es más pesada. Revelamos una posibilidad más ligera o más pesada después del primer pesaje. Si procedemos como en el Problema 1, no generaremos el mejor árbol de decisión. Barajemos las monedas como() y (BCD) como nuevos grupos (hay diferentes barajados posibles, que también conducen a un peso mínimo). Si volvemos a pesar estos dos grupos, el resultado puede ser de tres maneras, i)() < (BCD) dando uno entre 1, 2, 3 es más ligero, similar al Problema 1 explicado anteriormente, necesitamos un pesaje más, ii) ( ) = (BCD) resultando uno entre 6, 7, 8 es más pesado, lo cual es similar al Problema 1 explicado anteriormente, necesitamos un peso más iii)() > (BCD) resultando 5 como moneda más pesada o 4 como moneda más liviana, en a expensas de un pesaje más.
De manera similar, también podemos resolver el subárbol derecho (tercer resultado donde() >()) en dos pesajes más.
Somos capaces de resolver el rompecabezas de 12 monedas en 3 pesajes en el peor de los casos.
Algunos rompecabezas interesantes:
- Resuelva el problema 4 con N = 8 y N = 13, ¿cuántas pruebas mínimas se requieren en cada caso?
- Dada una función int peso (A [], B []) donde A y B son arrays (no es necesario que tengan el mismo tamaño). La función devuelve -1, 0 o 1. Devuelve 0 si la suma de todos los elementos en A y B son iguales, -1 si A < B y 1 si A > B. Dada una array de 12 elementos, todos los elementos son iguales excepto una. El elemento impar puede ser como el de otros, más pequeño o más grande que otros. Escriba un programa para encontrar el elemento impar (si lo hay) usando el número mínimo de veces de weight() .
- Es posible que haya visto una balanza de 3 platos en los laboratorios de ciencias durante los días escolares. Dada una balanza de 3 platillos (4 resultados) y N monedas, ¿cuántas pruebas mínimas se necesitan para encontrar una moneda impar?
Referencias:
Se proporcionó un problema similar en uno de los ejercicios del libro «Introducción a los algoritmos de Levitin». Lea específicamente la sección 5.5 y la sección 11.2, incluidos los ejercicios.
– – – por . Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA