Requisito previo: máquina de Turing , máquina de Turing para sustracción | Conjunto 1
Un número se representa en formato binario en diferentes autómatas finitos como 5 se representa como (101) pero en caso de resta se sigue el formato unario de la Máquina de Turing. En formato unario, un número se representa ya sea por ceros o por unos.
Por ejemplo, 5 estará representado por una secuencia de cinco unos 5 = 1 1 1 1 1 o 0 0 0 0 0. Usemos ceros para la representación. Para la resta de números usando una máquina de Turing, ambos números se dan como entrada a la máquina de Turing separados por una «c».
Ejemplo: (3 – 4) o (4 – 3) se darán como 0 0 0 c 0 0 0 0
Input: 0 0 0 c 0 0 0 0 // (3 - 4) or (4 - 3) Output: 0 // (1)
Enfoque utilizado:
convierta un 0 en el primer número en X y luego muévase hacia la derecha, siga ignorando los 0 y la «c», luego convierta el primer 0 en X y muévase hacia la izquierda. Ahora sigue ignorando los 0, X y «c» y después de encontrar el segundo cero repite el mismo procedimiento hasta que todos los ceros del lado izquierdo se conviertan en X. Ahora muévete a la derecha y convierte la última X encontrada en B (en blanco).
Pasos –
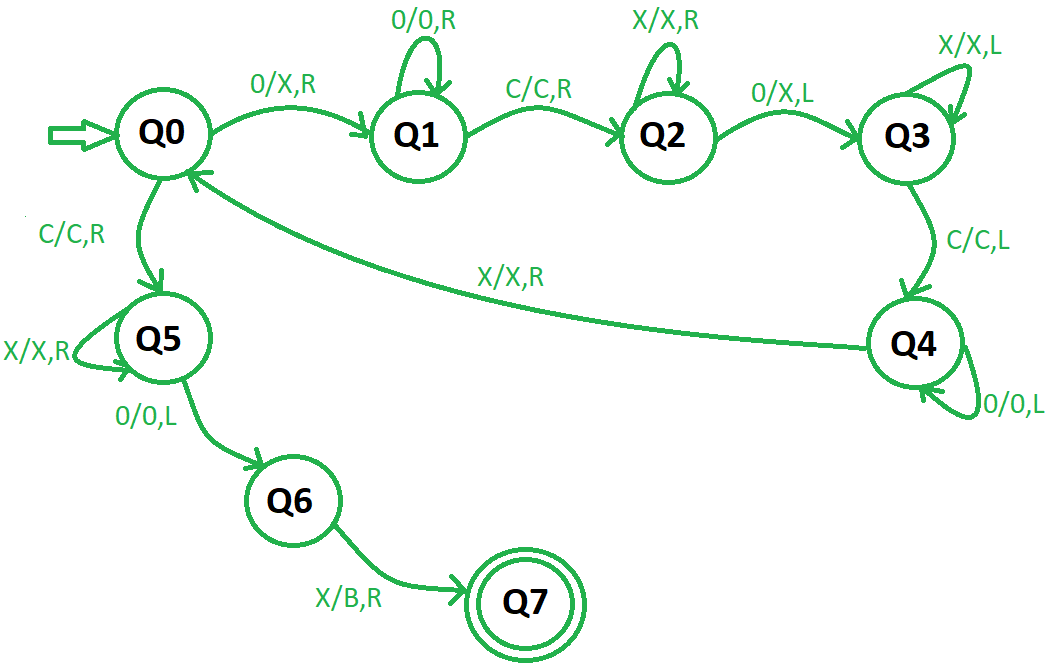
Paso 1: convierta 0 en X y muévase a la derecha, luego vaya al paso 2. Si el símbolo es «c», ignórelo moviéndose hacia la derecha y vaya al paso 6.
Paso 2: sigue ignorando los 0 y muévete a la derecha. Ignore «c», muévase a la derecha y vaya al paso 3.
Paso 3: sigue ignorando X y muévete a la derecha. Convierta el primer 0 encontrado como X y muévase hacia la izquierda y vaya al paso 4.
Paso 4: siga ignorando todas las X y «c» a la izquierda y vaya al paso 5.
Paso 5: siga moviéndose hacia la izquierda ignorando los 0 y cuando encuentre la primera X, ignórela y muévase hacia la derecha, y vaya al paso 1.
Paso 6: siga ignorando todas las X y muévase hacia la derecha. Ignore el primer 0 encontrado y muévase hacia la izquierda y luego vaya al paso 7.
Paso 7 –Convierta la X en B ( en blanco ) y vaya al paso 8 .
Paso 8 – Fin.
Publicación traducida automáticamente
Artículo escrito por Abhansh_gfg y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA