Un codificador es un circuito combinacional que realiza la operación inversa del decodificador. Tiene un máximo de 2^n líneas de entrada y ‘n’ líneas de salida , por lo que codifica la información de 2^n entradas en un código de n bits. Producirá un código binario equivalente a la entrada, que es alta activa. Por lo tanto, el codificador codifica 2^n líneas de entrada con ‘n’ bits.

Codificador 4 : 2 –
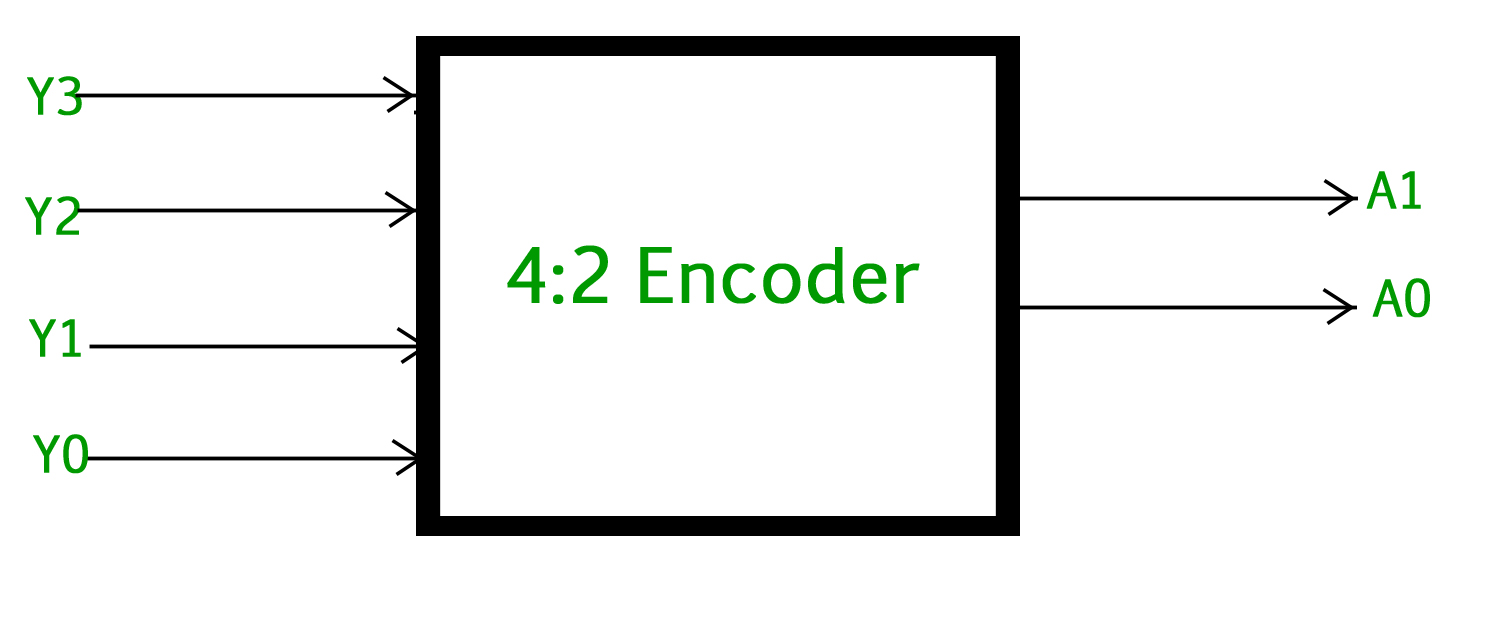
El codificador 4 a 2 consta de cuatro entradas Y3, Y2, Y1 e Y0 y dos salidas A1 y A0 . En cualquier momento, solo una de estas 4 entradas puede ser ‘1’ para obtener el código binario respectivo en la salida. La siguiente figura muestra el símbolo lógico del codificador 4 a 2:
La tabla de verdad del codificador 4 a 2 es la siguiente:

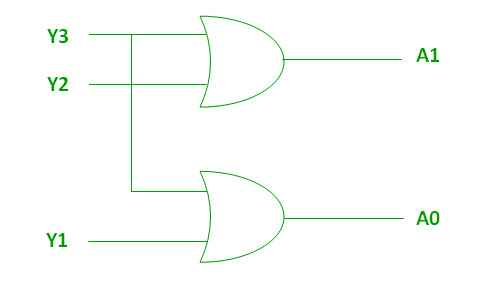
Expresión lógica para A1 y A0:
A1 = Y3 + Y2 A0 = Y3 + Y1
Las dos funciones booleanas anteriores A1 y A0 se pueden implementar utilizando dos puertas OR de entrada:
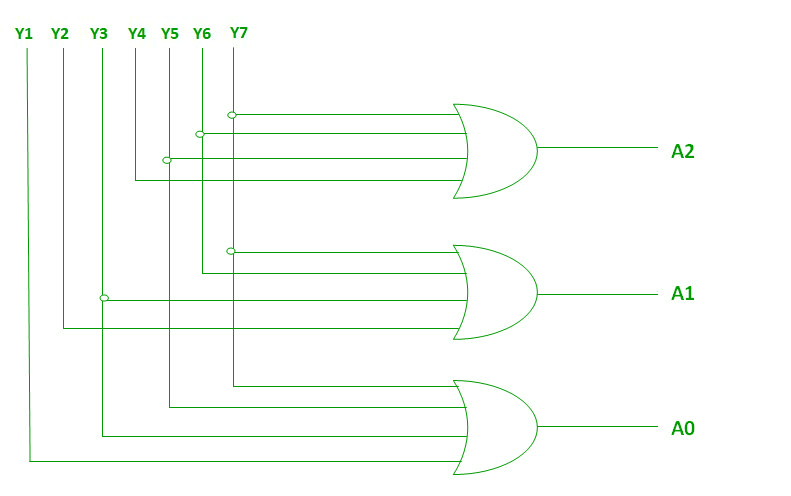
Codificador 8 : 3 (de octal a binario) –
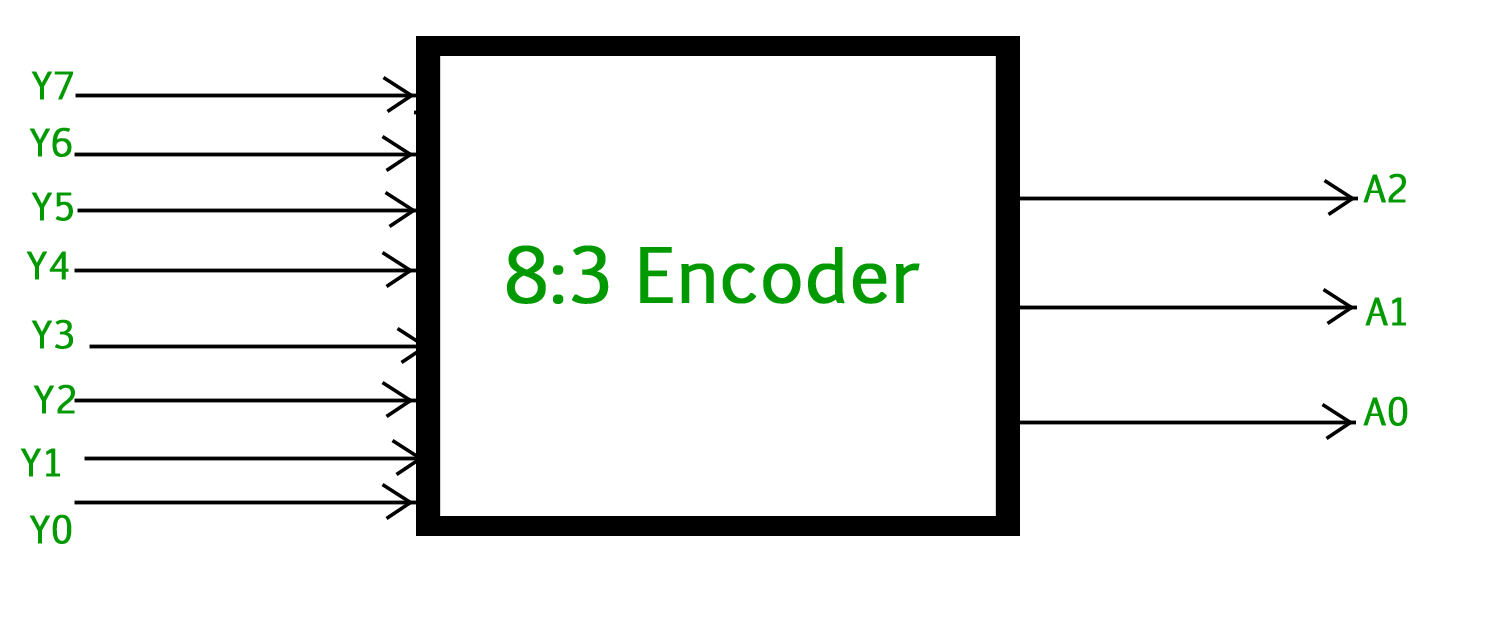
El codificador de 8 a 3 u octal a binario consta de 8 entradas : Y7 a Y0 y 3 salidas : A2, A1 y A0. Cada línea de entrada corresponde a cada dígito octal y tres salidas generan el código binario correspondiente.
La siguiente figura muestra el símbolo lógico del codificador octal a binario:
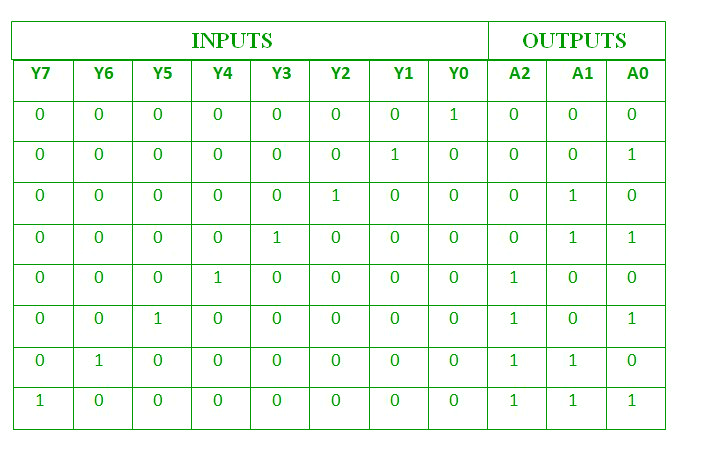
La tabla de verdad para el codificador 8 a 3 es la siguiente:
Expresión lógica para A2, A1 y A0:
A2 = Y7 + Y6 + Y5 + Y4 A1 = Y7 + Y6 + Y3 + Y2 A0 = Y7 + Y5 + Y3 + Y1
Las dos funciones booleanas anteriores A2, A1 y A0 se pueden implementar utilizando cuatro puertas OR de entrada:
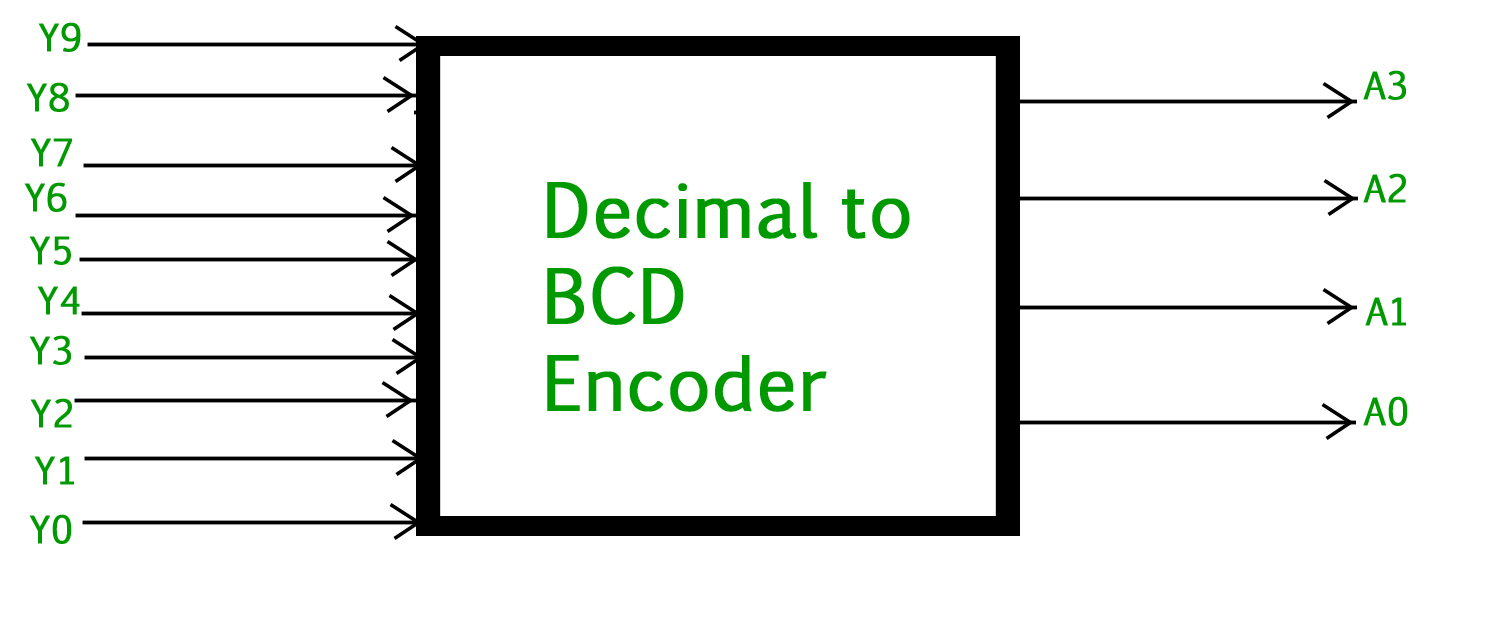
Decimal a codificador BCD –
El codificador de decimal a binario generalmente consta de 10 líneas de entrada y 4 líneas de salida . Cada línea de entrada corresponde a cada dígito decimal y 4 salidas corresponden al código BCD. Este codificador acepta los datos decimales decodificados como entrada y los codifica en la salida BCD que está disponible en las líneas de salida. La siguiente figura muestra el símbolo lógico del codificador decimal a BCD:
La tabla de verdad para el codificador decimal a BCD es la siguiente:

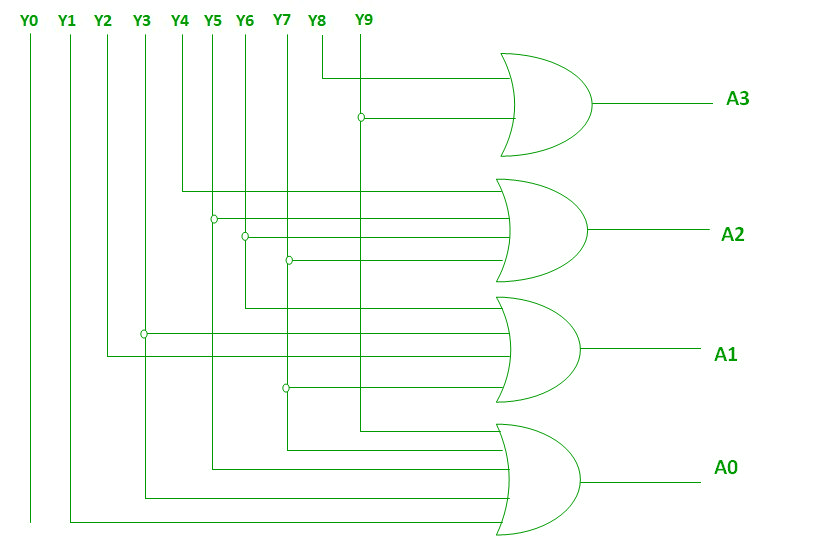
Expresión lógica para A3, A2, A1 y A0:
A3 = Y9 + Y8 A2 = Y7 + Y6 + Y5 +Y4 A1 = Y7 + Y6 + Y3 +Y2 A0 = Y9 + Y7 +Y5 +Y3 + Y1
Las dos funciones booleanas anteriores se pueden implementar usando puertas OR:
Codificador de prioridad –
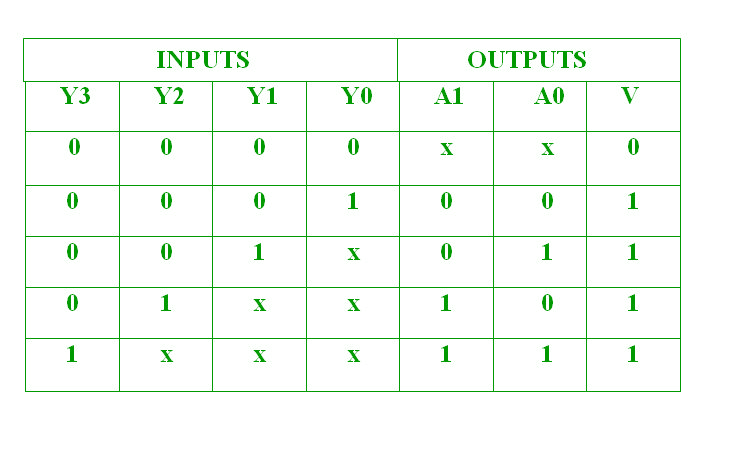
Un codificador de prioridad 4 a 2 tiene 4 entradas : Y3, Y2, Y1 e Y0 y 2 salidas : A1 y A0. Aquí, la entrada Y3 tiene la prioridad más alta , mientras que la entrada Y0 tiene la prioridad más baja . En este caso, incluso si más de una entrada es ‘1’ al mismo tiempo, la salida será el código (binario) correspondiente a la entrada que tiene mayor prioridad .
La tabla de verdad para el codificador de prioridad es la siguiente:
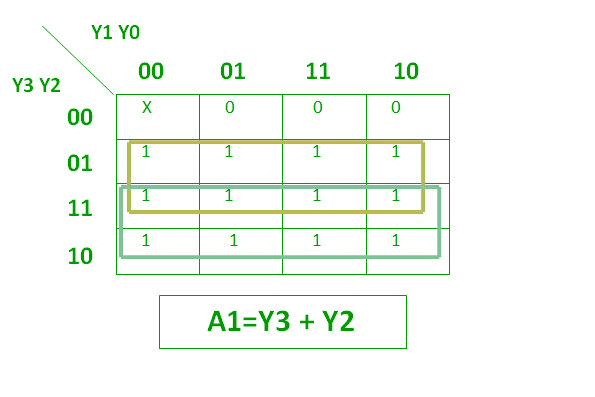
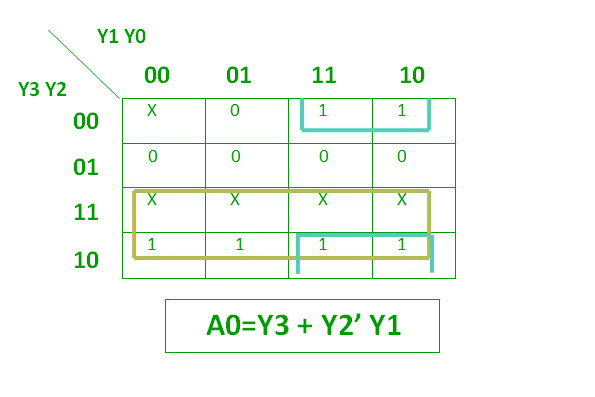
Las dos funciones booleanas anteriores se pueden implementar como:
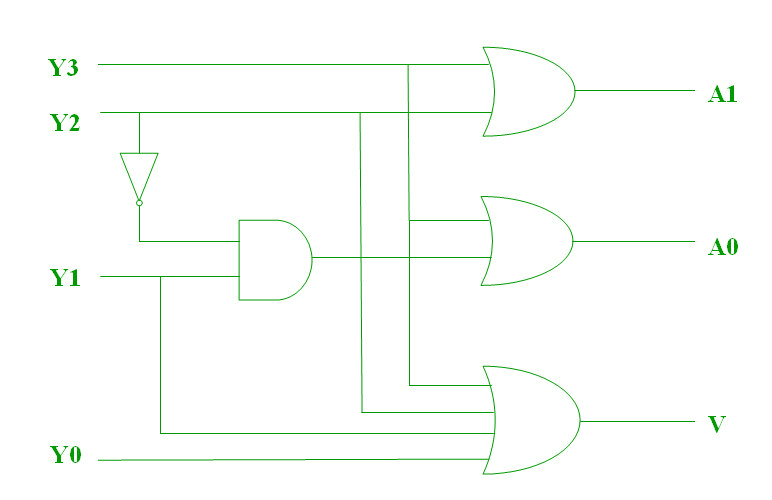
Inconvenientes de los codificadores normales:
- Hay una ambigüedad, cuando todas las salidas del codificador son iguales a cero.
- Si más de una entrada está activa en Alto, entonces el codificador produce una salida, que puede no ser el código correcto.
Entonces, para superar estas dificultades, debemos asignar prioridades a cada entrada del codificador. Entonces, la salida del codificador será el (código correspondiente a las entradas Altas activas, que tiene mayor prioridad.
Usos de codificadores –
- Los codificadores son circuitos electrónicos muy comunes utilizados en todos los sistemas digitales.
- Los codificadores se utilizan para traducir los valores decimales a binario para realizar funciones binarias como suma, resta, multiplicación, etc.
- Otras aplicaciones, especialmente para codificadores prioritarios, pueden incluir la detección de interrupciones en aplicaciones de microprocesador.
Preguntas de GATE CS Corner
Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.
Referencias –
Codificador – Wikipedia
Codificador de prioridad – Wikipedia
Este artículo es una contribución de Harshita Pandey . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA