Algoritmo RSA que utiliza una biblioteca aritmética de precisión múltiple

La criptografía de clave pública, también conocida como criptografía asimétrica, es el tipo de criptografía que implica el uso de dos claves, a saber, clave pública y clave privada. La clave pública del receptor se usa para cifrar el texto sin formato por el remitente, mientras que la clave privada del receptor se usa para descifrar el mensaje cifrado y, por lo tanto, solo puede ser descifrado por el receptor previsto.
RSA (Rivest Shamir Adleman) es un algoritmo criptográfico de clave pública en el que la generación de claves se basa en el producto de dos grandes números primos p y q que dan como resultado N, es decir, N = p × q. El quid de la seguridad de este algoritmo es que el atacante primero debe averiguar p y q mediante la factorización de N, que tiene lugar en un tiempo exponencial. La investigación muestra que esto puede tomar más de 70 años si N es un número de 100 dígitos. Debido a esta complejidad, el atacante no puede encontrar la clave de descifrado d porque d depende de p, q y la clave de cifrado e. Entonces, incluso si el atacante conoce N y e, no se puede calcular d.

Escenario actual de RSA:
a partir de abril de 2017, es posible que RSA-2048 no se pueda factorizar durante muchos años. Además, el reciente virus Ransomware también usa RSA-2048 para cifrar archivos en el sistema infectado. Estos archivos no se pueden descifrar sin la disponibilidad de la clave de descifrado porque una clave tan grande no se puede factorizar. Por lo tanto, RSA-1024 y RSA-2048 ahora se usan popularmente para comunicaciones seguras. 

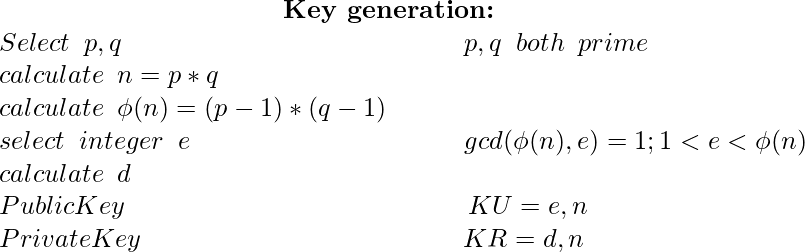
Las imágenes de arriba muestran las 3 fases diferentes del algoritmo RSA. Considerando que un generador de números primos genera números primos p y q de 1024 bits, la N resultante será un número de 2048 bits. Dado que todas las operaciones de módulo realizadas durante el cifrado y descifrado son con respecto a N, que es un número de 2048 bits, la implementación del software puede llevar mucho tiempo. Además, el tipo de datos long long int sin signo de C restringe los cálculos a números de 64 bits. Para respaldar la generación de claves de gran tamaño como requisito del algoritmo RSA y el cálculo rápido de cifrado y descifrado que implica un módulo de gran tamaño, se puede utilizar una biblioteca llamada GMP (GNU Multiple Precision Arithmetic Library).
 

¿Qué es GMP?
GMP es una biblioteca de código abierto que permite realizar cálculos aritméticos en enteros con signo, números racionales y números decimales sin ninguna limitación práctica en su precisión, aparte de las configuraciones de la máquina en la que se ejecuta. Esta biblioteca se utiliza durante aquellos cálculos aritméticos que involucran números muy grandes o de alta precisión, la mayoría de los cuales se utilizan en algoritmos criptográficos. El beneficio de usar esta biblioteca es que brinda soporte para números de precisión arbitraria, cuyo tamaño no se conoce antes de la ejecución del programa. La interfaz básica proporcionada para el uso de esta biblioteca es para el lenguaje C. Pero existen envoltorios para otros lenguajes, incluidos Ada, C++, C#, Julia, OCaml, Perl, PHP, Python, R, Ruby y Wolfram Language.
A modo de ejemplo, a continuación se menciona un programa en C que realiza la multiplicación de dos números de precisión múltiple. 
Tenga en cuenta que el archivo gmp.h debe incluirse como un archivo de encabezado. La compilación de dicho programa en un sistema Unix se puede hacer usando el comando 
 

gcc program_name.c -lgmp

#include <stdio.h>
#include <gmp.h>
 
int main(void) {
   mpz_t x, y, result;
 
   mpz_init_set_str(x, "7612058254738945", 10);
   mpz_init_set_str(y, "9263591128439081", 10);
   mpz_init(result);
 
   mpz_mul(result, x, y);
   gmp_printf("    %Zd\n"
              "*\n"
              "    %Zd\n"
              "--------------------\n"
              "%Zd\n", x, y, result);
 
   /* free used memory */
   mpz_clear(x);
   mpz_clear(y);
   mpz_clear(result);
   
   return 0;
}

Codificación del algoritmo RSA:
El programa AC que describe el funcionamiento del algoritmo RSA con números primos pequeños está disponible aquí . Para comprender el funcionamiento del algoritmo RSA real con el uso de números primos grandes, aquí está disponible un código C que utiliza la biblioteca GMP . Este programa implementa RSA-1024 mediante la generación de números primos aleatorios p y q de 512 bits cada uno, seguidos de cifrado y descifrado. Aquí, a la variable MODULUS_SIZE se le asigna el valor 1024. Este valor se puede cambiar a 2048 para generar claves RSA de 2048 bits. 
 

Aplicaciones: el
algoritmo RSA se ha utilizado ampliamente en comunicaciones de red seguras y transacciones seguras para muchas aplicaciones de comercio electrónico. Otras aplicaciones incluyen la comunicación de voz a través de canales de baja tasa de bits, en el intercambio seguro de claves incluso para IPSec de alta velocidad, detalles de tarjetas de crédito cuando se comunican a comerciantes en línea, etc.