Organización Informática | Algoritmo de Booth

El algoritmo de Booth brinda un procedimiento para multiplicar enteros binarios en representación de complemento a 2 con signo de manera eficiente , es decir, se requiere menos número de sumas/restas. Opera en el hecho de que las strings de 0 en el multiplicador no requieren adición sino solo desplazamiento y una string de 1 en el multiplicador desde el peso de bit 2^k hasta el peso de 2^m puede tratarse como 2^(k+1) a 2 ^ m. Como en todos los esquemas de multiplicación, el algoritmo de cabina requiere el examen de los bits del multiplicador y el desplazamiento del producto parcial. Antes del cambio, el multiplicando puede sumarse al producto parcial, restarse del producto parcial o dejarse sin cambios de acuerdo con las siguientes reglas:

1. El multiplicando se resta del producto parcial al encontrar el primer 1 menos significativo en una string de 1 en el multiplicador.
2. El multiplicando se agrega al producto parcial al encontrar el primer 0 (siempre que haya un ‘1’ anterior) en una string de 0 en el multiplicador.
3. El producto parcial no cambia cuando el bit multiplicador es idéntico al bit multiplicador anterior.

Implementación de hardware del algoritmo de cabinas: la implementación de hardware del algoritmo de cabina requiere la configuración de registro que se muestra en la siguiente figura.

Diagrama de flujo del algoritmo de Booth: nombramos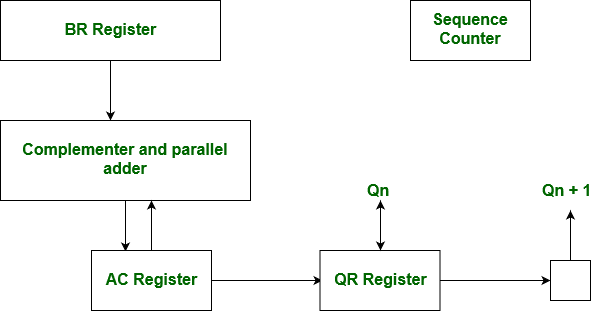 el registro como A, B y Q, AC, BR y QR respectivamente. Qn designa el bit menos significativo del multiplicador en el registro QR. Se agrega un flip-flop adicional Qn+1 a QR para facilitar una doble inspección del multiplicador. El diagrama de flujo para el algoritmo de cabina se muestra a continuación. 

 AC y el bit adjunto Qn+1 se borran inicialmente a 0 y la secuencia SC se establece en un número n igual al número de bits en el multiplicador. Se inspeccionan los dos bits del multiplicador en Qn y Qn+1. Si los dos bits son iguales a 10, significa que se ha encontrado el primer 1 de una string. Esto requiere restar el multiplicando del producto parcial en AC. Si los 2 bits son iguales a 01, significa que se ha encontrado el primer 0 en una string de 0. Esto requiere la suma del multiplicando al producto parcial en AC. Cuando los dos bits son iguales, el producto parcial no cambia. No puede ocurrir un desbordamiento porque la suma y la resta del multiplicando se suceden. Como consecuencia, los 2 números que se suman siempre tienen signos opuestos, condición que excluye un desbordamiento. El siguiente paso es desplazar a la derecha el producto parcial y el multiplicador (incluido Qn+1). Esta es una operación de desplazamiento aritmético a la derecha (ashr) en la que AC y QR giran a la derecha y no modifican el bit de signo en AC. El contador de secuencias se decrementa y el bucle computacional se repite n veces.Ejemplo: a continuación se muestra un ejemplo numérico del algoritmo de Booth para n = 4. Muestra la multiplicación paso a paso de -5 y -7.

BR = -5 = 1011, BR' = 0100, BR'+1 = 0101
QR = -7 = 1001 
The explanation of first step is as follows: Qn+1                             
AC = 0000, QR = 1001, Qn+1 = 0,  SC = 4   
Qn Qn+1 = 10    
So, we do AC + (BR)'+1, which gives AC = 0101
On right shifting AC and QR, we get
AC = 0010, QR = 1100 and Qn+1 = 1 

OPERACIÓN	C.A.	código QR	Qn+1	CAROLINA DEL SUR
	0000	1001	0	4
CA + BR’ + 1	0101	1001	0
ASHR	0010	1100	1	3
CA + BR	1101	1100	1
ASHR	1110	1110	0	2
ASHR	1111	0111	0	1
CA + BR’ + 1	0010	0011	1	0

El producto se calcula de la siguiente manera:

Product = AC QR
Product = 0010 0011 =  35

Ocurrencia en el mejor y el peor de los casos: El mejor caso es cuando hay un gran bloque de 1 y 0 consecutivos en los multiplicadores, de modo que hay un número mínimo de operaciones lógicas, como sumas y restas. El peor de los casos es cuando hay pares de 0 y 1 alternos, ya sea 01 o 10 en los multiplicadores, por lo que se requiere el número máximo de sumas y restas. Preguntas de práctica GATE –

1. PUERTA 2008 | Pregunta 40
2. PUERTA 2006 | Pregunta 38
3. PUERTA 2005 | Pregunta 8
4. PUERTA CS 1996 | Pregunta 23