¿Por qué necesitamos un algoritmo de compresión?
Hay dos categorías de técnicas de compresión, con pérdida y sin pérdida. Si bien cada uno usa diferentes técnicas para comprimir archivos, ambos tienen el mismo objetivo: buscar datos duplicados en el gráfico (GIF para LZW) y usar una representación de datos mucho más compacta. La compresión sin pérdidas reduce los bits al identificar y eliminar la redundancia estadística. No se pierde información en la compresión sin pérdidas. Por otro lado, la compresión con pérdida reduce los bits al eliminar información innecesaria o menos importante. Entonces necesitamos Compresión de Datos principalmente porque:
- Los datos sin comprimir pueden ocupar mucho espacio, lo que no es bueno para el espacio limitado en el disco duro y las velocidades de descarga de Internet.
- Si bien el hardware mejora y se abarata, los algoritmos para reducir el tamaño de los datos también ayudan a que la tecnología evolucione.
- Ejemplo: un minuto de video HD sin comprimir puede ocupar más de 1 GB. ¿Cómo podemos meter una película de dos horas en un disco Blu-ray de 25 GB?
Los métodos de compresión con pérdida incluyen DCT (transformada de coseno discreta), cuantificación vectorial y codificación de transformación, mientras que los métodos de compresión sin pérdida incluyen RLE (codificación de longitud de ejecución), compresión de tabla de strings, LZW (Lempel Ziff Welch) y zlib. Existen varios algoritmos de compresión, pero nos estamos concentrando en LZW.
¿Qué es el algoritmo Lempel-Ziv-Welch (LZW)?
El algoritmo LZW es una técnica de compresión muy común. Este algoritmo se usa normalmente en GIF y, opcionalmente, en PDF y TIFF. El comando ‘comprimir’ de Unix, entre otros usos. No tiene pérdidas, lo que significa que no se pierden datos al comprimir. El algoritmo es simple de implementar y tiene el potencial de un rendimiento muy alto en las implementaciones de hardware. Es el algoritmo de la utilidad de compresión de archivos Unix ampliamente utilizada compress y se utiliza en el formato de imagen GIF.
La Idea se basa en patrones recurrentes para ahorrar espacio de datos. LZW es la técnica más importante para la compresión de datos de propósito general debido a su simplicidad y versatilidad. Es la base de muchas utilidades para PC que pretenden “duplicar la capacidad de tu disco duro”.
¿Como funciona?
La compresión LZW funciona leyendo una secuencia de símbolos, agrupando los símbolos en strings y convirtiendo las strings en códigos. Debido a que los códigos ocupan menos espacio que las strings que reemplazan, obtenemos compresión. Las características características de LZW incluyen,
- La compresión LZW utiliza una tabla de códigos, con 4096 como opción común para el número de entradas de la tabla. Los códigos 0-255 en la tabla de códigos siempre se asignan para representar bytes individuales del archivo de entrada.
- Cuando comienza la codificación, la tabla de códigos contiene solo las primeras 256 entradas, y el resto de la tabla está en blanco. La compresión se logra usando los códigos 256 a 4095 para representar secuencias de bytes.
- A medida que continúa la codificación, LZW identifica secuencias repetidas en los datos y las agrega a la tabla de códigos.
- La decodificación se logra tomando cada código del archivo comprimido y traduciéndolo a través de la tabla de códigos para encontrar qué carácter o caracteres representa.
Ejemplo: código ASCII. Por lo general, cada carácter se almacena con 8 bits binarios, lo que permite hasta 256 símbolos únicos para los datos. Este algoritmo intenta ampliar la biblioteca de 9 a 12 bits por carácter. Los nuevos símbolos únicos se componen de combinaciones de símbolos que ocurrieron previamente en la string. No siempre se comprime bien, especialmente con cuerdas cortas y diversas. Pero es bueno para comprimir datos redundantes y no tiene que guardar el nuevo diccionario con los datos: este método puede comprimir y descomprimir datos.
Ya hay excelentes artículos escritos, puede ver más en profundidad aquí , y también el artículo de Mark Nelson es digno de elogio.
Implementación
La idea del algoritmo de compresión es la siguiente: a medida que se procesan los datos de entrada, un diccionario mantiene una correspondencia entre las palabras más largas encontradas y una lista de valores de código. Las palabras se reemplazan por sus códigos correspondientes y así se comprime el archivo de entrada. Por lo tanto, la eficiencia del algoritmo aumenta a medida que aumenta el número de palabras largas y repetitivas en los datos de entrada.
CODIFICACIÓN LZW
* PSEUDOCODE 1 Initialize table with single character strings 2 P = first input character 3 WHILE not end of input stream 4 C = next input character 5 IF P + C is in the string table 6 P = P + C 7 ELSE 8 output the code for P 9 add P + C to the string table 10 P = C 11 END WHILE 12 output code for P
Probando el código a continuación:
Producción :

Además, verifique el código convertido por Mark Nelson al estilo C++. Hay otra variación de 6 versiones diferentes aquí . Además, Rosettacode enumera varias implementaciones de LZW en diferentes idiomas.
Compresión usando LZW
Ejemplo 1: Use el algoritmo LZW para comprimir la string: BABAABAAA
Los pasos involucrados se muestran sistemáticamente en el siguiente diagrama.
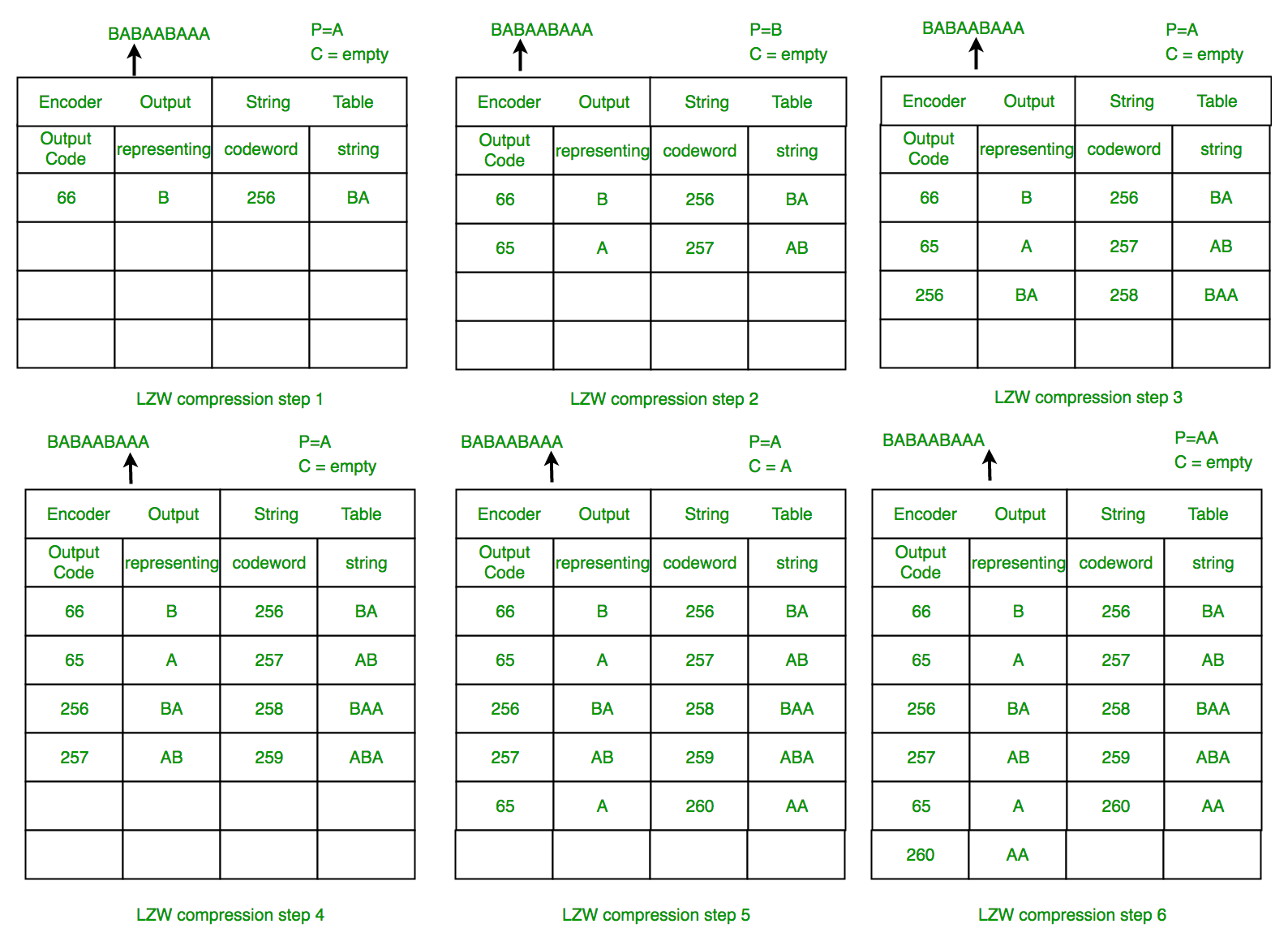
Descompresión LZW
El descompresor LZW crea la misma tabla de strings durante la descompresión. Comienza con las primeras 256 entradas de la tabla inicializadas en caracteres individuales. La tabla de strings se actualiza para cada carácter del flujo de entrada, excepto el primero. La decodificación se logra leyendo códigos y traduciéndolos a través de la tabla de códigos que se está construyendo.
Algoritmo de descompresión LZW
* PSEUDOCODE 1 Initialize table with single character strings 2 OLD = first input code 3 output translation of OLD 4 WHILE not end of input stream 5 NEW = next input code 6 IF NEW is not in the string table 7 S = translation of OLD 8 S = S + C 9 ELSE 10 S = translation of NEW 11 output S 12 C = first character of S 13 OLD + C to the string table 14 OLD = NEW 15 END WHILE
Ejemplo 2: Descompresión LZW: Use LZW para descomprimir la secuencia de salida de: <66><65><256><257><65><260>
Los pasos involucrados se muestran sistemáticamente en el siguiente diagrama.
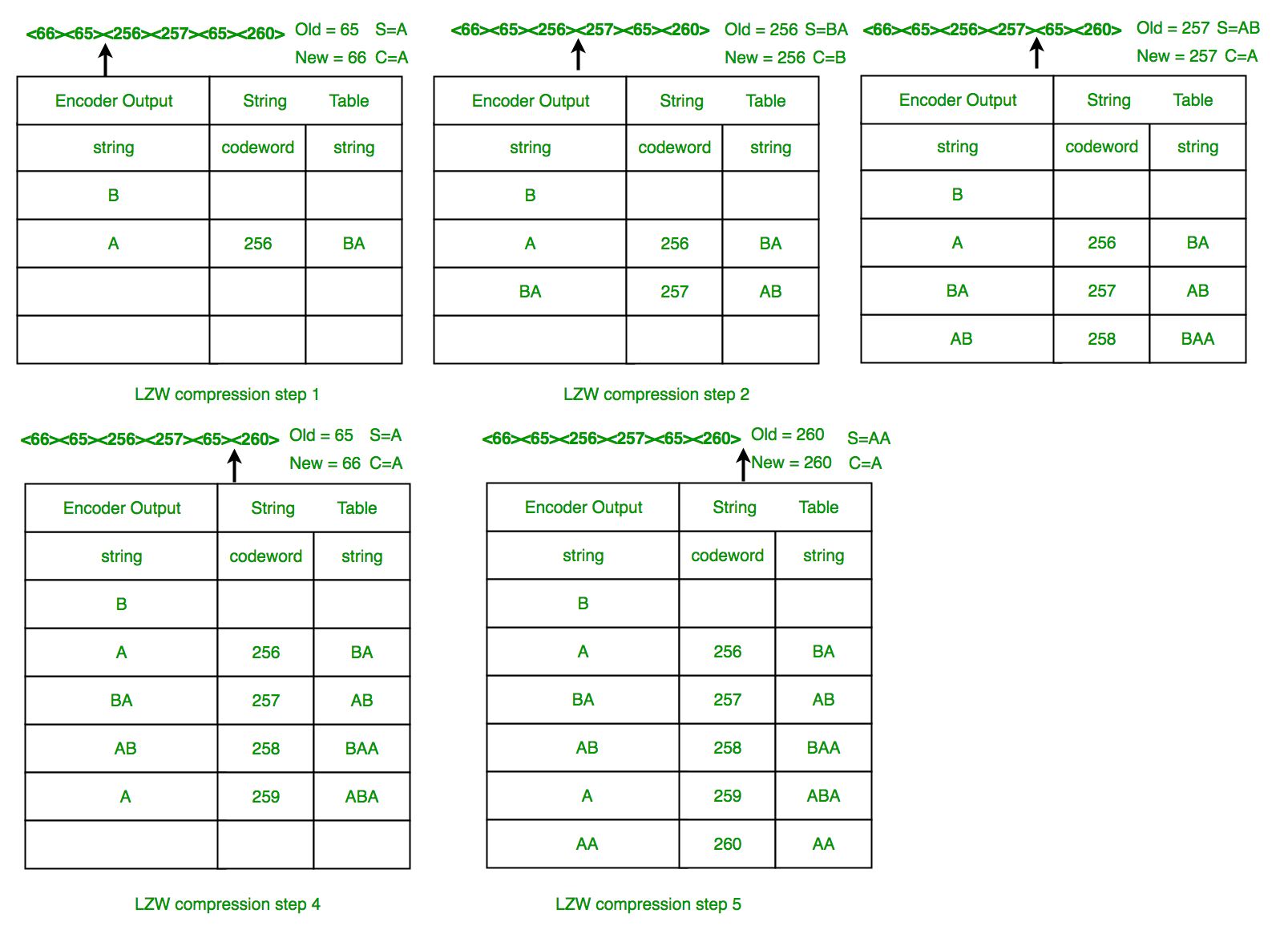
En este ejemplo, 72 bits se representan con 72 bits de datos. Después de construir una tabla de strings razonable, la compresión mejora drásticamente.
Resumen de LZW: este algoritmo comprime muy bien secuencias repetitivas de datos. Dado que las palabras de código son de 12 bits, cualquier carácter codificado único ampliará el tamaño de los datos en lugar de reducirlo.
A continuación se proporciona un código C++ para la compresión LZW tanto para la codificación como para la decodificación:
C++
#include <bits/stdc++.h>
using namespace std;
vector<int> encoding(string s1)
{
cout << "Encoding\n";
unordered_map<string, int> table;
for (int i = 0; i <= 255; i++) {
string ch = "";
ch += char(i);
table[ch] = i;
}
string p = "", c = "";
p += s1[0];
int code = 256;
vector<int> output_code;
cout << "String\tOutput_Code\tAddition\n";
for (int i = 0; i < s1.length(); i++) {
if (i != s1.length() - 1)
c += s1[i + 1];
if (table.find(p + c) != table.end()) {
p = p + c;
}
else {
cout << p << "\t" << table[p] << "\t\t"
<< p + c << "\t" << code << endl;
output_code.push_back(table[p]);
table[p + c] = code;
code++;
p = c;
}
c = "";
}
cout << p << "\t" << table[p] << endl;
output_code.push_back(table[p]);
return output_code;
}
void decoding(vector<int> op)
{
cout << "\nDecoding\n";
unordered_map<int, string> table;
for (int i = 0; i <= 255; i++) {
string ch = "";
ch += char(i);
table[i] = ch;
}
int old = op[0], n;
string s = table[old];
string c = "";
c += s[0];
cout << s;
int count = 256;
for (int i = 0; i < op.size() - 1; i++) {
n = op[i + 1];
if (table.find(n) == table.end()) {
s = table[old];
s = s + c;
}
else {
s = table[n];
}
cout << s;
c = "";
c += s[0];
table[count] = table[old] + c;
count++;
old = n;
}
}
int main()
{
string s = "WYS*WYGWYS*WYSWYSG";
vector<int> output_code = encoding(s);
cout << "Output Codes are: ";
for (int i = 0; i < output_code.size(); i++) {
cout << output_code[i] << " ";
}
cout << endl;
decoding(output_code);
}
Encoding String Output_Code Addition W 87 WY 256 Y 89 YS 257 S 83 S* 258 * 42 *W 259 WY 256 WYG 260 G 71 GW 261 WY 256 WYS 262 S* 258 S*W 263 WYS 262 WYSW 264 WYS 262 WYSG 265 G 71 Output Codes are: 87 89 83 42 256 71 256 258 262 262 71 Decoding WYS*WYGWYS*WYSWYSG
Ventajas de LZW sobre Huffman :
- LZW no requiere información previa sobre el flujo de datos de entrada.
- LZW puede comprimir el flujo de entrada en un solo paso.
- Otra ventaja de LZW es su simplicidad, lo que permite una ejecución rápida.
Recursos:
- mit.edu
- Dave.Marshall
- duque.edu
- michael.dipperstein
- LZW (YouTube)
- facultad.kfupm.edu.sa
- repositorio de github (kmeelu)
Este artículo es una contribución de Amartya Ranjan Saikia . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
