Hemos estado escribiendo sobre algoritmos eficientes para resolver problemas complejos, como la ruta más corta , el gráfico de Euler , el árbol de expansión mínimo , etc. Todas esas fueron historias de éxito de diseñadores de algoritmos. En esta publicación, se discuten las historias de fallas de la informática.
¿Todos los problemas computacionales pueden ser resueltos por una computadora? Hay problemas computacionales que no pueden ser resueltos por algoritmos incluso con tiempo ilimitado. Por ejemplo, el problema de detención de Turing (dado un programa y una entrada, si el programa finalmente se detendrá cuando se ejecute con esa entrada o se ejecutará para siempre). Alan Turing demostró que no puede existir un algoritmo general para resolver el problema de detención para todos los pares posibles de entrada de programa. Una parte clave de la prueba es que la máquina de Turing se usó como una definición matemática de una computadora y un programa ( problema de interrupción de la fuente ).
El estado de los problemas NP-Completos es otra historia de fallas, los problemas NP-completos son problemas cuyo estado se desconoce. Todavía no se ha descubierto ningún algoritmo de tiempo polinomial para ningún problema NP-completo, ni nadie ha podido probar que no exista ningún algoritmo de tiempo polinomial para ninguno de ellos. La parte interesante es que si cualquiera de los problemas NP-completos se puede resolver en tiempo polinomial, entonces se pueden resolver todos.
¿Qué son los problemas , y ? es un conjunto de problemas que pueden resolverse mediante una máquina de Turing determinista en tiempo polinomial.
es un conjunto de problemas de decisión que pueden resolverse mediante una máquina de Turing no determinista en tiempo polinomial. P es un subconjunto de NP (cualquier problema que pueda ser resuelto por una máquina determinista en tiempo polinomial también puede ser resuelto por una máquina no determinista en tiempo polinomial).
De manera informal, NP es un conjunto de problemas de decisión que se pueden resolver mediante un tiempo polinomial a través de un «Algoritmo de la suerte», un algoritmo mágico que siempre hace una suposición correcta entre el conjunto de opciones dado ( Referencia de fuente 1 ).
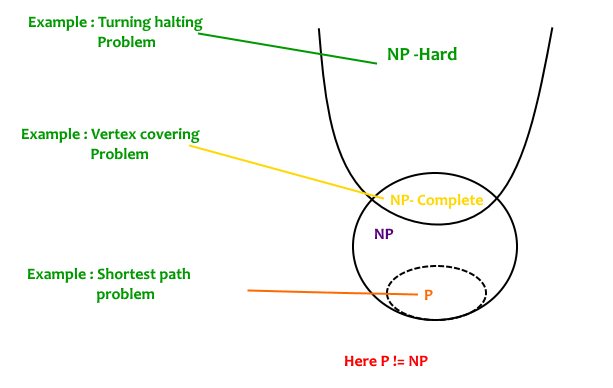
Los problemas son los problemas más difíciles del conjunto. Un problema de decisión L es NP-completo si:
1) L está en NP (cualquier solución dada para problemas NP-completos se puede verificar rápidamente, pero no existe una solución eficiente conocida).
2) Todo problema en NP es reducible a L en tiempo polinómico (la reducción se define a continuación).
Un problema es si sigue la propiedad 2 mencionada anteriormente y no necesita seguir la propiedad 1. Por lo tanto, el conjunto NP-Completo también es un subconjunto del conjunto NP-Hard.
Problemas de decisión frente a problemas de optimización
La NP-completitud se aplica al ámbito de los problemas de decisión. Se configuró de esta manera porque es más fácil comparar la dificultad de los problemas de decisión que la de los problemas de optimización. En realidad, sin embargo, ser capaz de resolver un problema de decisión en tiempo polinomial a menudo nos permitirá resolver el problema de optimización correspondiente en tiempo polinomial (utilizando un número polinomial de llamadas al problema de decisión). Entonces, discutir la dificultad de los problemas de decisión a menudo es equivalente a discutir la dificultad de los problemas de optimización. ( Referencia de fuente 2 ).
Por ejemplo, considere el problema de la cobertura de vértices(Dado un gráfico, encuentre el conjunto de vértices de tamaño mínimo que cubre todos los bordes). Es un problema de optimización. El problema de decisión correspondiente es, dado el gráfico no dirigido G y k, ¿hay una cubierta de vértice de tamaño k?
¿Qué es la reducción?
Sean L 1 y L 2 dos problemas de decisión. Supongamos que el algoritmo A 2 resuelve L 2 . Es decir, si y es una entrada para L 2 , entonces el algoritmo A 2 responderá Sí o No dependiendo de si y pertenece a L 2 o no.
La idea es encontrar una transformación de L 1 a L 2 para que el algoritmo A 2 pueda ser parte de un algoritmo A 1 para resolver L 1 .

La reducción del aprendizaje, en general, es muy importante. Por ejemplo, si tenemos funciones de biblioteca para resolver determinados problemas y si podemos reducir un problema nuevo a uno de los problemas resueltos, ahorramos mucho tiempo. Considere el ejemplo de un problema en el que tenemos que encontrar la ruta de producto mínimo en un gráfico dirigido dado donde el producto de la ruta es la multiplicación de los pesos de los bordes a lo largo de la ruta. Si tenemos código para el algoritmo de Dijkstra para encontrar la ruta más corta, podemos tomar el registro de todos los pesos y usar el algoritmo de Dijkstra para encontrar la ruta mínima del producto en lugar de escribir un código nuevo para este nuevo problema.
¿Cómo probar que un problema dado es NP-completo?
A partir de la definición de NP-completo, parece imposible demostrar que un problema L es NP-Completo. Por definición, requiere que mostremos que cada problema en NP es tiempo polinomial reducible a L. Afortunadamente, hay una forma alternativa de demostrarlo. La idea es tomar un problema NP-Completo conocido y reducirlo a L. Si es posible una reducción de tiempo polinomial, podemos demostrar que L es NP-Completo por transitividad de reducción (Si un problema NP-Completo es reducible a L en tiempo polinomial, entonces todos los problemas son reducibles a L en tiempo polinomial).
¿Cuál fue el primer problema demostrado como NP-Complete?
Debe haber algún primer problema NP-Completo demostrado por la definición de problemas NP-Completos. SAT (problema booleano de satisfacibilidad) es el primer problema NP-Completo probado por Cook (consulte el libro CLRS para ver la prueba).
Siempre es útil saber acerca de NP-Completeness incluso para ingenieros. Suponga que se le pide que escriba un algoritmo eficiente para resolver un problema extremadamente importante para su empresa. Después de mucho pensar, solo puede encontrar un enfoque de tiempo exponencial que no es práctico. Si no sabe acerca de NP-Completeness, solo puede decir que no pude encontrar un algoritmo eficiente. Si sabe acerca de la completitud de NP y demuestra que el problema es NP-completo, puede decir con orgullo que es poco probable que exista la solución en tiempo polinomial. Si existe una solución de tiempo polinomial posible, entonces esa solución resuelve un gran problema de informática que muchos científicos han estado intentando durante años.
Pronto discutiremos más problemas de NP-Completo y su prueba de NP-Completo.
Referencias:
Conferencia en video del MIT sobre la complejidad computacional
Introducción a los algoritmos 3.ª edición por Clifford Stein, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest
http://www.ics.uci.edu/~eppstein/161/960312. html
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA