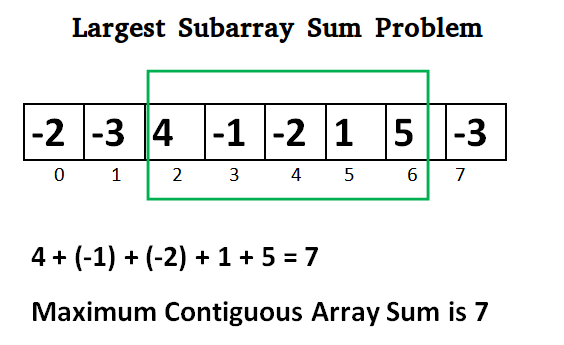
Escriba un programa eficiente para encontrar la suma del subarreglo contiguo dentro de un arreglo unidimensional de números que tenga la suma más grande.
C++
// C++ program to print largest contiguous array sum
#include<iostream>
#include<climits>
using namespace std;
int maxSubArraySum(int a[], int size)
{
int max_so_far = INT_MIN, max_ending_here = 0;
for (int i = 0; i < size; i++)
{
max_ending_here = max_ending_here + a[i];
if (max_so_far < max_ending_here)
max_so_far = max_ending_here;
if (max_ending_here < 0)
max_ending_here = 0;
}
return max_so_far;
}
/*Driver program to test maxSubArraySum*/
int main()
{
int a[] = {-2, -3, 4, -1, -2, 1, 5, -3};
int n = sizeof(a)/sizeof(a[0]);
int max_sum = maxSubArraySum(a, n);
cout << "Maximum contiguous sum is " << max_sum;
return 0;
}
Java
import java.io.*;
// Java program to print largest contiguous array sum
import java.util.*;
class Kadane
{
public static void main (String[] args)
{
int [] a = {-2, -3, 4, -1, -2, 1, 5, -3};
System.out.println("Maximum contiguous sum is " +
maxSubArraySum(a));
}
static int maxSubArraySum(int a[])
{
int size = a.length;
int max_so_far = Integer.MIN_VALUE, max_ending_here = 0;
for (int i = 0; i < size; i++)
{
max_ending_here = max_ending_here + a[i];
if (max_so_far < max_ending_here)
max_so_far = max_ending_here;
if (max_ending_here < 0)
max_ending_here = 0;
}
return max_so_far;
}
}
Python
# Python program to find maximum contiguous subarray # Function to find the maximum contiguous subarray from sys import maxint def maxSubArraySum(a,size): max_so_far = -maxint - 1 max_ending_here = 0 for i in range(0, size): max_ending_here = max_ending_here + a[i] if (max_so_far < max_ending_here): max_so_far = max_ending_here if max_ending_here < 0: max_ending_here = 0 return max_so_far # Driver function to check the above function a = [-2, -3, 4, -1, -2, 1, 5, -3] print "Maximum contiguous sum is", maxSubArraySum(a,len(a)) #This code is contributed by _Devesh Agrawal_
C#
// C# program to print largest
// contiguous array sum
using System;
class GFG
{
static int maxSubArraySum(int []a)
{
int size = a.Length;
int max_so_far = int.MinValue,
max_ending_here = 0;
for (int i = 0; i < size; i++)
{
max_ending_here = max_ending_here + a[i];
if (max_so_far < max_ending_here)
max_so_far = max_ending_here;
if (max_ending_here < 0)
max_ending_here = 0;
}
return max_so_far;
}
// Driver code
public static void Main ()
{
int [] a = {-2, -3, 4, -1, -2, 1, 5, -3};
Console.Write("Maximum contiguous sum is " +
maxSubArraySum(a));
}
}
// This code is contributed by Sam007_
PHP
<?php
// PHP program to print largest
// contiguous array sum
function maxSubArraySum($a, $size)
{
$max_so_far = PHP_INT_MIN;
$max_ending_here = 0;
for ($i = 0; $i < $size; $i++)
{
$max_ending_here = $max_ending_here + $a[$i];
if ($max_so_far < $max_ending_here)
$max_so_far = $max_ending_here;
if ($max_ending_here < 0)
$max_ending_here = 0;
}
return $max_so_far;
}
// Driver code
$a = array(-2, -3, 4, -1,
-2, 1, 5, -3);
$n = count($a);
$max_sum = maxSubArraySum($a, $n);
echo "Maximum contiguous sum is " ,
$max_sum;
// This code is contributed by anuj_67.
?>
Javascript
<script>
// JavaScript program to find maximum
// contiguous subarray
// Function to find the maximum
// contiguous subarray
function maxSubArraySum(a, size)
{
var maxint = Math.pow(2, 53)
var max_so_far = -maxint - 1
var max_ending_here = 0
for (var i = 0; i < size; i++)
{
max_ending_here = max_ending_here + a[i]
if (max_so_far < max_ending_here)
max_so_far = max_ending_here
if (max_ending_here < 0)
max_ending_here = 0
}
return max_so_far
}
// Driver code
var a = [ -2, -3, 4, -1, -2, 1, 5, -3 ]
document.write("Maximum contiguous sum is",
maxSubArraySum(a, a.length))
// This code is contributed by AnkThon
</script>
C++
int maxSubarraySum(int arr[], int size)
{
int max_ending_here = 0, max_so_far = INT_MIN;
for (int i = 0; i < size; i++) {
// include current element to previous subarray only
// when it can add to a bigger number than itself.
if (arr[i] <= max_ending_here + arr[i]) {
max_ending_here += arr[i];
}
// Else start the max subarray from current element
else {
max_ending_here = arr[i];
}
if (max_ending_here > max_so_far)
max_so_far = max_ending_here;
}
return max_so_far;
} // contributed by Vipul Raj
Java
static int maxSubArraySum(int a[],int size)
{
int max_so_far = a[0], max_ending_here = 0;
for (int i = 0; i < size; i++)
{
max_ending_here = max_ending_here + a[i];
if (max_ending_here < 0)
max_ending_here = 0;
/* Do not compare for all
elements. Compare only
when max_ending_here > 0 */
else if (max_so_far < max_ending_here)
max_so_far = max_ending_here;
}
return max_so_far;
}
// This code is contributed by ANKITRAI1
Python
def maxSubArraySum(a,size): max_so_far = a[0] max_ending_here = 0 for i in range(0, size): max_ending_here = max_ending_here + a[i] if max_ending_here < 0: max_ending_here = 0 # Do not compare for all elements. Compare only # when max_ending_here > 0 elif (max_so_far < max_ending_here): max_so_far = max_ending_here return max_so_far
C#
static int maxSubArraySum(int[] a, int size)
{
int max_so_far = a[0], max_ending_here = 0;
for (int i = 0; i < size; i++) {
max_ending_here = max_ending_here + a[i];
if (max_ending_here < 0)
max_ending_here = 0;
/* Do not compare for all
elements. Compare only
when max_ending_here > 0 */
else if (max_so_far < max_ending_here)
max_so_far = max_ending_here;
}
return max_so_far;
}
// This code is contributed
// by ChitraNayal
PHP
<?php
function maxSubArraySum(&$a, $size)
{
$max_so_far = $a[0];
$max_ending_here = 0;
for ($i = 0; $i < $size; $i++)
{
$max_ending_here = $max_ending_here + $a[$i];
if ($max_ending_here < 0)
$max_ending_here = 0;
/* Do not compare for all elements.
Compare only when max_ending_here > 0 */
else if ($max_so_far < $max_ending_here)
$max_so_far = $max_ending_here;
}
return $max_so_far;
// This code is contributed
// by ChitraNayal
?>
Javascript
<script>
// JavaScript Program to implement
// the above approach
function maxSubarraySum(arr, size)
{
let max_ending_here = 0, max_so_far = Number.MIN_VALUE;
for (let i = 0; i < size; i++) {
// include current element to previous subarray only
// when it can add to a bigger number than itself.
if (arr[i] <= max_ending_here + arr[i]) {
max_ending_here += arr[i];
}
// Else start the max subarray from current element
else {
max_ending_here = arr[i];
}
if (max_ending_here > max_so_far) {
max_so_far = max_ending_here;
}
}
return max_so_far;
}
// This code is contributed by Potta Lokesh
</script>
C++
#include<iostream>
using namespace std;
int maxSubArraySum(int a[], int size)
{
int max_so_far = a[0];
int curr_max = a[0];
for (int i = 1; i < size; i++)
{
curr_max = max(a[i], curr_max+a[i]);
max_so_far = max(max_so_far, curr_max);
}
return max_so_far;
}
/* Driver program to test maxSubArraySum */
int main()
{
int a[] = {-2, -3, 4, -1, -2, 1, 5, -3};
int n = sizeof(a)/sizeof(a[0]);
int max_sum = maxSubArraySum(a, n);
cout << "Maximum contiguous sum is " << max_sum;
return 0;
}
Java
// Java program to print largest contiguous
// array sum
import java.io.*;
class GFG {
static int maxSubArraySum(int a[], int size)
{
int max_so_far = a[0];
int curr_max = a[0];
for (int i = 1; i < size; i++)
{
curr_max = Math.max(a[i], curr_max+a[i]);
max_so_far = Math.max(max_so_far, curr_max);
}
return max_so_far;
}
/* Driver program to test maxSubArraySum */
public static void main(String[] args)
{
int a[] = {-2, -3, 4, -1, -2, 1, 5, -3};
int n = a.length;
int max_sum = maxSubArraySum(a, n);
System.out.println("Maximum contiguous sum is "
+ max_sum);
}
}
// This code is contributed by Prerna Saini
Python
# Python program to find maximum contiguous subarray def maxSubArraySum(a,size): max_so_far =a[0] curr_max = a[0] for i in range(1,size): curr_max = max(a[i], curr_max + a[i]) max_so_far = max(max_so_far,curr_max) return max_so_far # Driver function to check the above function a = [-2, -3, 4, -1, -2, 1, 5, -3] print"Maximum contiguous sum is" , maxSubArraySum(a,len(a)) #This code is contributed by _Devesh Agrawal_
C#
// C# program to print largest
// contiguous array sum
using System;
class GFG
{
static int maxSubArraySum(int []a, int size)
{
int max_so_far = a[0];
int curr_max = a[0];
for (int i = 1; i < size; i++)
{
curr_max = Math.Max(a[i], curr_max+a[i]);
max_so_far = Math.Max(max_so_far, curr_max);
}
return max_so_far;
}
// Driver code
public static void Main ()
{
int []a = {-2, -3, 4, -1, -2, 1, 5, -3};
int n = a.Length;
Console.Write("Maximum contiguous sum is "
+ maxSubArraySum(a, n));
}
}
// This code is contributed by Sam007_
PHP
<?php
function maxSubArraySum($a, $size)
{
$max_so_far = $a[0];
$curr_max = $a[0];
for ($i = 1; $i < $size; $i++)
{
$curr_max = max($a[$i],
$curr_max + $a[$i]);
$max_so_far = max($max_so_far,
$curr_max);
}
return $max_so_far;
}
// Driver Code
$a = array(-2, -3, 4, -1,
-2, 1, 5, -3);
$n = sizeof($a);
$max_sum = maxSubArraySum($a, $n);
echo "Maximum contiguous sum is " .
$max_sum;
// This code is contributed
// by Akanksha Rai(Abby_akku)
?>
Javascript
<script>
// C# program to print largest
// contiguous array sum
function maxSubArraySum(a,size)
{
let max_so_far = a[0];
let curr_max = a[0];
for (let i = 1; i < size; i++)
{
curr_max = Math.max(a[i], curr_max+a[i]);
max_so_far = Math.max(max_so_far, curr_max);
}
return max_so_far;
}
// Driver code
let a = [-2, -3, 4, -1, -2, 1, 5, -3];
let n = a.length;
document.write("Maximum contiguous sum is ",maxSubArraySum(a, n));
</script>
C++
// C++ program to print largest contiguous array sum
#include<iostream>
#include<climits>
using namespace std;
int maxSubArraySum(int a[], int size)
{
int max_so_far = INT_MIN, max_ending_here = 0,
start =0, end = 0, s=0;
for (int i=0; i< size; i++ )
{
max_ending_here += a[i];
if (max_so_far < max_ending_here)
{
max_so_far = max_ending_here;
start = s;
end = i;
}
if (max_ending_here < 0)
{
max_ending_here = 0;
s = i + 1;
}
}
cout << "Maximum contiguous sum is "
<< max_so_far << endl;
cout << "Starting index "<< start
<< endl << "Ending index "<< end << endl;
}
/*Driver program to test maxSubArraySum*/
int main()
{
int a[] = {-2, -3, 4, -1, -2, 1, 5, -3};
int n = sizeof(a)/sizeof(a[0]);
int max_sum = maxSubArraySum(a, n);
return 0;
}
Java
// Java program to print largest
// contiguous array sum
class GFG {
static void maxSubArraySum(int a[], int size)
{
int max_so_far = Integer.MIN_VALUE,
max_ending_here = 0,start = 0,
end = 0, s = 0;
for (int i = 0; i < size; i++)
{
max_ending_here += a[i];
if (max_so_far < max_ending_here)
{
max_so_far = max_ending_here;
start = s;
end = i;
}
if (max_ending_here < 0)
{
max_ending_here = 0;
s = i + 1;
}
}
System.out.println("Maximum contiguous sum is "
+ max_so_far);
System.out.println("Starting index " + start);
System.out.println("Ending index " + end);
}
// Driver code
public static void main(String[] args)
{
int a[] = { -2, -3, 4, -1, -2, 1, 5, -3 };
int n = a.length;
maxSubArraySum(a, n);
}
}
// This code is contributed by prerna saini
Python3
# Python program to print largest contiguous array sum
from sys import maxsize
# Function to find the maximum contiguous subarray
# and print its starting and end index
def maxSubArraySum(a,size):
max_so_far = -maxsize - 1
max_ending_here = 0
start = 0
end = 0
s = 0
for i in range(0,size):
max_ending_here += a[i]
if max_so_far < max_ending_here:
max_so_far = max_ending_here
start = s
end = i
if max_ending_here < 0:
max_ending_here = 0
s = i+1
print ("Maximum contiguous sum is %d"%(max_so_far))
print ("Starting Index %d"%(start))
print ("Ending Index %d"%(end))
# Driver program to test maxSubArraySum
a = [-2, -3, 4, -1, -2, 1, 5, -3]
maxSubArraySum(a,len(a))
C#
// C# program to print largest
// contiguous array sum
using System;
class GFG
{
static void maxSubArraySum(int []a,
int size)
{
int max_so_far = int.MinValue,
max_ending_here = 0, start = 0,
end = 0, s = 0;
for (int i = 0; i < size; i++)
{
max_ending_here += a[i];
if (max_so_far < max_ending_here)
{
max_so_far = max_ending_here;
start = s;
end = i;
}
if (max_ending_here < 0)
{
max_ending_here = 0;
s = i + 1;
}
}
Console.WriteLine("Maximum contiguous " +
"sum is " + max_so_far);
Console.WriteLine("Starting index " +
start);
Console.WriteLine("Ending index " +
end);
}
// Driver code
public static void Main()
{
int []a = {-2, -3, 4, -1,
-2, 1, 5, -3};
int n = a.Length;
maxSubArraySum(a, n);
}
}
// This code is contributed
// by anuj_67.
PHP
<?php
// PHP program to print largest
// contiguous array sum
function maxSubArraySum($a, $size)
{
$max_so_far = PHP_INT_MIN;
$max_ending_here = 0;
$start = 0;
$end = 0;
$s = 0;
for ($i = 0; $i < $size; $i++)
{
$max_ending_here += $a[$i];
if ($max_so_far < $max_ending_here)
{
$max_so_far = $max_ending_here;
$start = $s;
$end = $i;
}
if ($max_ending_here < 0)
{
$max_ending_here = 0;
$s = $i + 1;
}
}
echo "Maximum contiguous sum is ".
$max_so_far."\n";
echo "Starting index ". $start . "\n".
"Ending index " . $end . "\n";
}
// Driver Code
$a = array(-2, -3, 4, -1, -2, 1, 5, -3);
$n = sizeof($a);
$max_sum = maxSubArraySum($a, $n);
// This code is contributed
// by ChitraNayal
?>
Javascript
<script>
// javascript program to print largest
// contiguous array sum
function maxSubArraySum(a , size) {
var max_so_far = Number.MIN_VALUE, max_ending_here = 0, start = 0, end = 0, s = 0;
for (i = 0; i < size; i++) {
max_ending_here += a[i];
if (max_so_far < max_ending_here) {
max_so_far = max_ending_here;
start = s;
end = i;
}
if (max_ending_here < 0) {
max_ending_here = 0;
s = i + 1;
}
}
document.write("Maximum contiguous sum is " + max_so_far);
document.write("<br/>Starting index " + start);
document.write("<br/>Ending index " + end);
}
// Driver code
var a = [ -2, -3, 4, -1, -2, 1, 5, -3 ];
var n = a.length;
maxSubArraySum(a, n);
// This code is contributed by Rajput-Ji
</script>
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA