Dado un gráfico que representa una red de flujo donde cada borde tiene una capacidad. También dados dos vértices fuente ‘s’ y sumidero ‘t’ en el gráfico, encuentre el flujo máximo posible de s a t con las siguientes restricciones:
- El flujo en un borde no excede la capacidad dada del borde.
- El flujo entrante es igual al flujo saliente para cada vértice excepto s y t.
Por ejemplo, considere el siguiente gráfico del libro CLRS.
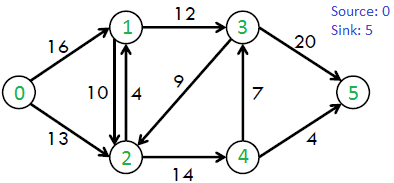
El caudal máximo posible en el gráfico anterior es 23.
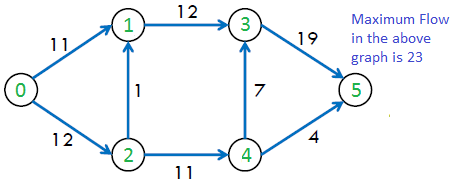
Requisito previo: Introducción al problema de caudal máximo
Algoritmo de Ford-Fulkerson
La siguiente es una idea simple del algoritmo de Ford-Fulkerson:
- Comience con el flujo inicial como 0.
- Si bien hay un camino creciente desde la fuente hasta el sumidero.
- Agregue este flujo de ruta a flujo.
- Flujo de retorno.
Complejidad de tiempo: la complejidad de tiempo del algoritmo anterior es O (max_flow * E). Ejecutamos un ciclo mientras hay una ruta de aumento. En el peor de los casos, podemos agregar 1 unidad de flujo en cada iteración. Por lo tanto, la complejidad del tiempo se convierte en O (max_flow * E).
¿Cómo implementar el algoritmo simple anterior?
Primero definamos el concepto de gráfico residual que se necesita para comprender la implementación.
El gráfico residual de una red de flujo es un gráfico que indica un posible flujo adicional. Si hay una ruta desde la fuente hasta el sumidero en el gráfico residual, entonces es posible agregar flujo. Cada borde de un gráfico residual tiene un valor llamado capacidad residual que es igual a la capacidad original del borde menos el flujo de corriente. La capacidad residual es básicamente la capacidad actual del borde.
Hablemos ahora de los detalles de implementación. La capacidad residual es 0 si no hay borde entre dos vértices del gráfico residual. Podemos inicializar el gráfico residual como gráfico original ya que no hay flujo inicial y la capacidad residual inicialmente es igual a la capacidad original. Para encontrar una ruta de aumento, podemos hacer un BFS o DFS del gráfico residual. Hemos utilizado BFS en la siguiente implementación. Usando BFS, podemos averiguar si hay una ruta desde la fuente hasta el sumidero. BFS también crea una array padre[]. Usando la array parent[], recorremos la ruta encontrada y encontramos el posible flujo a través de esta ruta al encontrar la capacidad residual mínima a lo largo de la ruta. Luego agregamos el flujo de la ruta encontrada al flujo general.
Lo importante es que necesitamos actualizar las capacidades residuales en el gráfico residual. Restamos el flujo de la ruta de todos los bordes a lo largo de la ruta y agregamos el flujo de la ruta a lo largo de los bordes inversos. Necesitamos agregar el flujo de la ruta a lo largo de los bordes inversos porque es posible que más tarde necesitemos enviar el flujo en dirección inversa (consulte el siguiente enlace, por ejemplo).
https://www.geeksforgeeks.org/max-flow-problem-introduction/
A continuación se muestra la implementación del algoritmo Ford-Fulkerson. Para simplificar las cosas, el gráfico se representa como una array 2D.
C++
// C++ program for implementation of Ford Fulkerson
// algorithm
#include <iostream>
#include <limits.h>
#include <queue>
#include <string.h>
using namespace std;
// Number of vertices in given graph
#define V 6
/* Returns true if there is a path from source 's' to sink
't' in residual graph. Also fills parent[] to store the
path */
bool bfs(int rGraph[V][V], int s, int t, int parent[])
{
// Create a visited array and mark all vertices as not
// visited
bool visited[V];
memset(visited, 0, sizeof(visited));
// Create a queue, enqueue source vertex and mark source
// vertex as visited
queue<int> q;
q.push(s);
visited[s] = true;
parent[s] = -1;
// Standard BFS Loop
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v = 0; v < V; v++) {
if (visited[v] == false && rGraph[u][v] > 0) {
// If we find a connection to the sink node,
// then there is no point in BFS anymore We
// just have to set its parent and can return
// true
if (v == t) {
parent[v] = u;
return true;
}
q.push(v);
parent[v] = u;
visited[v] = true;
}
}
}
// We didn't reach sink in BFS starting from source, so
// return false
return false;
}
// Returns the maximum flow from s to t in the given graph
int fordFulkerson(int graph[V][V], int s, int t)
{
int u, v;
// Create a residual graph and fill the residual graph
// with given capacities in the original graph as
// residual capacities in residual graph
int rGraph[V]
[V]; // Residual graph where rGraph[i][j]
// indicates residual capacity of edge
// from i to j (if there is an edge. If
// rGraph[i][j] is 0, then there is not)
for (u = 0; u < V; u++)
for (v = 0; v < V; v++)
rGraph[u][v] = graph[u][v];
int parent[V]; // This array is filled by BFS and to
// store path
int max_flow = 0; // There is no flow initially
// Augment the flow while there is path from source to
// sink
while (bfs(rGraph, s, t, parent)) {
// Find minimum residual capacity of the edges along
// the path filled by BFS. Or we can say find the
// maximum flow through the path found.
int path_flow = INT_MAX;
for (v = t; v != s; v = parent[v]) {
u = parent[v];
path_flow = min(path_flow, rGraph[u][v]);
}
// update residual capacities of the edges and
// reverse edges along the path
for (v = t; v != s; v = parent[v]) {
u = parent[v];
rGraph[u][v] -= path_flow;
rGraph[v][u] += path_flow;
}
// Add path flow to overall flow
max_flow += path_flow;
}
// Return the overall flow
return max_flow;
}
// Driver program to test above functions
int main()
{
// Let us create a graph shown in the above example
int graph[V][V]
= { { 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 },
{ 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 },
{ 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 } };
cout << "The maximum possible flow is "
<< fordFulkerson(graph, 0, 5);
return 0;
}
Java
// Java program for implementation of Ford Fulkerson
// algorithm
import java.io.*;
import java.lang.*;
import java.util.*;
import java.util.LinkedList;
class MaxFlow {
static final int V = 6; // Number of vertices in graph
/* Returns true if there is a path from source 's' to
sink 't' in residual graph. Also fills parent[] to
store the path */
boolean bfs(int rGraph[][], int s, int t, int parent[])
{
// Create a visited array and mark all vertices as
// not visited
boolean visited[] = new boolean[V];
for (int i = 0; i < V; ++i)
visited[i] = false;
// Create a queue, enqueue source vertex and mark
// source vertex as visited
LinkedList<Integer> queue
= new LinkedList<Integer>();
queue.add(s);
visited[s] = true;
parent[s] = -1;
// Standard BFS Loop
while (queue.size() != 0) {
int u = queue.poll();
for (int v = 0; v < V; v++) {
if (visited[v] == false
&& rGraph[u][v] > 0) {
// If we find a connection to the sink
// node, then there is no point in BFS
// anymore We just have to set its parent
// and can return true
if (v == t) {
parent[v] = u;
return true;
}
queue.add(v);
parent[v] = u;
visited[v] = true;
}
}
}
// We didn't reach sink in BFS starting from source,
// so return false
return false;
}
// Returns the maximum flow from s to t in the given
// graph
int fordFulkerson(int graph[][], int s, int t)
{
int u, v;
// Create a residual graph and fill the residual
// graph with given capacities in the original graph
// as residual capacities in residual graph
// Residual graph where rGraph[i][j] indicates
// residual capacity of edge from i to j (if there
// is an edge. If rGraph[i][j] is 0, then there is
// not)
int rGraph[][] = new int[V][V];
for (u = 0; u < V; u++)
for (v = 0; v < V; v++)
rGraph[u][v] = graph[u][v];
// This array is filled by BFS and to store path
int parent[] = new int[V];
int max_flow = 0; // There is no flow initially
// Augment the flow while there is path from source
// to sink
while (bfs(rGraph, s, t, parent)) {
// Find minimum residual capacity of the edhes
// along the path filled by BFS. Or we can say
// find the maximum flow through the path found.
int path_flow = Integer.MAX_VALUE;
for (v = t; v != s; v = parent[v]) {
u = parent[v];
path_flow
= Math.min(path_flow, rGraph[u][v]);
}
// update residual capacities of the edges and
// reverse edges along the path
for (v = t; v != s; v = parent[v]) {
u = parent[v];
rGraph[u][v] -= path_flow;
rGraph[v][u] += path_flow;
}
// Add path flow to overall flow
max_flow += path_flow;
}
// Return the overall flow
return max_flow;
}
// Driver program to test above functions
public static void main(String[] args)
throws java.lang.Exception
{
// Let us create a graph shown in the above example
int graph[][] = new int[][] {
{ 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 },
{ 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 },
{ 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 }
};
MaxFlow m = new MaxFlow();
System.out.println("The maximum possible flow is "
+ m.fordFulkerson(graph, 0, 5));
}
}
Python
# Python program for implementation
# of Ford Fulkerson algorithm
from collections import defaultdict
# This class represents a directed graph
# using adjacency matrix representation
class Graph:
def __init__(self, graph):
self.graph = graph # residual graph
self. ROW = len(graph)
# self.COL = len(gr[0])
'''Returns true if there is a path from source 's' to sink 't' in
residual graph. Also fills parent[] to store the path '''
def BFS(self, s, t, parent):
# Mark all the vertices as not visited
visited = [False]*(self.ROW)
# Create a queue for BFS
queue = []
# Mark the source node as visited and enqueue it
queue.append(s)
visited[s] = True
# Standard BFS Loop
while queue:
# Dequeue a vertex from queue and print it
u = queue.pop(0)
# Get all adjacent vertices of the dequeued vertex u
# If a adjacent has not been visited, then mark it
# visited and enqueue it
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0:
# If we find a connection to the sink node,
# then there is no point in BFS anymore
# We just have to set its parent and can return true
queue.append(ind)
visited[ind] = True
parent[ind] = u
if ind == t:
return True
# We didn't reach sink in BFS starting
# from source, so return false
return False
# Returns the maximum flow from s to t in the given graph
def FordFulkerson(self, source, sink):
# This array is filled by BFS and to store path
parent = [-1]*(self.ROW)
max_flow = 0 # There is no flow initially
# Augment the flow while there is path from source to sink
while self.BFS(source, sink, parent) :
# Find minimum residual capacity of the edges along the
# path filled by BFS. Or we can say find the maximum flow
# through the path found.
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min (path_flow, self.graph[parent[s]][s])
s = parent[s]
# Add path flow to overall flow
max_flow += path_flow
# update residual capacities of the edges and reverse edges
# along the path
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
# Create a graph given in the above diagram
graph = [[0, 16, 13, 0, 0, 0],
[0, 0, 10, 12, 0, 0],
[0, 4, 0, 0, 14, 0],
[0, 0, 9, 0, 0, 20],
[0, 0, 0, 7, 0, 4],
[0, 0, 0, 0, 0, 0]]
g = Graph(graph)
source = 0; sink = 5
print ("The maximum possible flow is %d " % g.FordFulkerson(source, sink))
# This code is contributed by Neelam Yadav
C#
// C# program for implementation
// of Ford Fulkerson algorithm
using System;
using System.Collections.Generic;
public class MaxFlow {
static readonly int V = 6; // Number of vertices in
// graph
/* Returns true if there is a path
from source 's' to sink 't' in residual
graph. Also fills parent[] to store the
path */
bool bfs(int[, ] rGraph, int s, int t, int[] parent)
{
// Create a visited array and mark
// all vertices as not visited
bool[] visited = new bool[V];
for (int i = 0; i < V; ++i)
visited[i] = false;
// Create a queue, enqueue source vertex and mark
// source vertex as visited
List<int> queue = new List<int>();
queue.Add(s);
visited[s] = true;
parent[s] = -1;
// Standard BFS Loop
while (queue.Count != 0) {
int u = queue[0];
queue.RemoveAt(0);
for (int v = 0; v < V; v++) {
if (visited[v] == false
&& rGraph[u, v] > 0) {
// If we find a connection to the sink
// node, then there is no point in BFS
// anymore We just have to set its parent
// and can return true
if (v == t) {
parent[v] = u;
return true;
}
queue.Add(v);
parent[v] = u;
visited[v] = true;
}
}
}
// We didn't reach sink in BFS starting from source,
// so return false
return false;
}
// Returns the maximum flow
// from s to t in the given graph
int fordFulkerson(int[, ] graph, int s, int t)
{
int u, v;
// Create a residual graph and fill
// the residual graph with given
// capacities in the original graph as
// residual capacities in residual graph
// Residual graph where rGraph[i,j]
// indicates residual capacity of
// edge from i to j (if there is an
// edge. If rGraph[i,j] is 0, then
// there is not)
int[, ] rGraph = new int[V, V];
for (u = 0; u < V; u++)
for (v = 0; v < V; v++)
rGraph[u, v] = graph[u, v];
// This array is filled by BFS and to store path
int[] parent = new int[V];
int max_flow = 0; // There is no flow initially
// Augment the flow while there is path from source
// to sink
while (bfs(rGraph, s, t, parent)) {
// Find minimum residual capacity of the edhes
// along the path filled by BFS. Or we can say
// find the maximum flow through the path found.
int path_flow = int.MaxValue;
for (v = t; v != s; v = parent[v]) {
u = parent[v];
path_flow
= Math.Min(path_flow, rGraph[u, v]);
}
// update residual capacities of the edges and
// reverse edges along the path
for (v = t; v != s; v = parent[v]) {
u = parent[v];
rGraph[u, v] -= path_flow;
rGraph[v, u] += path_flow;
}
// Add path flow to overall flow
max_flow += path_flow;
}
// Return the overall flow
return max_flow;
}
// Driver code
public static void Main()
{
// Let us create a graph shown in the above example
int[, ] graph = new int[, ] {
{ 0, 16, 13, 0, 0, 0 }, { 0, 0, 10, 12, 0, 0 },
{ 0, 4, 0, 0, 14, 0 }, { 0, 0, 9, 0, 0, 20 },
{ 0, 0, 0, 7, 0, 4 }, { 0, 0, 0, 0, 0, 0 }
};
MaxFlow m = new MaxFlow();
Console.WriteLine("The maximum possible flow is "
+ m.fordFulkerson(graph, 0, 5));
}
}
/* This code contributed by PrinciRaj1992 */
Javascript
<script>
// Javascript program for implementation of Ford
// Fulkerson algorithm
// Number of vertices in graph
let V = 6;
// Returns true if there is a path from source
// 's' to sink 't' in residual graph. Also
// fills parent[] to store the path
function bfs(rGraph, s, t, parent)
{
// Create a visited array and mark all
// vertices as not visited
let visited = new Array(V);
for(let i = 0; i < V; ++i)
visited[i] = false;
// Create a queue, enqueue source vertex
// and mark source vertex as visited
let queue = [];
queue.push(s);
visited[s] = true;
parent[s] = -1;
// Standard BFS Loop
while (queue.length != 0)
{
let u = queue.shift();
for(let v = 0; v < V; v++)
{
if (visited[v] == false &&
rGraph[u][v] > 0)
{
// If we find a connection to the sink
// node, then there is no point in BFS
// anymore We just have to set its parent
// and can return true
if (v == t)
{
parent[v] = u;
return true;
}
queue.push(v);
parent[v] = u;
visited[v] = true;
}
}
}
// We didn't reach sink in BFS starting
// from source, so return false
return false;
}
// Returns the maximum flow from s to t in
// the given graph
function fordFulkerson(graph, s, t)
{
let u, v;
// Create a residual graph and fill the
// residual graph with given capacities
// in the original graph as residual
// capacities in residual graph
// Residual graph where rGraph[i][j]
// indicates residual capacity of edge
// from i to j (if there is an edge.
// If rGraph[i][j] is 0, then there is
// not)
let rGraph = new Array(V);
for(u = 0; u < V; u++)
{
rGraph[u] = new Array(V);
for(v = 0; v < V; v++)
rGraph[u][v] = graph[u][v];
}
// This array is filled by BFS and to store path
let parent = new Array(V);
// There is no flow initially
let max_flow = 0;
// Augment the flow while there
// is path from source to sink
while (bfs(rGraph, s, t, parent))
{
// Find minimum residual capacity of the edhes
// along the path filled by BFS. Or we can say
// find the maximum flow through the path found.
let path_flow = Number.MAX_VALUE;
for(v = t; v != s; v = parent[v])
{
u = parent[v];
path_flow = Math.min(path_flow,
rGraph[u][v]);
}
// Update residual capacities of the edges and
// reverse edges along the path
for(v = t; v != s; v = parent[v])
{
u = parent[v];
rGraph[u][v] -= path_flow;
rGraph[v][u] += path_flow;
}
// Add path flow to overall flow
max_flow += path_flow;
}
// Return the overall flow
return max_flow;
}
// Driver code
// Let us create a graph shown in the above example
let graph = [ [ 0, 16, 13, 0, 0, 0 ],
[ 0, 0, 10, 12, 0, 0 ],
[ 0, 4, 0, 0, 14, 0 ],
[ 0, 0, 9, 0, 0, 20 ],
[ 0, 0, 0, 7, 0, 4 ],
[ 0, 0, 0, 0, 0, 0 ] ];
document.write("The maximum possible flow is " +
fordFulkerson(graph, 0, 5));
// This code is contributed by avanitrachhadiya2155
</script>
The maximum possible flow is 23
La implementación anterior del algoritmo de Ford Fulkerson se llama algoritmo de Edmonds-Karp . La idea de Edmonds-Karp es utilizar BFS en la implementación de Ford Fulkerson, ya que BFS siempre elige un camino con un número mínimo de aristas. Cuando se usa BFS, la complejidad del tiempo en el peor de los casos puede reducirse a O(VE 2 ). La implementación anterior utiliza una representación de array de adyacencia, aunque donde BFS toma el tiempo O(V 2 ), la complejidad temporal de la implementación anterior es O(EV 3 ) (Consulte el libro CLRS para obtener una prueba de la complejidad temporal)
Este es un problema importante ya que surge en muchas situaciones prácticas. Los ejemplos incluyen, maximizar el transporte con límites de tráfico dados, maximizar el flujo de paquetes en redes informáticas.
Algoritmo de Dinc para Max-Flow.
Ejercicio:
Modifique la implementación anterior para que se ejecute en tiempo O(VE 2 ).
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA