Recomendamos encarecidamente consultar el artículo a continuación antes de pasar a este artículo.
Algoritmo Push Relabel | Conjunto 1 (Introducción e Ilustración)
Planteamiento del problema:
Dado un gráfico que representa una red de flujo donde cada borde tiene una capacidad. También dados dos vértices fuente ‘s’ y sumidero ‘t’ en el gráfico, encuentre el flujo máximo posible de s a t con las siguientes restricciones:
- El flujo en un borde no excede la capacidad dada del borde.
- El flujo entrante es igual al flujo saliente para cada vértice excepto s y t.
Por ejemplo, considere el siguiente gráfico del libro CLRS.
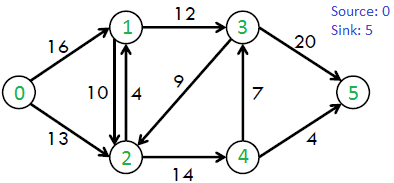
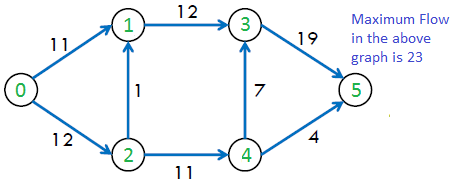
El caudal máximo posible en el gráfico anterior es 23.
Push-Relabel Algorithm
1) Initialize PreFlow : Initialize Flows and Heights
2) While it is possible to perform a Push() or Relabel() on a vertex
// Or while there is a vertex that has excess flow
Do Push() or Relabel()
// At this point all vertices have Excess Flow as 0 (Except source
// and sink)
3) Return flow.
A continuación se muestran las principales operaciones realizadas en el algoritmo Push Relabel.
Hay tres operaciones principales en el algoritmo Push-Relabel
1. Initialize PreFlow() Inicializa alturas y flujos de todos los vértices.
Preflow() 1) Initialize height and flow of every vertex as 0. 2) Initialize height of source vertex equal to total number of vertices in graph. 3) Initialize flow of every edge as 0. 4) For all vertices adjacent to source s, flow and excess flow is equal to capacity initially.
2. Push() se usa para hacer que el flujo fluya desde un Node que tiene exceso de flujo. Si un vértice tiene exceso de flujo y hay un adyacente con menor altura (en el gráfico residual), empujamos el flujo del vértice al adyacente con menor altura. La cantidad de flujo empujado a través de la tubería (borde) es igual al mínimo de exceso de flujo y capacidad del borde.
3. La operación Relabel() se usa cuando un vértice tiene exceso de flujo y ninguno de sus adyacentes está a la altura más baja. Básicamente, aumentamos la altura del vértice para que podamos realizar push(). Para aumentar la altura, elegimos la altura mínima adyacente (en el gráfico residual, es decir, un adyacente al que podemos agregar flujo) y le sumamos 1.
Implementación:
La siguiente implementación utiliza la siguiente estructura para representar una red de flujo.
struct Vertex
{
int h; // Height of node
int e_flow; // Excess Flow
}
struct Edge
{
int u, v; // Edge is from u to v
int flow; // Current flow
int capacity;
}
class Graph
{
Edge edge[]; // Array of edges
Vertex ver[]; // Array of vertices
}
El siguiente código usa el gráfico dado como una red de flujo y un gráfico residual. No hemos creado un gráfico separado para el gráfico residual y hemos usado el mismo gráfico por simplicidad.
Implementación:
C++
// C++ program to implement push-relabel algorithm for
// getting maximum flow of graph
#include <bits/stdc++.h>
using namespace std;
struct Edge
{
// To store current flow and capacity of edge
int flow, capacity;
// An edge u--->v has start vertex as u and end
// vertex as v.
int u, v;
Edge(int flow, int capacity, int u, int v)
{
this->flow = flow;
this->capacity = capacity;
this->u = u;
this->v = v;
}
};
// Represent a Vertex
struct Vertex
{
int h, e_flow;
Vertex(int h, int e_flow)
{
this->h = h;
this->e_flow = e_flow;
}
};
// To represent a flow network
class Graph
{
int V; // No. of vertices
vector<Vertex> ver;
vector<Edge> edge;
// Function to push excess flow from u
bool push(int u);
// Function to relabel a vertex u
void relabel(int u);
// This function is called to initialize
// preflow
void preflow(int s);
// Function to reverse edge
void updateReverseEdgeFlow(int i, int flow);
public:
Graph(int V); // Constructor
// function to add an edge to graph
void addEdge(int u, int v, int w);
// returns maximum flow from s to t
int getMaxFlow(int s, int t);
};
Graph::Graph(int V)
{
this->V = V;
// all vertices are initialized with 0 height
// and 0 excess flow
for (int i = 0; i < V; i++)
ver.push_back(Vertex(0, 0));
}
void Graph::addEdge(int u, int v, int capacity)
{
// flow is initialized with 0 for all edge
edge.push_back(Edge(0, capacity, u, v));
}
void Graph::preflow(int s)
{
// Making h of source Vertex equal to no. of vertices
// Height of other vertices is 0.
ver[s].h = ver.size();
//
for (int i = 0; i < edge.size(); i++)
{
// If current edge goes from source
if (edge[i].u == s)
{
// Flow is equal to capacity
edge[i].flow = edge[i].capacity;
// Initialize excess flow for adjacent v
ver[edge[i].v].e_flow += edge[i].flow;
// Add an edge from v to s in residual graph with
// capacity equal to 0
edge.push_back(Edge(-edge[i].flow, 0, edge[i].v, s));
}
}
}
// returns index of overflowing Vertex
int overFlowVertex(vector<Vertex>& ver)
{
for (int i = 1; i < ver.size() - 1; i++)
if (ver[i].e_flow > 0)
return i;
// -1 if no overflowing Vertex
return -1;
}
// Update reverse flow for flow added on ith Edge
void Graph::updateReverseEdgeFlow(int i, int flow)
{
int u = edge[i].v, v = edge[i].u;
for (int j = 0; j < edge.size(); j++)
{
if (edge[j].v == v && edge[j].u == u)
{
edge[j].flow -= flow;
return;
}
}
// adding reverse Edge in residual graph
Edge e = Edge(0, flow, u, v);
edge.push_back(e);
}
// To push flow from overflowing vertex u
bool Graph::push(int u)
{
// Traverse through all edges to find an adjacent (of u)
// to which flow can be pushed
for (int i = 0; i < edge.size(); i++)
{
// Checks u of current edge is same as given
// overflowing vertex
if (edge[i].u == u)
{
// if flow is equal to capacity then no push
// is possible
if (edge[i].flow == edge[i].capacity)
continue;
// Push is only possible if height of adjacent
// is smaller than height of overflowing vertex
if (ver[u].h > ver[edge[i].v].h)
{
// Flow to be pushed is equal to minimum of
// remaining flow on edge and excess flow.
int flow = min(edge[i].capacity - edge[i].flow,
ver[u].e_flow);
// Reduce excess flow for overflowing vertex
ver[u].e_flow -= flow;
// Increase excess flow for adjacent
ver[edge[i].v].e_flow += flow;
// Add residual flow (With capacity 0 and negative
// flow)
edge[i].flow += flow;
updateReverseEdgeFlow(i, flow);
return true;
}
}
}
return false;
}
// function to relabel vertex u
void Graph::relabel(int u)
{
// Initialize minimum height of an adjacent
int mh = INT_MAX;
// Find the adjacent with minimum height
for (int i = 0; i < edge.size(); i++)
{
if (edge[i].u == u)
{
// if flow is equal to capacity then no
// relabeling
if (edge[i].flow == edge[i].capacity)
continue;
// Update minimum height
if (ver[edge[i].v].h < mh)
{
mh = ver[edge[i].v].h;
// updating height of u
ver[u].h = mh + 1;
}
}
}
}
// main function for printing maximum flow of graph
int Graph::getMaxFlow(int s, int t)
{
preflow(s);
// loop until none of the Vertex is in overflow
while (overFlowVertex(ver) != -1)
{
int u = overFlowVertex(ver);
if (!push(u))
relabel(u);
}
// ver.back() returns last Vertex, whose
// e_flow will be final maximum flow
return ver.back().e_flow;
}
// Driver program to test above functions
int main()
{
int V = 6;
Graph g(V);
// Creating above shown flow network
g.addEdge(0, 1, 16);
g.addEdge(0, 2, 13);
g.addEdge(1, 2, 10);
g.addEdge(2, 1, 4);
g.addEdge(1, 3, 12);
g.addEdge(2, 4, 14);
g.addEdge(3, 2, 9);
g.addEdge(3, 5, 20);
g.addEdge(4, 3, 7);
g.addEdge(4, 5, 4);
// Initialize source and sink
int s = 0, t = 5;
cout << "Maximum flow is " << g.getMaxFlow(s, t);
return 0;
}
Maximum flow is 23
El código de este artículo es una contribución de Siddharth Lalwani y Utkarsh Trivedi .
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA