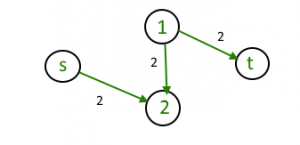
Los problemas de flujo máximo implican encontrar un flujo factible a través de una red de flujo de fuente única y sumidero único que sea máximo.
Tomemos una imagen para explicar cómo quiere decir la definición anterior.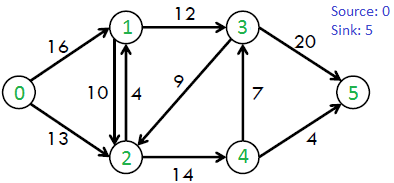
Cada borde está etiquetado con capacidad, la cantidad máxima de cosas que puede transportar. El objetivo es averiguar cuántas cosas se pueden empujar desde el vértice s (fuente) al vértice t (sumidero).
. el caudal máximo posible es: 23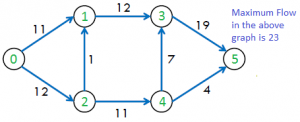
Los siguientes son diferentes enfoques para resolver el problema:
1. Enfoque de algoritmo codicioso ingenuo (puede que no produzca un resultado óptimo o correcto)
El enfoque codicioso del problema de flujo máximo es comenzar con el flujo cero y producir flujos con avidez con un valor cada vez mayor. La forma natural de proceder de uno a otro es enviar más flujo en algún camino de s a t.
Cómo funciona el enfoque de Greedy para encontrar el flujo máximo:
E number of edge
f(e) flow of edge
C(e) capacity of edge
1) Initialize : max_flow = 0
f(e) = 0 for every edge 'e' in E
2) Repeat search for an s-t path P while it exists.
a) Find if there is a path from s to t using BFS
or DFS. A path exists if f(e) < C(e) for
every edge e on the path.
b) If no path found, return max_flow.
c) Else find minimum edge value for path P
// Our flow is limited by least remaining
// capacity edge on path P.
(i) flow = min(C(e)- f(e)) for path P ]
max_flow += flow
(ii) For all edge e of path increment flow
f(e) += flow
3) Return max_flow
Tenga en cuenta que la búsqueda de ruta solo necesita determinar si hay o no una ruta st en el subgrafo de aristas e con f(e) < C(e). Esto se hace fácilmente en tiempo lineal usando BFS o DFS.
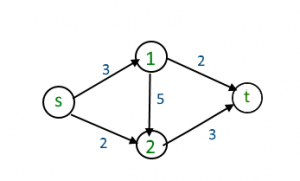
Hay una ruta desde la fuente (s) hasta el fregadero (t) [ s -> 1 -> 2 -> t] con un flujo máximo de 3 unidades (la ruta se muestra en color azul) Después de eliminar todos los bordes inútiles del gráfico, se ve como arriba En el gráfico, no hay un camino desde la fuente hasta el sumidero, por lo que el flujo máximo es de 3 unidades. Pero el flujo máximo es de 5 unidades. para superar este problema usamos gráfico residual.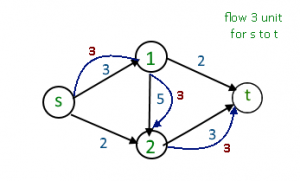
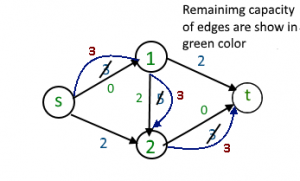
2. Gráficos de residuos
La idea es extender el ingenuo algoritmo codicioso al permitir operaciones de «deshacer». Por ejemplo, desde el punto donde este algoritmo se atasca en la imagen de arriba, nos gustaría enrutar dos unidades más de flujo a lo largo del borde (s, 2), luego hacia atrás a lo largo del borde (1, 2), deshaciendo 2 de los 3 unidades enrutamos la iteración anterior, y finalmente a lo largo del borde (1,t) borde hacia atrás: (f(e)) y borde hacia adelante: (C(e) – f(e))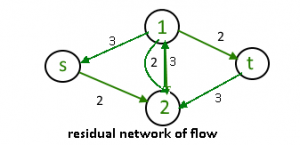
Necesitamos una forma de especificar formalmente las operaciones de «deshacer» permitidas. Esto motiva la siguiente definición simple pero importante, de una red residual. La idea es que, dado un grafo G y un flujo f en él, formamos una nueva red de flujo G f que tiene el mismo conjunto de vértices de G y que tiene dos aristas por cada arista de G. Una arista e = (1, 2) de G que transporta flujo f(e) y tiene capacidad C(e) (para la imagen de arriba) genera un «borde delantero» de G f con capacidad C(e)-f(e) (el espacio restante) y un “borde hacia atrás” (2,1) de G f con capacidad f(e) (la cantidad de flujo previamente enrutado que se puede deshacer). caminos fuente(s)-sumidero(t) con f(e) < C(e) para todos los bordes, según lo buscado por el algoritmo codicioso ingenuo, correspondiente al caso especial de los caminos st de G fque comprenden sólo los bordes delanteros.
Se utiliza la idea de gráfico residual Los algoritmos de Ford-Fulkerson y Dinic
Fuente:
http://theory.stanford.edu/~tim/w16/l/l1.pdf
Este artículo es una contribución de Nishant Singh . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA